3.Определение оптимального размера партии поставки.

Запасы играют как положительную, так и отрицательную роль в деятельности логистической системы. Положительная роль заключается в том, что они обеспечивают непрерывность процессов производства и сбыта продукции, являясь своеобразным буфером, сглаживающим непредвиденные колебания спроса, нарушение сроков поставки ресурсов, повышают надежность логистического менеджмента.

Негативной стороной создания запасов является то, что в них иммобилизуются значительные финансовые средства, которые могли бы быть использованы предприятием на другие цели, например, инвестиции в новые технологии, исследование рынка, улучшение экономических показателей деятельности предприятия. Кроме того, большие уровни запасов готовой продукции препятствуют улучшению ее качества, так как предприятие, прежде всего, заинтересовано в реализации уже имеющейся продукции до вложения инвестиций в повышении ее качества. Исходя из этого, возникает проблема обеспечения непрерывности логистических и технологических процессов при минимальном уровне затрат, связанных с формированием и управлением различными видами запасов в логистической системе.

Один из методов эффективного управления запасами – определение оптимальных партий поставок груза, который позволяет оптимизировать расходы на транспортировку, хранение груза, а также избежать избытка или недостатка груза на складе.

Оптимальный размер партии qопределяется по критерию минимума затрат на транспортировку продукции и хранение запасов.

Величина суммарных затрат рассчитывается по формуле (3.1);

С=+(3.1)

Где – затраты на транспортировку за расчетный период (год), у.е;

– затраты на хранение запаса за расчетный период (год), у.е.

Величина определяется по формуле:

=n*(3.2)

Где n- количество партий, доставляемых за расчетный период,

n= (3.3)

– тариф на перевозку одной партии , у.е./партия.

Затраты на хранение определяются по формуле (3.4):

=*

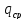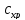
Где qср – средняя величина (в тоннах), которая определяется из предположения, что новая партия завозится после того, как предыдущая полностью израсходована. В этом случае средняя величина рассчитывается по следующей формуле:

*=(3.5)

Подставив выражения ив формулу (3.1), получим:

С=*+*(3.6)

Функция общих затрат С имеет минимум в точке, где ее первая производная по qравна нулю, т.е.

=-*+=0(3.7)

Решив уравнение (3.7) относительно qполучим оптимальный размер партии поставки:

q*=sqr(2Q*/) (3.8)

В качестве размеров годового объема потребления продукции принемаем данные, полученные в результате прогнозирования методом простого среднего: Q=98 тыс. т/год; тариф на перевозку одной партии=80 у.е./т; расходы, связанные с хранением запаса=5 у.е./т.

Подставив данные значения, получим:

q== 1770,9 (т)

При этом общие затраты составляют:

С=*80 +(у.е.)

Решение данной задачи графическим способом заключается в построении графиков зависимости (q),(q) и С(q), предварительно выполнив необходимые расчеты по определению,и С.

Определим значения ,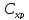и С при измененииqв пределах от 400 до 800 с шагом 100. Результаты расчетов занесем в табл.3.1.

Таблица 3.1

Значения,иС

Размер партии q Затраты, у.е.	400	500	600	700	800
	19600	15680	13066,7	11200	9800
	1000	1250	1500	1750	200
С	20600	16930	14566,7	12950	11800

По данным табл.3.1 построены графики зависимости затрат (транспортных, складских и суммарных) от размера партии (рис.3.1).

Анализ графиков на рис.3.1 показывает, что

Произведем расчет оптимального размера партии в условиях дефицита при величине расходов, связанных с дефицитом 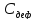=15 у.е/т.

В условиях дефицита значение q*, рассчитанное по формуле (3.8) корректируется на коэффициентk, учитывающий расходы, связанные с дефицитом.

q*=k*(3.9)

Коэффициент kрассчитывают по формуле (3.10):

K=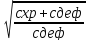(3.10)

– величина расходов, связанных с дефицитом;

Принимаем – =15у.е./т

Подставим значения, получим:

K=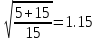

q= 1.15*1770.9= 2036,5 (т)

Из этого следует, что в условиях возможного дефицита размер оптимальной партии поставки необходимо увеличить на 15%.