§ 5. Смешанное произведение векторов

5.1: Определение и геометрический смысл смешанного произведения

Определение: Смешанным произведением трех векторов ,,называется число, равное скалярному произведению векторана векторное произведение векторови, т. е. · ( ) .

Следующая теорема выражает геометрический смысл смешанного произведения.

Теорема: Смешанное произведение векторов · ( )равно объему параллелепипеда построенного на векторах ,,, взятому со знаком « +», если тройка векторов,,– правая, и со знаком « – », если тройка,,– левая. Если же,,компланарны, то · ( ) = 0. Другими словами:

· ( )=

Доказательство. Отложим векторы от общего начала и построим на них параллелепипед. Обозначим и заметим, что .

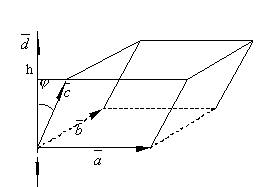
По определению смешанного произведения: .

Предполагая, что и обозначив через h высоту параллелепипеда, находим .Таким образом, при

Если же , то и

Следовательно, .Объединяя оба эти случая, получаем или .

Из доказательства этого свойства в частности следует, что если тройка векторов правая, то смешанное произведение , а если – левая, то .

Докажем второе утверждение. Пусть векторы ,икомпланарны. Если= 0, то, очевидно,· ( ) = 0. Пусть0. Тогда либо  = 0 ( если векторыиколлинеарны ), либо ( ) ( еслиинеколлинеарны). В любом случае· ( ) = 0.

Итак, доказано, что если векторы ,икомпланарны, то· ( ) = 0. Верно и обратное: если· ( ) = 0, то векторы,икомпланарны. Действительно, если бы векторы,ибыли некомпланарны, то по теореме доказанной выше, смешанное произведение· ( ) =V  0, что противоречит условию.

Следствие. Из теоремы легко выводится следующее тождество · ( ) =· ( ) (1) , т. е. знаки · и в смешанном произведении можно менять местами. Действительно, согласно свойству (1) скалярного произведения ( ) ·=· ( ) (2.) . Далее по теореме имеем· ( ) =V, · ( ) =V (3). Так как тройки (,,) и (,,) имеют одинаковую ориентацию, т. е. либо обе правые, либо обе левые, то на основании теоремы в правых частях равенств (3) нужно брать один и тот же знак. Таким образом, имеем· ( )=· ( ) и на основании равенства (2)· ( ) = ( ) ·, т. е. получено тождество (1). В силу тождества (1) смешанные произведения· ( ) и· ( ) можно обозначить более простым символом··.

5.2. Свойства смешанного произведения.

1). Смешанное произведение трех векторов равно нулю, если:

а). Хоть один из перемножаемых векторов равен нулю.

б). Два из перемножаемых векторов коллинеарны.

в). Три ненулевых вектора параллельны одной и той же плоскости.

2). Смешанное произведение не изменится, если в нем поменять местами знаки векторного произведения (×) и скалярного (·) умножения.

3). Смешанное произведение не изменится, если переставлять перемножаемые векторы в круговом порядке ··=··=··

4). При перестановке любых двух векторов смешанное произведение меняет только знак: ··= -··

5). Необходимым и достаточным условием компланарности трех векторов служит условие равенства нулю их смешанного произведения, т. е. ··= 0 .