3.2: Свойства скалярного произведения векторов

Рассмотрим некоторые свойства скалярного произведения векторов:

1. =–(коммутмтивность).

Доказательство: По определению скалярного произведения

=  cos  и

=cos  , но   =  , поскольку это произведение чисел. Следовательно,

= . 

2. ( ) = () – (ассоциативность)

3. (+ ) = + – (дистрибутивность).

Замечание 1: Данное свойство дает право при скалярном умножении векторных многочленов выполнять действия почленно. В силу свойства 1. можно при этом не заботиться о порядке сомножителей, а свойство 2. позволяет объединить числовые коэффициенты векторных сомножителей, например,

(2+5)(3+4) =(2+5)(3) +(2+ 5)(4) =(2)(3) +(5)(3)+(2)(4)+ (5)(4) =6+ 15+ 8+ 20.

4. = ²

Доказательство: По определению скалярного произведения =   cos 0 = ², если  0, т. е. если  0. Если же = 0, то также, по определению, = 0. Но в этом случае = 0 и, значит, равенство = ² также справедливо. 

Скалярное произведение называется скалярным квадратом вектора и обозначается ². На основании только что доказанного мы имеем: ² = ²  отсюда, в частности, = .

5. Если = 0 и 0, то cos  = 0 и  = 2, т.е. векторы иперпендикулярны, т.е. . И обратно, если ,то= 0.

Замечание 2: Для базисных векторов ,,, непосредственно получаем следующие равенства:² = ² =² =1, = = = = = = 0.

3.3. Выражение скалярного произведения через координаты векторов

Теорема: Если векторы изаданы своими координатами:= {Х₁;У₁; Z₁},= {Х₂;У₂; Z₂}, то их скалярное произведение определяется формулой = Х₁ Х₂ +У₁У₂+Z₁Z_{2 .}

Доказательство: Разложим векторы ипо базису , , : =Х₁ + У₁ + Z₁,= Х₂ + У₂ + Z₂. Используя замечание (1), получаем:

= Х₁Х₂²+Х₁У₂+Х₁Z₂+У₁Х₂+У₁У₂ ² + У₁Z₂ + Z₁Х₂+ Z₁У₂ + Z₁Z₂².

Откуда, используя равенства (2), находим: =Х₁Х₂+У₁У₂+Z₁Z_2. 

Из теоремы вытекают два важных следствия.

Следствие 1: Необходимым и достаточным условием перпендикулярности векторов ={Х₁;У₁; Z₁}, и = {Х₂;У₂; Z₂} является равенство: Х₁ Х₂ +У₁У₂+Z₁Z₂=0.

Следствие 2: Угол между векторами = {Х₁;У; Z ₁},= {Х₂;У₂; Z₂} определяется равенством:

Cos φ=

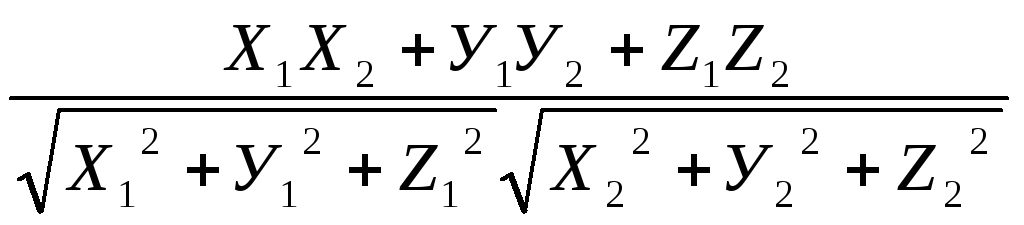
Действительно, по определению скалярного произведения =  cos , где   угол, откуда cos  = . Пример: Даны три точки А (11 1), В (212), С (2 1 2). Найти угол =  ВАС.

Решение. Применяя терему доказанную выше, найдем = 110, = 101. Отсюда на основании следствия (2) получаем: cos = = .

Следовательно,  = 60⁰.

3.4. Деление отрезка в данном отношении

Пусть в пространстве задан произвольный отрезок М₁М₂ и точка М – любая точка этого отрезка, отличная от М₂. Пусть число называемое отношением, в котором точка М делит отрезок М₁М_{2. .} Задача о делении отрезка в данном отношении  состоит в том, чтобы по данному отношению и данным координатам точек М₁ и М₂ найти координаты точки М. Решить эту задачу позволяет следующая теорема:

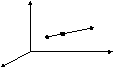
Теорема: Если точка М (х; у; z) делит отрезок М₁М₂ в отношении , то координаты этой точки определяются по формулам:

Х= у =z =

z

М М ₂

М ₁

у

х О

Доказательство: По теореме о пропорциональности отрезков (из элементарной геометрии), заключенными между параллельными прямыми, имеем:

, но ,,т. к. хх₁ и х₂  х, имеем х=. Аналогично доказываются формулы у =z = .

Следствие: Если М₁(х₁; у₁; z₁) и М₂ (х ₂; у ₂; z ₂) – концы отрезка М₁М₂ , а точка М (х; у; z) – середина этого отрезка, то ее координаты находятся по формулам:

Х = у = , z = . (*)

Пример. Даны точки М ₁ (1;1) и М ₂(7;4). Найти точку М (х; у), которая в два раза ближе к М ₁, чем М ₂.

Решение: Искомая точка М делит отрезок М₁М₂ в отношении  =12. Применяя формулы (*), находим координаты этой точки: х=3, у=2.