1.6: Направляющие косинусы вектора

Пусть дан произвольный вектор = будем считать, что выходит из начала координат и не лежит ни в одной координатной плоскости. Проведем через точку М плоскости, перпендикулярные осям. Вместе с координатными плоскостями они образуют прямоугольный параллелепипед диагональю которого служит отрезок ОМ

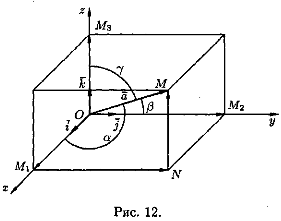
Из элементарной геометрии известно, что квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его измерений. Следовательно,

ОМ² = ОМ₁² +  ОМ₂² + ОМ₃².

Но ОМ =, =Х, =У, =Z таким образом, получаем ,(3).

Обозначим через α, β, γ углы вектор аи осями координат. Из формул (1), (2) и (3) получаем

cosα = , cos β = , cos γ = 

cosα, cosβ, cosγ называются направляющими косинусами вектора .

Возводя в квадрат левую и правую части каждого из равенств, и суммируя полученные результаты, имеем:

сos² + cos ² +cos²  = 1, т.е. сумма квадратов направляющих косинусов любого вектора равна единице.

В заключении пункта рассмотрим задачу:

Пусть даны две произвольные точки М₁ (х_1у_1z₁ ), М₂(х_2у_2z₂ ). Найдем расстояние d между ними. Используя теорему 2, и формулу (3), сразу получаем искомый результат:

= х ₂ – х у₂ –у ₁ z₂ –z ₁ , а так как d – длина вектора , тоd =  = – формула расстояния между двумя точками, заданными своими координатами.

­

§2 . Разложение вектора по базису

Определение: Пусть задана система координат Охуz в пространстве. Пусть векторы ,,– единичные векторы осей координат, т. е. =  =  = 1 (т.е. их длины равны единице единичные векторы еще называют орт – векторами), и каждый из них одинаково направлен с соответствующей осью координат. Тройка векторов ,,называетсябазисом.

Имеет место следующая теорема:

Теорема 3: Любой вектор может быть единственным образом разложен по базису,,, т. е. представлен в виде:= + + , где, ,  – некоторые числа.

Доказательство: Приложив вектор к началу координат, обозначим его конец через М (смотри рисунок §1, 1,6.). Проведем через точку М плоскости, перпендикулярные осям координат. Пусть М_1, М_2, М₃ – точки пересечения этих плоскостей с осями координат. По определению сложения векторов имеем:

=+,=+. (1)

Из этого равенства получаем =++. Так как векторыи,и,иколлинеарны, то=,=,=(2), где, ,  – некоторые числа.

Из равенства (1) и соотношений (2) получаем = + + .

Для доказательства единственности этого представления установим, что =Х, =У , =Z , где Х, У, Z – координаты вектора .

Покажем, например, что =Х. Так как Х=, если имеет то же направление, что и вектор, и Х= , если вектор имеет направление, противоположное направлению вектора, то= Х. Сравнивая с равенством=, получаем = Х. Аналогично показывается, что  = У,  = Z . 

§ 3. Скалярное произведение векторов

3.1: Определение скалярного произведения векторов

Определение: Скалярным произведением двух ненулевых векторов и назавается число (скаляр), равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из векторов нулевой, то угол не определен и скалярное произведение по определению полагают равным нулю.

Скалярное произведение векторов и обозначают . Итак, = cos , где   угол между векторами и .



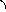
Так как cos  = Пр , cos  = ПР, то можно записать =  Пр = Пр . ( 1 ).

Пр = (2).

Типичным примером скалярного проиведения в физике является формула работы

А =  cos , где

сила, точка приложения которой перемещается из начала в конец вектора