2. Розрахунок резистора складної форми

Розрахунок резистора типу “ меандр ” проводять в такій послідовності.

Визначають ширину резистора по формулах (3)…(5) і округляють отримане значення по формулі (6).

Знаходять довжину середньої лінії меандру

. (10)

Задають відстань між смужками а (див. мал.2). Рекомендується прийняти a=b. Якщо a<a_min, то приймають a=a_min.

Знаходять крок однієї ланки меандру

t = a + b. (11)

Визначають число ланок меандру по наближеній формулі

. (12)

Обчислюють довжину меандру

X = n ∙ (a + b). (13)

Визначають ширину меандру

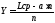. (14)

Перевіряють умову

. (15)

Якщо ця умова виконується, то розрахунок закінчують. Інакше вимагається змінити конструкцію резистора через технологічні обмеження. Для цього змінюють відстань а і перераховують параметри резистора. В даній роботі при невиконанні умови (15) слід збільшити а на величину a_min і повторити обчислення по формулах (11)…(14).

Кінець розрахунку

При необхідності розрахунку декількох резисторів, для кожного з них задаються свої початкові дані (див. табл.1 і табл.2) і виконуються відповідні дії за формулами (1)…(15).

Отже, остаточно загальна частина завдання на курсову роботу формулюється таким чином: розробити алгоритм і програму розрахунку e тонкоплівкових резисторів. Кількість резисторів N задається користувачем разом із іншими початковими даними до розрахунку.

ІНДИВІДУАЛЬНЕ ЗАВДАННЯ

Номер варіанта	Контроль початкових даних		Організація взаємодії з користувачем			Використання масивів								Реалізація фрагмента методики у вигляді підпрограми (функції)
						Розрахунок k-ого резистора в діапазоні значень ρ			Пошук максимального (max) або мінімального (min) розра-хунково-го значення ширини b		Сортування розрахункових значень ширини b за збільшенням (зменшенням)		Введення початкових даних			Розрахункова частина в цілому		Розрахунок коефіцієнта форми kф		Вибір максимального з трьох при розрахунку b і l		Округлення розрахункових значень b і l		Розрахунок резисторів прямокутної форми		Розрахунок резисторів у вигляді меандру
	Візуальний на екрані	Перевірка діапазону	“ Запит-відповідь ”	Меню користувача
					Задані ρ1,…, ρm		Задані ρпоч, ρкін, ∆ρ
1	2	3	4	5	6		7	8		9		10			11		12		13		14		15		16
11	+	-	+	-	+		-	max		-		-			+		1		1		-		0		-

3. Розробка алгоритму рішення задачі

Для представлення алгоритму в даній роботі був використаний графічний спосіб (метод блок-схем). Основна його перевага – це наочність. Блок-схеми наочно показують, як діють керуючі структури. Зображувати алгоритм у вигляді блок-схеми дуже зручно. Вона допомагає записати алгоритм структурно, у такому вигляді його легше зрозуміти і аналізувати.

Проектування алгоритму було проведено зверху вниз, з урахуванням основних принципів структурного програмування: чітка структуризація задачі, розбиття її на послідовність підзадач, реалізація під задач окремими модулями, покрокова деталізація логіки алгоритму, використання типових конструкцій і базових алгоритмічних структур.