
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Уфимский государственный нефтяной технический университет»
Кафедра автоматизации технологических процессов и производств
Курсовой проект
по курсу
«Теория систем»
Вариант 12.
Выполнил: ст.гр. БАТ-11-01 З.А.Нусратуллина
Проверил: ассистент О.И.Гаевская
Уфа 2012
СОДЕРЖАНИЕ
С.
1 Содержание 2
2 Задание 3
2.1 Выделение подсистем на основе некоторой меры 3-10
2.2 Выбор типов шкал 11-12
2.3 Определение порядка проведения работ 13-15
2.4 Построение моделей систем 16
2.5 Анализ иерархий 17-20
3 Заключение 21
4 Список литературы 22
5 Приложения 23-29
ЗАДАНИЯ
2.1 Выделение подсистем на основе некоторой меры
Исходной информацией для выполнения данной части является структура системы в виде взвешенного ориентированного графа (таблица 1).
Таблица 1 –Дуги графа
|
Дуги графа | |||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Исх. Вх. Вес |
1 2 0,4 |
1 3 0,2 |
2 4 0,8 |
3 6 0,9 |
4 1 0,5 |
5 2 0,1 |
5 7 0,6 |
6 3 0,9 |
6 7 0,5 |
7 5 0,8 |
7 3 0,4 |
В таблице 1 обозначено: «Исх.» - начало дуги графа, «Вх.» - конец.
Для заданной системы требуется:
- построить граф системы;
- определить матрицы смежности, инцидентности и контуров;
- определить все элементарные пути из узла х в узел у;
- определить передаточную функцию системы по пути от х=5 к у=7 по формуле Мезона;
- найти определитель системы;
- выделить 2 – 3 несвязных контура как подсистемы и определить их связность;
- рассчитать изменение энтропии системы и вероятности нахождения в каждом из узлов.
Решение
С помощью исходных данных построим граф системы (рисунок 1). Граф – это геометрическая фигура, построенная на множестве вершин и ребер. Определим веса всех возможных путей от входа к выходу системы, где дуги не повторяются:
P1=|V5-V7|=r57=0,6;
P2=|V5-V2-V4-V1-V3-V6-V7|=
=r52*r24*r41*r13*r36*r67=0,1*0,8*0,5*0,2*0,9*0,5=0,0036.
Рисунок 1 – Граф системы
Переделаем рисунок графа системы в более удобный и понятный вариант (рисунок 2):

Рисунок 2 – Грай системы
Дальше построим матрицу смежности, используя граф рисунка (таблица 2):
Таблица 2 – Матрица смежностей
|
|
V1 |
V2 |
V3 |
V4 |
V5 |
V6 |
V7 |
|
V1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
V2 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
V3 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
V4 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
V5 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
V6 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
V7 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
Так же построим матрицу инцидентности (таблица 3):
Таблица 3 – матрица инцидентности
|
|
r12 |
r13 |
r24 |
r36 |
r41 |
r52 |
r57 |
r63 |
r67 |
r73 |
r75 |
|
V1 |
1 |
1 |
|
|
-1 |
|
|
|
|
|
|
|
V2 |
-1 |
|
1 |
|
|
-1 |
|
|
|
|
|
|
V3 |
|
-1 |
|
1 |
|
|
|
-1 |
|
-1 |
|
|
V4 |
|
|
-1 |
|
1 |
|
|
|
|
|
|
|
V5 |
|
|
|
|
|
1 |
1 |
|
|
|
-1 |
|
V6 |
|
|
|
-1 |
|
|
|
1 |
1 |
|
|
|
V7 |
|
|
|
|
|
|
-1 |
|
-1 |
1 |
1 |
Выделим все элементарные контура графа системы и определим их веса:
K1=|V5-V2-V4-V1-V3-V6-V7-V5|=r52*r24*r41*r13*r36*r67*r75=0,1*0,8*0,5*0,2*
*0,9*0,5*0,8=0,00288;
K2=|V7-V5-V7|=r75*r57=0,8*0,6=0,48;
K3=|V2-V4-V1-V2|=r24*r41*r12=0,8*0,5*0,4=0,16;
K4=|V7-V3-V6-V7|=r73*r36*r67=0,4*0,9*0,5=0,18;
K5=|V3-V6-V3|=r36*r63=0,9*0,9=0,81.
Составим матрицу контуров (таблица 4):
Таблица 4 – Матрица контуров
|
|
r12 |
r13 |
r24 |
r36 |
r41 |
r52 |
r57 |
r63 |
r67 |
r73 |
r75 |
|
К1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
К2 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
К3 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
К4 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
К5 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
По формуле Мезона определим эквивалентный оператор, описывающий связь от i-го узла к j-му узлу с учетом всех связей графа:
 экв=
экв= i*
i* i)/
i)/ ,
,
где
 i
– вес i-го
пути от входа к выходу;
i
– вес i-го
пути от входа к выходу;
 i
– минор i-го
пути;
i
– минор i-го
пути;
 - определитель графа.
- определитель графа.
Определитель графа вычисляется по формуле:
 =1-
=1-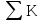 i+
i+ n*
n* m-
m- p*
p* r*
r* l,
l,
где
 i
- сумма
всех контуров;
i
- сумма
всех контуров;
 n*
n*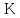 m
сумма произведений пар не касающихся
контуров;
m
сумма произведений пар не касающихся
контуров;
 p*
p* r*
r* l
- сумма
произведений троек не касающихся
контуров.
l
- сумма
произведений троек не касающихся
контуров.
 i
вычисляется по той же формуле, что и
определитель в котором удалены вершины
i-ой
пути.
i
вычисляется по той же формуле, что и
определитель в котором удалены вершины
i-ой
пути.
 =1-(0,00288+0,48+0,16+0,18+0,81)+(
0,48*0,16+0,16*0,18+0,81*0,16+
=1-(0,00288+0,48+0,16+0,18+0,81)+(
0,48*0,16+0,16*0,18+0,81*0,16+
+0,48*0,81)-( 0,48*0,16*0,81)=-0,730064.
После удаления вершин 1-го пути граф будет иметь вид (рисунок 3):

Рисунок 3 – Граф без вершин 1-го пути
 1=1-(
K3+
K5)+(
K3*K5)=1-(0,16+0,81)+
(0,16*0,81)=0,1596.
1=1-(
K3+
K5)+(
K3*K5)=1-(0,16+0,81)+
(0,16*0,81)=0,1596.
После удаления вершин 2-го пути контуров не остается, следовательно минор 2-го равен единице.
 экв=(0,6*0,1596+0,0036*1)/-0,730064=-0,1360977.
экв=(0,6*0,1596+0,0036*1)/-0,730064=-0,1360977.
Расчет энтропии системы.
 H(s)=H0(s)-Hуст(s),
H(s)=H0(s)-Hуст(s),
H(s)= - ∑(Pi*log2Pi),
где Pi - вероятность нахождения системы в том или ином состоянии.
∑Pi =1.
Для расчета изменения энтропии системы через вероятностные состояния используем метод Колмогорова.
Построим структурную схему состояний подсистемы S (рисунок 4).

Рисунок 4- Структурная схема состояний
Для начального состояния:
Р7=Р6=Р5=Р4=Р3=Р2=Р1=1/7;
H0(s)=-1* log2(1/7)= 2,807.
Формула Колмогорова для скорости изменения вероятности нахождения системы в том или ином состоянии:
dPi /dt=Σλj*Pj – Σλi*Pi,
где λ – интенсивность перехода их одного состояния в другое (равна массе соответствующих дуг).
Для каждого состояния системы запишем формулу Колмогорова:
dP1 /dt=λ41*P4 – (λ13+λ12)*P1;
dP2 /dt= λ12*P1+λ52*P5 – λ24*P2;
dP3/dt= λ63*P6+λ13*P1+λ73*P7– λ36*P3;
dP4 /dt=λ24*P2 –λ41*P4;
dP5 /dt=λ75*P7 – (λ52+λ57)*P5;
dP6 /dt=λ36*P3 – (λ63+λ67)*P6;
dP7 /dt= λ57*P5+ λ67*P6 – (λ73+λ75)*P7.
Так как мы считаем установившийся режим, то можно принять, что скорости изменения вероятностей равны нулю. Учитывая то, что сумма всех вероятностей равно единице составим систему:

Решим данную систему в scilab-5.4.0 3 способами, для этого будем вводить матрицу коэффициентов системы в массив A, а вектор правой части системы в массив b.
1 способ: при помощи символа \ :

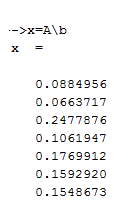
2 способ: методом обратной матрицы:

3 способ - метод Гаусса:

Отсюда получаем:
Р1=0.0884956,
Р2=0.0663717,
Р3=0.2477876,
Р4=0.1061947,
Р5=0.1769912,
Р6=0.1592920,
Р7=0.1548673.
Hуст(s)= - ∑(Pi*log2Pi)= -(0.0884956*log20.0884956+0.0663717*
*log20.0663717+0.2477876*log20.2477876+0.1061947*log20.1061947+
+0.1769912*log20.1769912+0.1592920*log20.1592920+0.1548673*
*log20.1548673=2.69268.
 H(s)=2,807-2.69268=0.11432>0.
H(s)=2,807-2.69268=0.11432>0.
Суммарная энтропия элементов установившегося состояния равна 2.69268, соответственно, изменение энтропии составило 0.11432, и так как энтропия системы больше нуля, то система стремится к порядку.
