Федеральное агентство по образованию

Государственное общеобразовательное учреждение высшего

профессионального образования

Тульский государственный университет

Кафедра «Инструментальные и метрологические системы».

Курсовая работа по дисциплине

Метрология, стандартизация и сертификация.

Вариант №8

Выполнил: студент гр 130501

Cтратилатова Е. О.

Проверил:

Белякова В.А.

Тула 2012

Содержание

Часть 1. Расчет полей допусков размеров детали. 3

Часть 3. Обработка многократных измерений 19

Список литературы: 24

Часть 1. Расчет полей допусков размеров детали.

Задание.

Рассчитать параметры посадки 25; написать все виды обозначения предельных отклонений размеров на конструкторских и рабочих чертежах.

Для расчета дана посадка с зазором в системе отверстия.

1.Отклонения отверстия и вала по ГОСТ 25347-82:

Схема расположения полей допусков посадки

2.Предельные размеры:

3.Допуски отверстия и вала:

либо

4.Зазор:

либо

5.Средний зазор:

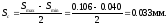
6.Допуск посадки с зазором:

Обозначение предельных отклонений размеров на конструкторских чертежах:

а) условное обозначение полей допусков: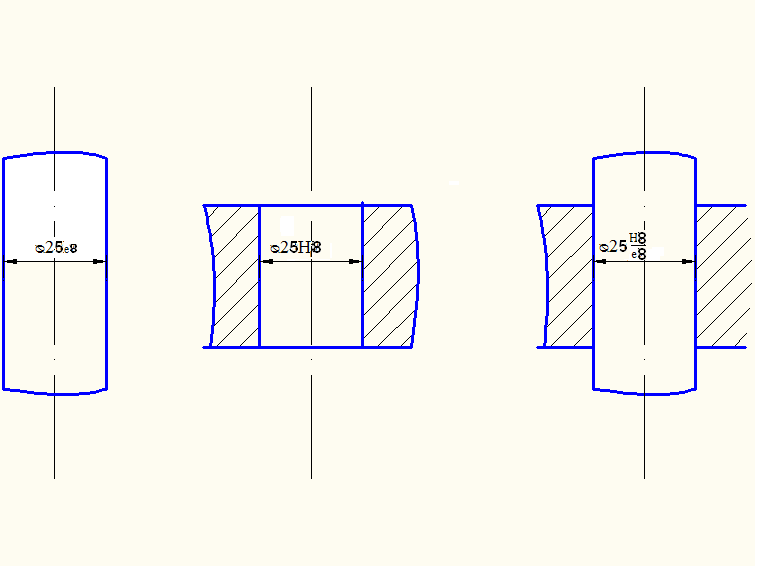б) числовые обозначения предельных отклонений:

в) условное обозначение допусков и числовых значений предельных отклонений:

8.Обозначение размеров на рабочих чертежах:

2. Расчет сборочных размерных цепей.

Задание: По заданным номинальным значениям составляющих размеров и значению замыкающего размера_Δ установить допуски и предельные отклонения составляющих размеров (прямая задача). Проверить правильность назначения допусков и предельных отклонений составляющих размеров (обратная задача). Расчеты провести методом полной взаимозаменяемости и теоретико-вероятностным методом.

NA1	NA2	NA3	NA4	NA5	NA6	АΔ
21	142	21	197	3	16	0 +0.8

Задача №1.1

Назначить допуски и отклонения составляющих размеров с таким расчетом, чтобы обеспечить значение замыкающего размера, равное мм. Расчет произвести методом полной взаимозаменяемости.

На детали, входящие в сборочный комплект, назначены следующие значения номинальных размеров: N₁=21 мм; N₂=142; N₃=21 мм; N₄=197 мм; N₅=3 мм; N₆=16 мм.

1. Согласно заданию:

N_= 0 мм;

Т _ =ES_ – EI_ = (+0.8) – 0 = 0.8 мм;

E_с = (ES_ + EI_)/2 = ((+0.8) + 0)/2 = 0.4 мм;

А_max = N_ + ES_ = 0 + (+0.8) = 0.8 мм;

А_min = N_ + EI_ = 0 +0 = 0 мм.

2. Составим график размерной цепи:

3. Составим уравнение размерной цепи:

A_=

A_ = ₁A₁ + ₂A₂ + ₃A₃ + ₄A₄ + ₅A₅+ ₆A₆.

Значения передаточных отношений

Обозначение передаточных отношений	1	2	3	4	5	6
Численные значения i	-1	-1	-1	+1	+1	-1

4. Проведем проверку правильности назначения номинальных значений составляющих размеров.

N_=

N_= -21-142-21-16+197+3=0;

Так как по условию задачи N_=0, следовательно, номинальные размеры назначены правильно.

5. Осуществим увязку допусков, для чего исходя из величины Т_, рассчитаем допуски составляющих размеров.

Т.к. в узел входят подшипники качения, допуски которых являются заданными, то для определения величины а_с воспользуемся зависимостью:

Допуск ширины подшипников равен 0,12 мм, т.е. Т₁ =Т₃ = 0,12 мм.

Следовательно: ;

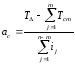а_с = (800 – 2120) / (2,52+2,89+0,73+1,08)  77,56;

6. По приложению А устанавливаем, что такому значению а_с соответствует точность, лежащая между 10 и 11 квалитетами.

Примем для всех размеров 11 квалитет, тогда

T₂ = 0,25 мм; T₄ = 0,29 мм; T₅ = 0,075 мм; T₆ = 0,011 мм.

7. Произведем проверку правильности назначения допусков составляющих размеров по уравнению:

,

= 0,25+0,29+0,075+0,011+0,12+0,12= 0,965 мм.

8. Осуществим увязку средних отклонений, для чего примем следующий характер расположения полей допусков составляющих размеров.

A₁ = A₃=21 _-0,12 ;

A₂ = 142h11(_-0.25);

A₄ = 197JS11(0.145);

A₅ = 3h11(_-0.060);

A₆ =16JS11(0.055);

Сведем данные для расчета в таблицу:

Таблица расчета данных

Обозначение размера	Размер	i	Eci	iEci
А1	21( -0.120)	-1	-0.060	+0.060
А2	142h11(-0.25)	-1	-0.125	+0.125
А3	21( -0.120)	-1	-0.060	+0.060
А4	197JS11(0.145)	+1	0	0
А5	3h11(-0.060)	+1	-0.030	-0.030
А6	16JS11(0.055)	-1	0	0

Из уравнения

найдем среднее отклонение замыкающего размера и сравним его с заданным

E_c = 0.06 + 0.125 + 0.06 - 0.030 = 0.215 мм;

Так как полученное значение не совпадает с заданным, то произведем увязку средних отклонений за счет среднего отклонения размера А₂, принятого в качестве увязочного.

Величину среднего отклонения размера А₂ найдем из уравнения:

+0.4 = +0.060 + 0 +0.060 - Еc`₂ - 0.030 -0

Откуда Еc`₂= -0.031 мм.

Предельные отклонения размера А₂:

ЕS`<sub>2</sub> = Еc`₂ + 0,5Т₂ = -0.031 + 0,50,25= -0.185 мм,

ЕI`<sub>2</sub> = Еc`₂ – 0,5Т₂ = -0.031 – 0,50,25= -0.435 мм.

Таким образом А`₂ = мм

Задача № 1.2 (обратная задача)

Найти предельные значения замыкающего размера А_ при значениях составляющих размеров, полученных в результате решения задачи 1. Расчет произвести методом полной взаимозаменяемости.

Сведем данные для расчета в таблицу

Таблица расчета данных

Обозначение размера	Размер	j	Nj	Ecj	Tj = ES – EI	jNj	jEcj	jTj
А1	21( -0.120)	-1	21	-0.060	0.12	-21	+0.060	0.12
А2		-1	142	-0.31	0.25	-142	+0.31	0.25
А3	21( -0.120)	-1	21	-0.060	0.12	-21	+0.060	0.12
А4	197JS11(0.145)	+1	197	0	0.29	+197	0	0.29
А5	3h11(-0.060)	+1	3	-0.030	0.075	+3	-0.030	0.075
А6	16JS11(0.055)	-1	16	0	0.011	-16	0	0.11

1. Номинальное значение замыкающего размера:

N_=

N_= -21 -142 -21 +197 +3 -16 = 0;

2. Среднее отклонение замыкающего размера:

Е_с = 0.060 +0.31 +0.060 +0 -0.03 +0 = 0.4 мм;

3. Допуск замыкающего размера:

Т_ =0.12 +0.25 +0.12 +0.29 +0.075 +0.11 = 0.965 мм;

4. Предельные отклонения замыкающего размера :

А_max =N_ + Ec_ + 0,5T_= 0 +0.4+0.5*0.965 = 0.882 мм;

А_min = N_ + Ec_ – 0,5T_= 0 +0.4 -0.5*0.965= -0.082 мм;

5. Сравниваем полученные результаты с заданными:

А_{ max расч.} =0.882; А_{max зад.} = 0.8 мм;

А_{min расч.} = -0.082; А_{minзад.} = 0 мм.

Так как условие

не выполняются, следовательно осуществим проверку допусков (А_{ max расч. -} А_{max зад}) / Т_ = (0.882 – 0.8) / 0.965 = 8.49%

(А_{ min зад -} А_{ min расч}) / Т_ = (0 – (0.082) / 0.965 = 8.49%

Значения не превышают 10% => предельные отклонения можно оставить без изменения.