Проверочный расчет передачи

Условие контактной прочности передачи имеет вид _.

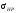Контактные напряжения равны:

=,

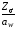
где Z- коэффициент вида передачи Z= 9600

K_Н- коэффициент контактной нагрузки,

K_Н = K_HαK_HβK_НV

Коэффициент неравномерности распределения нагрузки между зубьями:

K_Hα=1+A (n_ст-5)×К_w=1,043

где А=0,06 для прямозубых передач;

K_w- коэффициент, учитывающий приработку зубьев:

K_w= 0,002НВ₂+0,036(V-9)= 0,24

Коэффициент неравномерности распределения нагрузки по ширине колеса_:

K_Hβ=1+(K-1)K_w,

где K- коэффициент распределения нагрузки в начальный период работы, определяемый по табл.9 [1] в зависимости от коэффициента ширины венца по диаметру.

= 0,5(u+1)== 0,6

K= 1,03K_Hβ= 1+(1,03-1)0,195= 1,007

Динамический коэффициент определим потабл.10 [1]:

K_НV=1,092

Окончательно получим:

K_H=1,148

Расчетные контактные напряжения:

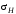= 438,5 МПа

Допускается перегруз по контактным напряжениям не более 5%, рекомендуемый недогруз — до 15%. Расчет перегрузки или недогрузки выполним по формуле:

=100=

Условие контактной прочности выполняется.

Условия изгибной прочности передачи имеют вид _Fj_FPj:

Напряжение изгиба в зубьях шестерни:

,

где Y_Fjкоэффициенты формы зуба;

K_F- коэффициент нагрузки при изгибе;

Напряжение изгиба в зубьях колеса:

Коэффициенты формы зуба:

Y_Fj = 3,47+,

где Z_Vj- эквивалентное число зубьев, для прямозубых передачZ_Vj=Z_j.

Z_V1 = 42Z_V2 =118

Y_F1 =3,47+Y_F2 = 3,47+

Коэффициент нагрузки при изгибе:

K_F=K_FαK_FβK_FV=1×1,025×1,133=1,277

Коэффициент неравномерности распределения нагрузки между зубьями:

K_Fα= 1

Коэффициент неравномерности распределения нагрузки по ширине колеса:

K_Fβ= 0,18+0,82K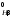= 0,18+0,82= 1,025

Динамический коэффициент при НВ₂ < 350:

K_FV= 1+ 1,5(K_HV-1)=1+ 1,5(1,05-1)= 1,247

Напряжения изгиба:

_F1= 123,7 МПа_FP1= 293,9 МПа

_F2= 128,8 МПа_FP1= 255,8 МПа

Допускается перегруз по напряжениям изгиба не более 5 %, недогруз не регламентируется.

Условия изгибной прочности передачи выполняются, поскольку _F1_FP1и

_F2_FP2.

Силы в зацеплении

Окружная сила F_t== 2,816 кН

Радиальная сила F_r=F_t= 1,025 кН

Расчет тихоходного вала

1. Предварительный расчет вала

Расчет выполняется на кручение по пониженным допускаемым напряжениям [_k]=15 МПа. Ориентировочно определим диаметр вала в опасном сечении, мм

d==мм

где Т– крутящий момент в опасном сечении вала,T= 220,569Нм

Полученное значение округлим до ближайшего числа из ряда на с.5 [2]: d= 50мм

2. Уточненный расчет вала

Наименование опасного сечения –ступенчатый переход с галтелью.

2.1 Определение опорных реакций [см. Приложение 1.]

Горизонтальная плоскость:

R_1Г=R_2Г =кН

Вертикальная плоскость:

R_1В =F_t + F_к -R_2В= 5,24 кН

R_2В =кН

Радиальные опорные реакции:

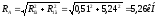
2.2 Моменты и силы в опасном сечении

Суммарный изгибающий момент:

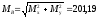Нм

где — изгибающий момент в горизонтальной плоскости,= 201,19Нм;

- изгибающий момент в вертикальной плоскости = 0 Нм.

Осевая сила F_a= 0;

2.3 Геометрические характеристики опасного сечения

Значения площади поперечного сечения A, осевогои полярного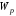моментов сопротивлений для типовых поперечных сечений определяют по формулам.

Для сплошного круглого вала:

A== 19,63,== 12,27,== 24,54;

2.4 Суммарный коэффициент запаса прочности

Определяем по формуле:

S=

где и- коэффициенты запаса прочности по нормальным и касательным напряжениям.

Условие прочности вала имеет вид

S[S]

где [S] - допускаемый коэффициент запаса прочности.

Рекомендуемое значение [S] =2…2.5

Значения и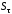определяют по формулам:

=

=

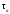где и— пределы выносливости материала при симметричном цикле изгиба и кручения;и— амплитуды напряжений цикла;и- средние напряжения цикла,и— коэффициенты перехода от пределов выносливости образца к пределам выносливости детали,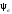и— коэффициенты чувствительности к асимметрии цикла.

Значения иравны:

= 0,02(1+0,01)= 0,18= 0,5= 0,09;

Пределы выносливости материала при симметричном цикле изгиба и кручения определяются по следующим формулам:

для углеродистых сталей

= 0,43=780×0,43 = 335 МПа

= 0,58=0,58×780=195 МПа

При вычислении амплитуд и средних напряжений цикла принимают, что напряжения изгиба меняются по симметричному циклу, а касательные по наиболее неблагоприятному отнулевому циклу. В этом случае:

== 16,394 МПа== 0

==6,479 МПа

Коэффициенты:

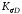= (+K_F-1)/K_V=

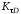= (+K_F-1)/K_V=

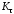где и- эффективные коэффициенты концентрации напряжений

(табл.2…4 [2]); = 3,2= 1,78

и - коэффициенты влияния размера поперечного сечения вала;

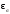== 0,8==0,69

K_F - коэффициент влияния шероховатости поверхности, определяется по табл.5 [2] в зависимости от:

= 3,2 мкм K_F=1,33

K_V- коэффициент влияния упрочнения.

При отсутствии упрочнения поверхности рассчитываемого участка вала принимают K_V=1

В результате расчета получили:

= 4,2 = 2,41

=4,719 =10,04

S== 4,271