Расчет зубчатой передачи

1. Выбор материалов зубчатых колес

Шестерня:

Материал — Сталь 45;

Термическая обработка — улучшение;

Твердость поверхности зуба — 269-302HB;

Колесо:

Материал — Сталь 45;

Термическая обработка — улучшение;

Твердость поверхности зуба — 235-262HB;

2. Определение допускаемых напряжений

2.1 Допускаемые контактные напряжения

_HPj=

где j=1 для шестерни,j=2 для колеса;

_Hlimjпредел контактной выносливости (табл.5 [1]),

_Hlim1= 641 МПа

_Hlim2= 567 МПа

S_Hjкоэффициент безопасности (табл.5 [1]),

S_H1= 1,1

S_H2=1,1

K_HLj- коэффициент долговечности;

K_HLj=1,

здесь N_H0j– базовое число циклов при действии контактных напряжений (табл.4 [1]),

N_H01=

N_H02=

Коэффициент эквивалентности при действии контактных напряжений определим по табл.6 [1] в зависимости от режима нагружения: _h=0,5

Суммарное время работы передачи в часах

t_h= 365×L×24×K_г×К_с×ПВ,

где K_г– коэффициент использования передачи в течение года;

K_с– коэффициент использования передачи в течение суток;

L– срок службы передачи в годах;

ПВ – продолжительность включения;

K_г= 0,7K_с= 0,5L= 6 ПВ= 70%t_h=12877

Суммарное число циклов нагружения:

N_j= 60×n_j×c×t_h,

где с– число зацеплений колеса за один оборот,с= 1;

n_j– частота вращенияj-го колеса,n₁=420,435 мин^-1,n₂= 150,155 мин^-1;

N_1=N_2=

Эквивалентное число циклов контактных напряжений, N_HEj=_hN_Σj;

N_HE1=N_HE2=

Коэффициенты долговечности

K_HL1= 1K_HL2= 1

Допускаемые контактные напряжения для шестерни и колеса

_HP1= 582,7 МПа_HP2= 515,5 МПа

Для прямозубых передач _HP = _HP2

Допускаемые контактные напряжения передачи:

_HP=515,5 МПа

2.2. Допускаемые напряжения изгиба

_FPj=,

где _Flimjпредел выносливости зубьев при изгибе (табл.7 [1]),

_{Flim 1}= 499,6 МПа_{Flim 2}= 434,9 МПа

S_Fjкоэффициент безопасности при изгибе (табл.7 [1]),

S_F1= 1,7S_F2 = 1,7

K_FCjкоэффициент, учитывающий влияние двухстороннего приложения нагрузки, (табл.7 [1])

K_FC1= 1K_FC2= 1

K_FLjкоэффициент долговечности при изгибе:

K_FLj=1

N_F0– базовое число циклов при изгибе;N_F0 = 4×10⁶

N_FEj– эквивалентное число циклов напряжений при изгибе;

N_FEj=_FjN_Σj.

Коэффициент эквивалентности при действии напряжений изгиба определяется по табл.6[1] в зависимости от режима нагружения и способа термообработки

_F= 0,3

N_FE1 = N_FE2 =

K_FL1 = 1 K_FL2 = 1

Допускаемые напряжения изгиба:

_FP1== 293,9 МПа

_FP2== 255,8 МПа

Расчет цилиндрической зубчатой передачи

Межосевое расстояние определяем из условия контактной прочности:

=(u+1),

где - коэффициент вида передачи,= 450

K_Н- коэффициент контактной нагрузки примемK_Н = 1,148

Коэффициент ширины зубчатого венца = 0,3125 (ряд на с.4 [1]).

Расчетное межосевое расстояние = 158,73 мм

Округлим до ближайшего большего стандартного значения (табл.2 [1]) ГОСТ 2185-66=160 мм

Модуль выберем из диапазона

m== 1,6…3,2

Округлим mдо стандартного значения (табл.1 [1]) ГОСТ 9563-60:m=2

Суммарное число зубьев:

Z=,

Z=

Число зубьев шестерни:

Z₁== 42

Число зубьев колеса:

Z₂= Z-Z₁=118

Фактическое передаточное число:

u_ф ==

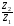Значение u_ф не должно отличаться от номинального более чем на 2.5 % приu4.5 и более чем на 4 % приu > 4.5

u=100= 0,36%

Коэффициенты смещения шестерни и колеса: x₁= 0x₂= 0

Расчетная ширинaвенца колеса:

b_w2== 50 мм

Округляем b_w2 до ближайшего числа из ряда на с.10 [1]:

b_w2 = 50 мм ГОСТ 6636-69

Ширину венца шестерни b_w1примем на 5 мм больше чемb_w2:

b_w1 =55 мм

Определим диаметры окружностей зубчатых колес:

Диаметры делительных окружностей прямозубых колес d_j=mZ_j,

d₁= 84 ммd₂=236 мм

Диаметры окружностей вершин при x=0:d_aj=d_j+2m(1+x_j):

d_a1 =88 мм d_a2 =240 мм

Диаметры окружностей впадин d_fj=d_j-2m(1,25-x_j):

d_f1=79 ммd_f2=231 мм

Вычислим окружную скорость в зацеплении

V== 1,85 м/с

Степень точности передачи выберем по табл.8 [1]: n_ст= 8