Архив2 / курсач docx80 / chernovik_kursach_kristalka

1. Кристаллографическое описание структурной фазы Be.

Элементарная ячейка бериллия - гексагональная примитивная.

Рис.1.1 Гексагональная примитивная ячейка.

1. Структурна решетки кристалла – расположение частиц в пространстве. Тип структуры бериллия – А3.

Группа симметрии, операции которых оставляют хотя бы одну точку пространства на месте, называются точечными группами симметрии. ТГС бериллия - 6/mmm.

Пространственная группа симметрии – совокупность всех возможных операций симметрии кристаллической структуры. ПГС бериллия -

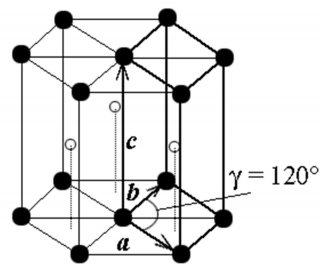
Рис. 1.2. Пространственная гексагональная ячейка

Решетка Бравэ − примитивная, узлы имеют только по вершинам ячейки. Если выбрать один из узлов за начало координат, то все остальные можно получить, повторяя этот атом в пространст­ве периодически с помощью трех трансляций а, b, с.

сингония – гексагональная

Координаты атомов в примитивной ячейке: 0, 0, 0; 2/3, 1/3, 1/2.

Координационное число к.ч. = 12, число атомов в эл. ячейке Z = 2

2. Базис ячейки.

Базис ячейки — совокупность координат узлов, которые задают элементарную кристаллическую ячейку.

Атомы, расположенные в вершинах ячейки, связаны друг с другом трансляциями, а с атомом внутри ячейки— либо осью 6з, либо плоскостью с.

Координаты атомов базиса ячейки: [[000]], [[1/3, 2/3, 1/4]], [[2/3, 1/3, 3/4]].

1.3 Элементы симметрии.

Формула симметрии - L₆6L₂7PC

Класс симметрии- аксиально-центральный. (рис.1.3)

Класс имеет:

а)3 оси симметрии 4-го порядка <100>;[111];[111];[111];[111]

b) 4 оси симметрии 3-го порядка <111>; [111];[111];[111];[111]

c) 6 осей симметрии 2-го порядка <110>; [011],[101],[110],[110],[101],[011]

d) 3 координатные плоскости {100}; (100);(010);(001)

e) 6 диагональных плоскостей {110}; (011); (011);(101);(101);(110);(110)

f) Центр симметрии.

1.4Плотноупакованные плоскости и направления.

Рис.1.3 Плотноупакованные плоскости

(0001)-семейство плотноупакованных плоскостей

<1120>-семейство плотноупакованных направлений

Рис. 1.4 Направления гексагональной плотноупакованной решетки

Порядок плоскостей: АВАВАВАВ

2. Расчет параметров фазы Be.

   1. Радиус атома Be:

   2. Компактность упаковки

Расчет коэффициента упаковки:

3. Радиус координатных сфер и координатные числа

a = d

R1=d

К.Ч.=12

R2=d

К.Ч.=6

R3=1.63d

К.Ч.=6

R4=d

К.Ч.=8

R5=2d

К.Ч=12

3. Кристаллографическое описание Ni₃Al

3.1 Структурный тип: L1₀

Точная группа симметрии: m3m

Пространственная группа симметрии: Im3m

Рис.3.1 Пространственная группа симметрии

Базис элементарной ячейки: (000, ½ ½ 0, ½ 0 ½ , 0 ½ ½ )

3.2 Плотноупакованные плоскости и направления

Рис.3.2 Плотноупакованные плоскости и направления

{110}- семейство плотноупакованных плоскостей

<112>-семейство плотноупакованных направлений

Порядок чередования плоскостей: ABCABC

Минимальный трансляционные вектора: a, b, c; (a+b)/2, (a+c)/2, (b+c)/2

3.3Элементы симметрии – 3L₄4L₃6L₂9PC

а)3 оси симметрии 4-го порядка <100>;[111];[111];[111];[111]

b) 4 оси симметрии 3-го порядка <111>; [111];[111];[111];[111]

c) 6 осей симметрии 2-го порядка <110>; [011],[101],[110],[110],[101],[011]

d) 3 координатные плоскости {100}; (100);(010);(001)

e) 6 диагональных плоскостей {110}; (011); (011);(101);(101);(110);(110)

f) Центр симметрии.

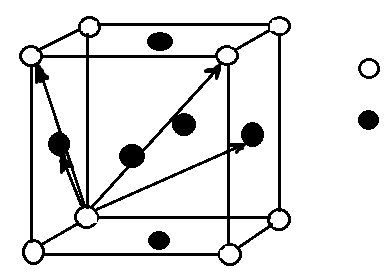
Рис 3.3 Радиусы и координатные числа

R1=d

К.Ч.=12

R2=a

К.Ч.=6

R3= a

К.Ч.=24

R4=2d

К.Ч.=12

R5= d

К.Ч.=8

3.4 Период кристаллической решетки: a=0,375

Рис. 3.4 Семейство плотноупакованных цепочек атома AL

Радиус атома: R=(a)/4=1.325

3.2 Расчет коэффициента упаковки:

3.3 Количество и координаты пор:

4 О-поры: ½ ½ ½ , ½ 00, 0 ½ 0, 00 ½

8 Т-пор (по одной в каждом тетраэдре): ¼ ¼ ¼ , ¼ ¼ ¾ , ¾ ¼ ¼ , ¾ ¼ ¾ , ¼ ¾ ¼ , ¼ ¾ ¾ , ¾ ¾ ¼ , ¾ ¾ ¾