Министерство образования Республики Беларусь

Учреждение образования «Полоцкий государственный университет»

Кафедра радиоэлектроники

Курсовая работа

По курсу:

“Методы анализа и расчёта электронных схем”

Вариант № 6

Выполнил: студент группы 10-Пэл Кожернович Е.А.

Проверил: Мальцев С.В.

Новополоцк 2012

Содержание

Задание и исходные данные……………………………………………..3

1. Расчет выходного сигнала операционным методом………………………………………………………...…………..5

2 Расчет выходного сигнала методом

интеграла Дюамеля …………………………………………………….10

3. Расчёт выходного сигнала частотным методом…………………..13

4. Заключение………………………………………………………………19

Цель работы:

В результате выполнения курсовой работы студент должен:

- изучить физические процессы в линейных цепях в переходном и установившемся режимах;

- приобрести навыки применения основных методов анализа преобразования сигналов линейными цепями;

- приобрести навыки применения дискретного преобразования Фурье (ДПФ) и алгоритма быстрого преобразования Фурье (БПФ) в инженерных расчетах.

1) Задание и исходные данные

Применительно к курсовой работе задача анализа формулируется следующим образом: известны схема исследуемой цепи и входной сигнал u₁(t), требуется определить выходной сигнал u₂(t) и проанализировать зависимость его формы от параметров цепи.

Задачу анализа необходимо решить несколькими методами: операционным методом, методом интеграла Дюамеля (или интеграла свертки) и частотным методом. В выводах по курсовой работе необходимо дать качественное сравнение результатов, полученных при использовании каждого из перечисленных методов.

При расчете выходного сигнала операционным методом необходимо проделать следующее:

1) записать аналитическое выражение для заданного входного сигнала u₁(t) и найти его изображение по Лапласу u₁(P);

2) записать аналитическое выражение передаточной функции цепи К(р);

3) определить изображение u₂(P) выходного сигнала и найти аналитическое выражение оригинала u₂(t);

4) построить временные диаграммы выходного сигнала u₂(t) для трех значений одного из параметров цепи (изменяемый параметр указан в индивидуальном задании).

При расчете выходного сигнала u₂(t) методом интеграла Дюамеля необходимо проделать следующее:

1) записать аналитическое выражение для заданного входного сигнала u₁(t);

2) определить временные характеристики цепи: переходную h(t) и импульсную h_δ(t);

3) рассчитать и построить графики временных характеристик цепи h(t) и h_δ(t) для трех значений изменяемого параметра;

4) методом интеграла Дюамеля определить выходной сигнал (реакцию цепи) u₂(t);

5) построить временные диаграммы сигнала u₂(t) для трех значений изменяемого параметра цепи.

При расчете выходного сигнала частотным методом необходимо проделать следующее:

1) найти спектральную функцию заданного входного сигнала u₁(t), его амплитудно-частотный (АЧС) и фазо-частотный (ФЧС) спектры;

2) определить комплексную частотную характеристику цепи K(jω), найти выражения ее амплитудно-частотной (АЧХ) K(ω) и фазо-частотной (ФЧХ) φ(ω) характеристик;

3) построить графики АЧС и ФЧС сигнала u₁(t), а также АЧХ и ФЧХ цепи для трех значений изменяемого параметра;

4) записать аналитическое выражение спектральной функции выходного сигнала и с помощью обратного ДПФ рассчитать сигнал u₂(t);

5) построить временные диаграммы сигнала для трех значений изменяемого параметра цепи.

Исходные данные:

Параметры цепи						Параметры входных сигналов
Номер схемы	R, Ом	L, мкГ	С, мкФ	Измен.парам.	Номер сигнала		U1, В	U2, В	tи, мкс
6	750		0,02	C	6		9	9	11,25

Ход работы:

Используя среду MatLab построил наш сигнал используя следующий алгоритм:

ti=11.25e-9;

Ui=18;

t=0:(ti/1000):ti;

s=Ui/2+Ui*((sawtooth(2*pi/ti*t,0)-1)/2);

figure;

plot(t,s);

1. Расчет выходного сигнала операционным методом.

Запишем аналитическое выражение для заданного входного сигнала u₁(t) и найдём его изображение по Лапласу u₁(P).

Для этого разобьём наш сигнал на две составляющие:

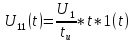
Используя таблицу Лапласа найдём изображение:

Запишем аналитическое выражение передаточной функции цепи К(р).

Для этого преобразуем нашу схему:

Где , , ,

Передаточная функция цепи находится следующим образом:

Подставляя наши значения получим

Подставив исходные данные получим:

определим изображение u₂(P) выходного сигнала и найти аналитическое выражение оригинала u₂(t).

Для этого воспользуемся следующей формулой:

, где

;

Рассчитаем U₁₁(P), U₁₂(P)

Следует иметь в виду, что при нахождении обратного преобразования Лапласа важно помнить, что умножение изображения на e^-pto соответствует запаздыванию оригинала на время t₀.

Рассчитаем

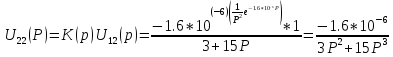
Зная найду

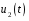
построим временные диаграммы выходного сигнала u₂(t) для трех значений R параметра цепи с шагом 0,1 мкС.

t=0:1*10^(-7):11.25*10^(-7);

t0=5*10^(-6);

S05= 3*10^6*exp((-t)/(2.5*10^(-7)))-exp((-t)/(2.5*10^(-8)));

S1= 3*10^6*exp((-t)/(5*10^(-7)))- exp((-t)/(5*10^(-8)));

S2= 3*10^6*exp((-t)/(10*10^(-7)))- exp((-t)/(10*10^(-8)));

figure; plot (t, S05)

figure; plot (t, S1)

figure; plot (t, S2)

При С=0.01 мкФ

При С=0.02мкФ

При С=0.04мкФ

2. Расчет выходного сигнала методом интеграла Дюамеля

Входной сигнал u₁(t) при анализе линейной цепи методом интеграла Дюамеля удобно представить суммой более простых сигналов так же, как это было сделано ранее:

u₁(t) = u₁₁(t) + u₁₂(t) + u₁₃(t).

+(

Для определения временных характеристик цепи следует воспользоваться уже полученной передаточной функцией К(р), и формулами , ,а также изложенными ранее рекомендациями по вычислению обратного преобразования Лапласа.

Построим временные характеристики

t=0:1*10^(-7):30*10^(-7);

t0=5.75*10^(-6);

S05= exp((-t)/(2.25*10^(-7)));

S1= exp((-t)/(4.5*10^(-7)));

S2= exp((-t)/(9*10^(-7)));

figure; plot (t, S05)

figure; plot (t, S1)

figure; plot (t, S2)

При С=0.01 мкФ

При С=0.02мкФ

При С=0.04мкФ

Методом интеграла Дюамеля определим выходной сигнал (реакцию цепи) u₂(t)

3. Расчёт выходного сигнала частотным методом

найдём спектральную функцию заданного входного сигнала u₁(t), его амплитудно-частотный (АЧС) и фазо-частотный (ФЧС) спектры.

С помощью прямого преобразования Фурье найден спектр заданного сигнала.

ti=11.25e-9;

Ui=18;

t=0:(ti/1000):ti;

s=Ui/2+Ui*((sawtooth(2*pi/ti*t,0)-1)/2);

figure;

plot(t,s);

Y = fft(s);

Yp=fftshift(Y);

a=abs(Yp);

f=-500:1:500;

figure;grid

plot(f(500:600),a(500:600));

Фазо-частотный спектр

R=750;

C=0.02e-6;

dw=2*pi/(3*ti);

wmax=2*pi*18/ti;

w=0:dw:wmax;

Z4=1./(i*w*C);

Z1=R+Z4;

Z3=R;

Z2=R;%

A1=(Z2.*(Z3+Z4))./(Z2+Z3+Z4);

K=(A1./(A1+Z1))*Z4/(Z3+Z4);

y1=abs(K);

Амплитудно-частотная модуляция

i=11.25e-9;

Ui=18;

t=0:(ti/1000):ti;

f1=10^9;

w1=2*pi*f1;

s1=sin(w1*t)

s=s1+(Ui/2+Ui*((sawtooth(2*pi/ti*t,0)-1)/2));

figure;

plot(t,s);

Определяем комплексную частотную характеристику цепи K(jω), находим выражения ее амплитудно-частотной (АЧХ) K(ω) и фазо-частотной (ФЧХ) φ(ω) характеристик;

Амплитудно-частотная характеристика

i=11.25e-9;

Ui=18;

t=0:(ti/1000):ti;

f1=10^7;

w1=2*pi*f1;

s1=0.05*sin(w1*t)

s=s1+(1+0.5*(exp((-t)/(5*10^(-7)))));

figure;

plot(t,s);

Фазо-частотная характеристика

ti=11.25e-6;

Ui=18;

t=0:(ti/1000):ti;

s3=exp((-t)/(5*10^(-7)));

R=750;

C=0.02e-6;

dw=2*pi/(3*ti);

wmax=2*pi*18/ti;

w=0:dw:wmax;

Z2=R;

Z3=R;

Z4=1./(i*w*C);

Z1=Z4+R;

A1=(Z2.*(Z3+Z4))./(Z2+Z3+Z4);

K=(A1./(A1+Z1))*Z4/(Z3+Z4);

y1=abs(K);

figure;

plot(w,y1);

Запишем аналитическое выражение спектральной функции выходного сигнала и с помощью обратного ДПФ рассчитать сигнал u₂(t).

Аналитическое выражение для спектральной функции выходного сигнала определяется произведением коэффициента передачи цепи и спектральной функции входного сигнала, т.е.

.

ti=11.2e-6;

Ui=18;

t=0:(ti/1000):ti;

s=Ui/2+Ui*((sawtooth(2*pi/ti*t,0)-1)/2);

figure;

plot(t(1:1000),s3(1:1000));

Y = fft(s);

Yp=fftshift(Y);

a=abs(Yp)/1000;

f=-500:1:500;

s1 = exp((-t)/(4.5*10^(-7)));

X=s1.*Yp;

plot(t,X)

С помощью обратного ДПФ рассчитаем сигнал u₂(t).

Заключение

В ходе данного курсового проекта, были изучены физические процессы в линейных цепях, в переходном и установившемся режимах. Были изучены различные методы расчёта линейных электрических цепей. Также закреплены и дополнены навыки применения дискретного преобразования Фурье и алгоритма быстрого преобразования Фурье.