
- •2.2. Проверочный расчет зубьев на контактную выносливость
- •2.3. Проверочный расчет зубьев на изгибную прочность
- •2.4. Проверочный расчет зубьев при перегрузке
- •4. Расчет сварного соединения
- •4.1. Техническое задание
- •4.2 Расчет сварного соединения на статическую прочность
- •1. Энергокинематический расчет узла привода
Выбираем межосевое
расстояние
 по ГОСТ
2185-66
по ГОСТ
2185-66
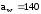 мм [1,c.36].
мм [1,c.36].
Определим модуль передачи по формуле [1, c.36]
 мм,
(2.8)
мм,
(2.8)
где
mn
– модуль передачи, причём
 мм.
мм.
Значение модуля
передачи выбирают из стандартного ряда
[1, c.36].
Выбираем
 мм.
мм.
Суммарное число зубьев в соответствии с [1, c.36] определяют по формуле
 ,
(2.9)
,
(2.9)
где
 – суммарное число зубьев; β – угол
наклона зуба, град.
– суммарное число зубьев; β – угол
наклона зуба, град.
Предварительно
выбираем угол
 = 15º, учитывая,
что передача косозубая, по рекомендации
[1, c.37].
= 15º, учитывая,
что передача косозубая, по рекомендации
[1, c.37].
Подставляя численные значения в формулу (2.9), найдём суммарное число зубьев

Теперь найдём число зубьев шестерни и колеса [1, c.37]
 ,
,
(2.10)
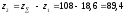 ,
,
где
 – число зубьев на шестерне;
– число зубьев на шестерне; –
число зубьев на колесе.
–
число зубьев на колесе.
Выбираем число
зубьев на шестерне
 ,
а число зубьев на колесе
,
а число зубьев на колесе .
.
Уточним угол
 ,
определив его по формуле
,
определив его по формуле
 (2.11)
(2.11)
Сделаем проверочный расчёт зубьев шестерни на подрезание. Условие работоспособности передачи без подрезания можно записать в виде [1, c.38]
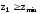 ,
(2.12)
,
(2.12)
где
 –
минимальное число зубьев.
–
минимальное число зубьев.
Для косозубых передач минимальное число зубьев вычисляется по формуле [1, c.38]
 (2.13)
(2.13)
Минимальное число зубьев оказалось меньше, чем фактическое, следовательно, подрезания не произойдет.
Далее определяем делительные диаметры шестерни и колеса по формуле [1, c.37]
 (2.14)
(2.14)
Подставляя число зубьев шестерни в (2.14), вычисляем делительный диаметр шестерни
 мм
мм
Подставляя число зубьев колеса в (2.14), вычисляем делительный диаметр колеса
 мм
мм
Зная делительный диаметр, можно найти диаметр вершин по формуле
 ,
(2.15)
,
(2.15)
где
 –
диаметр вершины, мм.
–
диаметр вершины, мм.
Подставляя численные значения в формулу (2.15), вычисляем диаметр вершин шестерни
 мм
мм
Подставляя численные значения в формулу (2.15), вычисляем диаметр вершин колеса
 мм
мм
Зная делительный диаметр, можем найти диаметр впадин по формуле
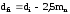 (2.16)
(2.16)
Подставляя численные значения в формулу (2.16), вычисляем диаметр впадин шестерни
 мм
мм
Подставляя численные значения в формулу (2.16), вычисляем диаметр впадин колеса
 мм
мм
Определим ширину зубьев шестерни по формуле
 мм,
(2.17)
мм,
(2.17)
где
 – ширина зубьев шестерни, мм.
– ширина зубьев шестерни, мм.
Из конструктивных соображений ширину зубьев колеса можно вычислить по формуле
 мм,
(2.18)
мм,
(2.18)
где
 –
ширина зубьев колеса, мм.
–
ширина зубьев колеса, мм.
Результаты всех вычислений сведены в табл. 2.1.
Таблица 2.1
Результаты проектировочного расчета
|
|
|
|
|
z |
d,мм |
da,мм |
df,мм |
|
|
Шестерня |
140 |
2,5 |
|
19 |
49,259 |
54,259 |
43,009 |
49 |
|
Колесо |
89 |
230,742 |
235,742 |
224,492 |
46 |
2.2. Проверочный расчет зубьев на контактную выносливость
Задачей данного раздела является проверка зубьев на контактную выносливость. Видом разрушения является усталостная поломка.
Критерий расчета – контактная выносливость.
 ,
(2.19)
,
(2.19)
где
 – фактическое контактное напряжение,
Н/мм2;
– фактическое контактное напряжение,
Н/мм2;
 – нормативное контактное напряжение,
Н/мм2.
– нормативное контактное напряжение,
Н/мм2.
В соответствии с [1, c.38] фактическое напряжение можно вычислить по формуле
 ,
(2.20)
,
(2.20)
где
 – коэффициент, учитывающий форму
сопряженных поверхностей зубьев в
полюсе зацепления;
– коэффициент, учитывающий форму
сопряженных поверхностей зубьев в
полюсе зацепления;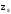 – коэффициент, учитывающий суммарную
длину контактных линий;
– коэффициент, учитывающий суммарную
длину контактных линий; – ширина колеса, мм.
– ширина колеса, мм.
 вычисляют
по формуле [1, с.32]
вычисляют
по формуле [1, с.32]
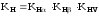 ,
(2.21)
,
(2.21)
где
 –
коэффициент, учитывающий неравномерное
распределение нагрузки между зубьями.
–
коэффициент, учитывающий неравномерное
распределение нагрузки между зубьями.
Линейная скорость шестерни определяется по формуле
 м/с,
(2.22)
м/с,
(2.22)
где V1 – линейная скорость шестерни, м/с.
Так как линейная
скорость шестерни меньше 15 м/с и передача
является быстроходной (выбираем степень
точности 7), то в соответствии с [1, с.40]
 .
.
Так как передача
является быстроходной (степень точности
7), по рекомендациям [1, с.29] выбираем
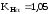 .
.
Для определения
 следует воспользоваться таблицей из
[1, с.39]. Выбираем
следует воспользоваться таблицей из
[1, с.39]. Выбираем .
.
Подставляя численные
значения коэффициентов в формулу (2.21),
вычислим значение


В соответствии с
рекомендациями [1, с.31] коэффициенты
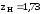 ;
; ;
;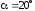 .
.
Подставляя численные значения в формулу (2.20), получим величину фактического контактного напряжения
 Н/мм2
Н/мм2
Сравним фактическое и допускаемое контактные напряжения
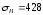 Н/мм2
<
Н/мм2
< Н/мм2
Н/мм2
Фактическое напряжение меньше допускаемого, следовательно, оставляем ранее выбранные в пункте 2.1. размеры.
2.3. Проверочный расчет зубьев на изгибную прочность
Задачей данного раздела является проверка зубьев на изгибную выносливость. Видом разрушения является усталостная поломка зуба. Критерием расчёта – изгибная выносливость.
 ,
(2.23)
,
(2.23)
где
 –
фактическое напряжение изгиба, Н/мм2;
–
фактическое напряжение изгиба, Н/мм2;
 – допускаемое напряжение изгиба, Н/мм2.
– допускаемое напряжение изгиба, Н/мм2.
Определим, где первым сломается зуб, на шестерне или на колесе. Для этого найдём допускаемое напряжение изгиба на шестерне и на колесе
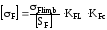 ,
(2.24)
,
(2.24)
где
 – коэффициент безопасности по изгибу;
– коэффициент безопасности по изгибу;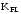 –
коэффициент долговечности;
–
коэффициент долговечности;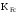 – коэффициент, учитывающий влияние
двустороннего приложения нагрузки.
– коэффициент, учитывающий влияние
двустороннего приложения нагрузки.
Учитывая, что
твердость шестерни
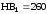 ,
следовательно по [1, с.45] выбираем
,
следовательно по [1, с.45] выбираем Н/мм2.
Твердость колеса
Н/мм2.
Твердость колеса
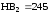 ,
тогда
,
тогда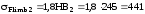 Н/мм2.
Так как приложение нагрузки одностороннее,
выбираем
Н/мм2.
Так как приложение нагрузки одностороннее,
выбираем
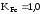 [1, с.45].
[1, с.45].
В соответствии с
рекомендациями [1, с.45] коэффициент
безопасности по изгибу
 .
.
Для всех сталей
ГОСТ принимает базовое число циклов
 [1,
с.45]. Фактическое число циклов
[1,
с.45]. Фактическое число циклов определяется из соотношения
определяется из соотношения
 (2.25)
(2.25)
Сравним
 и
и .
Так как
.
Так как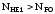 ,
следовательно, в соответствии с [1, с.45]
,
следовательно, в соответствии с [1, с.45] .
Сравним
.
Сравним и
и .
Так как
.
Так как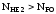 ,
следовательно, в соответствии с [1, с.45]
,
следовательно, в соответствии с [1, с.45] .
.
Найдем численное значение допускаемого контактного напряжения на шестерне, подставляя значения в формулу (2.24)
 Н/мм2
Н/мм2
Найдем численное значение допускаемого контактного напряжения на колесе, подставляя значения в формулу (2.24)
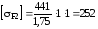 Н/мм2
Н/мм2
Теперь определим, где первым сломается зуб (на шестерне или на колесе), для этого сравним следующие соотношения [1, c.42]
 и
и
 ,
(2.26)
,
(2.26)
где
 – коэффициент, учитывающий форму зуба
шестерни;
– коэффициент, учитывающий форму зуба
шестерни; – коэффициент, учитывающий форму зуба
колеса.
– коэффициент, учитывающий форму зуба
колеса.
Коэффициент, учитывающий форму зуба, высчитывается по [1, c.46] ГОСТу 21354-75 в зависимости от эквивалентного числа зубьев
 ,
(2.27)
,
(2.27)
где
 – эквивалентное число зубьев.
– эквивалентное число зубьев.
Вычислим эквивалентное число зубьев для шестерни

С учетом интерполяции
при
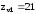 ,
,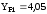 [1,
с.42]. Найдем численное значение отношения
(2.26) для шестерни
[1,
с.42]. Найдем численное значение отношения
(2.26) для шестерни
 Н/мм2
Н/мм2
Вычислим эквивалентное число зубьев для колеса
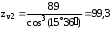
С учетом интерполяции
при
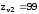 ,
, [1,
с.42]. Найдем численное значение отношения
(2.26) для колеса
[1,
с.42]. Найдем численное значение отношения
(2.26) для колеса
 Н/мм2
Н/мм2
Так как отношение
 для шестерни
меньше, чем отношение
для шестерни
меньше, чем отношение
 для колеса, то это
значит, что первым сломается зуб на
шестерне.
для колеса, то это
значит, что первым сломается зуб на
шестерне.
Сделаем проверочный расчёт для косозубой передачи шестерни
 (2.28)
(2.28)
Фактическое напряжение изгиба на шестерне можно вычислить по формуле [1, c.46]
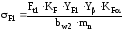 ,
(2.29)
,
(2.29)
где
 – окружная сила, Н;
– окружная сила, Н;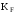 –
коэффициент нагрузки;
–
коэффициент нагрузки; – коэффициент, учитывающий угол
контактных линий;
– коэффициент, учитывающий угол
контактных линий; – коэффициент, учитывающий неравномерность
нагрузки между зубьями.
– коэффициент, учитывающий неравномерность
нагрузки между зубьями.
В соответствии с
рекомендациями [1, c.47],
принимаем коэффициент, учитывающий
неравномерность нагрузки между зубьями
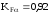 .
.
Окружная сила в соответствии с [1, c.42] вычисляется по формуле
 Н
(2.30)
Н
(2.30)
Коэффициент нагрузки в соответствии с [1, c.42] вычисляется по формуле
 ,
(2.31)
,
(2.31)
где
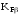 – коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба;
– коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба; – коэффициент, учитывающий динамическое
действие нагрузки.
– коэффициент, учитывающий динамическое
действие нагрузки.
Коэффициент
концентрации нагрузки и динамический
коэффициент можно вычислить по таблицам
из [1, c.43],
 ,
а для определения коэффициента
концентрации нагрузки следует вычислить
,
а для определения коэффициента
концентрации нагрузки следует вычислить
 по
формуле [1,c.33]
по
формуле [1,c.33]
 (2.32)
(2.32)
Следовательно, по
таблице [1, с.43] выбираем
 ,
тогда при симметричном расположении
зубчатых колес
,
тогда при симметричном расположении
зубчатых колес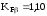 .
.
Подставляя численные значения коэффициента концентрации нагрузки и динамического коэффициента в (2.31), получим численное значение коэффициента нагрузки

Коэффициент, учитывающий угол контактных линий, определяется по формуле [1, c.46]
 (2.33)
(2.33)
Находим численное значение фактического напряжения изгиба, подставляя численные значения окружной силы, коэффициента нагрузки, коэффициента, учитывающего угол линий и коэффициента, учитывающего неравномерность распределения нагрузки между зубьями в формулу (2.29)
 Н/мм2
Н/мм2
Сравним фактическое и допускаемое напряжения изгиба зубьев
 Н/мм2
<
Н/мм2
<
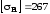 Н/мм2
Н/мм2
Так как фактическое напряжение изгиба зубьев на шестерне меньше допускаемого, следовательно, размеры передачи оставляем без изменений.

 ,мм
,мм ,мм
,мм
 ,мм
,мм