8. Проведення експериментів з обчислення похибок.
Принципові похибки чисельних методів інтегрування диференційних рівнянь мають подвійних характер:
Похибки внаслідок того, що нескінченний ряд змінюється на скінчений, який має декілька перших членів ряду; при цьому відкинуті члени утворюють похибку;
Похибки внаслідок неточного обчислення похідних у попередній точці; у власну чергу, вони зазвичай також обумовленні тим, що замість нескінченного ряду при їхньому обчисленні використовуються лише обмежена кількість його членів.
Обидві похибки - єдиного типу. Ці похибки чисельного метода не пов’язані з точністю здійснення математичних операцій,- вони викликані обмеженням нескінченних рядів скінченою кількістю їх членів. Тому вони отримали назву похибок обмежування (на відміну від похибок округлення, які визначають точність проведення обчислення)
Характерна особливість похибок обмежування - при зменшені кроку інтегрування вони також зменшувались. Цим вони суттєво відрізняються від похибок округлення, які визначаються кількістю математичних операцій. Через те, що при зменшені кроку кількість операцій, що інтегрується, пропорційно збільшується, то похибки округлення теж збільшується зі зменшенням кроку.
Якісна картина залежності похибки від кроку інтегрування наведена на Рис. 1.
Рис. 1 Залежність похибок від кроку інтегрування
Таким чином змінюючи крок інтегрування, і визначаючи похибку, з графіка похибок, маємо наступні результати:
h=0.5;
∆=
(Рис.1)
Рис.1
h=0.1;
∆=
(Рис.2)
Рис.2
h=0.05;
∆=
(Рис.3)
Рис.3
h=0.01;
∆=
(Рис.4)
Рис.4
h=0.005;
∆=
(Рис.5)
Рис.5
h=0.001;
∆
=
;
∆
=
;
(Рис.6)
Рис.6
h=0.0001;
∆
=
;
∆
=
;
(Рис.7)
Рис.7
9. Графік залежності амплітуди похибки від кроку інтегрування
Для побудови графіку використаємо окремий М-файл текст якого буде наступним:
clc
clear all
h=[0.0001,0.0003,0.0005,0.001,0.002,0.003,0.01,0.03,0.05,0.07,0.1];
dx=[1*10^(-12),3.7*10^(-12),1.85*10^(-12),5*10^(-13),7.4*10^(-13),1.33*10^(-12),1.6*10^(-10),1.35*10^(-8),1.06*10^(-7),4.15*10^(-7),1.76*10^(-6)];
loglog(h,dx,'*-');
set(gca,'FontName','MS Sans Serif')
title('Похибка чисельного інтегрування методом Рунге-Кутта 4.1');
ylabel ('Амплітуда похибки');
xlabel('Крок інтегрування');
gtext('Грандюк Андрій ПГ-11','FontName','MS Sans Serif'),grid;
В результаті маємо графік залежності амплітуди похибки від кроку інтегрування (Рис.8).
Рис.8
Знайдемо рівняння залежності похибки від кроку інтегрування:
На графіку ми бачимо лінійну залежність, отже, загальним рівнянням буде:
де 
– це
координата осі похибки;
- це
координата осі кроку інтегрування;
- це вільний член;
- це кутовий коефіцієнт, тангенс нахилу
прямої до осі кроку інтегрування.
Візьмемо дві точки з графіку похибки чисельного інтегрування:
Перша
точка має координати: 
,
;
Друга
точка має координати:
,
;
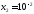Оскільки графік побудований у логарифмічному масштабі, то переведемо координати в звичайному масштабі:
; 
Кутовий коефіцієнт к знаходимо відношенням різниці координат по осі похибки до різниці координат по осі Крок інтегрування:
;
Знайдемо
вільний член
з рівняння , підставивши координати
будь-якої точки з даного графіка:
;
Оскільки
задано в логарифмічному масштабі, то
переведемо в звичайний:
;
Звідки:
;
Виводимо формулу залежності похибки від кроку інтегрування
