Архив2 / курсач docx51 / KURSACh_OLOLO

Федеральное агентство по образованию

Санкт-Петербургский государственный электротехнический

университет ˝ЛЭТИ˝

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ

по дисциплине ˝ИНФОРМАТИКА˝

Вариант № 23

Выполнил студент гр. 2402	Преподаватель
Фоминский О. Е.	Максимов А. И.

Содержание

Задание на курсовую работу	3
Задача	5
Задача 2	9
Задача 3	13
Вывод по курсовой работе	15
Список литературы	16

Задание на курсовую работу

Цель курсовой работы: уметь применять персональный компьютер и математические пакеты прикладных программ в инженерной деятельности.

Тема курсовой работы: решение математических задач с использованием математического пакета "MathCad".

Содержание курсовой работы:

1. Даны функции f(x) = √3sin(x) + cos(x) и g(x) = cos(2∙x + π/3) – 1

1. Решить уравнение f(x) = g(x).

2. Исследовать функцию h(x) = f(x) – g(x) на промежутке [0; (5∙π)/6].

2. Найти коэффициенты кубического сплайна, интерполирующего данные, представленные в векторах Vx и Vy(смотри приложение 1). Построить на одном графике: функцию f(x) и функцию f1(x), полученную после нахождения коэффициентов кубического сплайна. Представить графическое изображение результатов интерполяции исходных данных различными методами с использованием встроенных функций cspline(Vx, Vy), pspline(Vx, Vy), lspline(Vx, Vy) и interp(Vk, Vx, Vy, x).

3. Решить задачу оптимального распределения неоднородных ресурсов. На предприятии постоянно возникают задачи определения оптимального плана производства продукции при наличии конкретных ресурсов (сырья, полуфабрикатов, оборудования, финансов, рабочей силы и др.) или проблемы оптимизации распределения неоднородных ресурсов на производстве. Пусть в распоряжении завода железобетонных изделий (ЖБИ) имеется m видов сырья (песок, щебень, цемент) в объемах ai. Требуется произвести продукцию n видов. Дана технологическая норма cij потребления отдельного i-го вида сырья для изготовления единицы продукции каждого j-гo вида. Известна прибыль Пj, получаемая от выпуска единицы продукции j-гo вида. Требуется определить, какую продукцию и в каком количестве должен производить завод ЖБИ, чтобы получить максимальную прибыль.

Список обозначений и сокращений.

x – аргумент

f(x) – функция f(x)

g(x) – функция g(x)

h(x) – функция h(x)

- первая производная функции h(x)

- вторая производная функции h(x)

Vx, Vy – векторы данных

cspline, lspline, pspline – функции, используемые для нахождения коэффициентов сплайна.

f1(x) – линейная интерполяция данных, представленных в векторах Vx и Vy

Пj – прибыль предприятия

X– Количество изделий j-го наименования, которое может производить предприятие

X5, X6, X7 - фиктивные изделия, при изготовлении которых используют каждый оставшийся вид ресурса.

Задача 1.

Даны функции f(x) = √3sin(x) + cos(x) и g(x) = cos(2∙x + π/3) – 1. Решить уравнение f(x) = g(x)и исследовать функцию h(x) = f(x) – g(x) на промежутке [0; (5∙π)/6].

Решение уравнения f(x) = g(x)

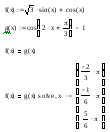
Уравнение имеет решение при x = , x= , x = .

Исследуем функцию h(x) = f(x) – g(x) на промежутке[0; (5∙π)/6].

График функции h(x) на промежутке [0; (5∙π)/6].

1. Область определения функции.

D(h(x)) =R , т.к. функция 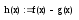определена на участке от [0; 2π], а значит и на всей числовой прямой.

2. Найдём первую производную функции и точки, в которых она равна нулю.

Она равна нулю в точках x=, x=, x=.

Из этих точек лишь x=принадлежит промежутку[0; ].

График функции h(x) и её первой производной

3. Определение монотонности функции.

Поскольку x= является точкой экстремума, характер монотонности меняется в этой точке.

значит h(x) монотонно возрастает на [0;]

значит h(x) монотонно убывает на [;].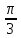

4. Нахождение экстремумов функции:

Мы уже нашли точку экстремума функции. Вычислим значение функции в этой точке.

Исследование функции на чётность:

Функция h(x)является функцией общего вида.

Нахождение областей вогнутости, выпуклости функции.

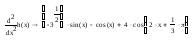
Лишь два нуля второй производной попадают в промежуток [0; ]

Задача 2.

1. Найти коэффициенты кубического сплайна, интерполирующего данные, представленные в векторах Vx и Vy.

2. Построить на одном графике: функцию f(x) и функцию f1(x), полученную после нахождения коэффициентов кубического сплайна.

3. Оценить погрешность интерполяции в точке x= 2,6. Вычислить значение функции в точке x = 1,6

4. Представить графическое изображение результатов интерполяции исходных данных различными методами с использованием встроенных функций cspline(Vx,Vy), pspline(Vx,Vy), lspline(Vx,Vy) и interp(Vk,Vx,Vy,x).

Решение задания а)

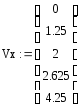
векторы данных

коэффициенты кубического сплайна

Решение задания b)

линейная интерполяция функции f

интерполяция кубическим сплайном функции f

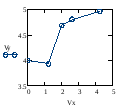
График линейной интерполяции функции f(x) и интерполяции кубическим сплайном функцииf1(x).

Решение задания c)

Погрешность интерполяции в точке x=2.6 с использованием кубического сплайна равна 0,0078, с использованием pspline равна 0,005, с использованием lspline равна 0,0051

Решение задания d)

Представление графического изображения результатов интерполяции с использованием встроенных функций pspline(Vx,Vy), interp(Vk,Vx,Vy,x). (Pic. 1)

Представление графического изображения результатов интерполяции с использованием встроенных функций lspline(Vx,Vy), interp(Vk,Vx,Vy,x). (Pic. 2)

Представление графического изображения результатов интерполяции с использованием встроенных функций cspline(Vx,Vy), interp(Vk,Vx,Vy,x). (Pic. 3)

Представление графического изображения результатов интерполяции исходных данных различными методами с использованием встроенных функций cspline(Vx,Vy), pspline(Vx,Vy), lspline(Vx,Vy) и interp(Vk,Vx,Vy,x).

Задача 3.

Решить задачу оптимального распределения неоднородных ресурсов. На предприятии постоянно возникают задачи определения оптимального плана производства продукции при наличии конкретных ресурсов (сырья, полуфабрикатов, оборудования, финансов, рабочей силы и др.) или проблемы оптимизации распределения неоднородных ресурсов на производстве. Пусть в распоряжении завода железобетонных изделий (ЖБИ) имеется m видов сырья (песок, щебень, цемент) в объемах ai. Требуется произвести продукцию n видов. Дана технологическая норма cij потребления отдельного i-го вида сырья для изготовления единицы продукции каждого j-гo вида. Известна прибыль Пj, получаемая от выпуска единицы продукции j-гo вида. Требуется определить, какую продукцию и в каком количестве должен производить завод ЖБИ, чтобы получить максимальную прибыль.

Используемые ресурсы, аi	Изготавливаемые изделия					Наличие ресурсов, аi
	И1	И2	И3	И4
Песок	8	5	8	7	20
Щебень	6	6	6	5	10
Цемент	9	6	4	9	35
Прибыль, Пj	44	54	40	30

Запишем выражение, определяющее прибыль завода.

При данных начальных условиях

,где X5, X6, X7 –фиктивные изделия.

Запишем систему уравнений, учитывающих количество используемых ресурсов и их наличие.

Функция максимизации прибыли

Так как полученное решение является десятичной дробью, то придётся использовать функцию отсечения дробной части, а не округления (если получится десятичная часть >0.5, то округление произойдёт неверно)

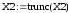
Функция отсечения дробной части

Решением является

при полученном решении максимальная прибыль равна

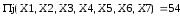
Вывод.

Согласно решению, которое выдала программа MathCAD, максимальная прибыль достигается при производстве одного изделия 2 вида и равна 54.

Однако следует заметить, что данная методика не совершенна. Если сделать устный расчёт, то можно увидеть, что произвести можно 2 изделия 4 вида и получить максимальную прибыль 60.

Общий вывод по курсовой работе.

В ходе курсовой работы были сделаны следующие задачи: во-первых, это решено уравнение f(x) = g(x), затем исследована функция h(x) = f(x)-g(x), во-вторых, найдены коэффициенты кубического сплайна, интерполирующего данные, а так же, в-третьих, решена задача оптимального распределения неоднородных ресурсов. К концу курсовой работы я научился использовать персональный компьютер и математические пакеты прикладных программ в инженерной деятельности, и решение математических задач с использованием математического пакета "MathCad".

Список литературы.

1. Ланьков А.Ю. MATHCAD 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95. / А.Ю. Ланьков. – М.: Филин, 2006. – 712 с.

2. Кудрявцев, Е.М. MathCad 2000 Pro / Е.М. Кудрявцев. – М.: Пресс, 2006. – 576 с.

3. Информатика. Базовый курс/ Симонович С.В. и др. – СПб: Издательство ″Питер″, 2005

4. Кирьянов Д.В. MathCad12. Наиболее полное руководство /Д. В. Кирьянов - СПб: БХВ-Петербург, 2005. - 566 с.

16