Архив2 / курсач docx51 / oy_kursach
.docx
Задача 1. Для электрической схемы, соответствующей номеру варианта (табл. 1.3) и изображенной на рис. 1.22 – 1.41, выполнить следующее:
1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее в двух формах: а) дифференциальной; б) символической.
2. Определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчета линейных электрических цепей.
При выполнении п.2. учесть, что одна из ЭДС в табл. 1.3 может быть задана косинусоидой (не синусоидой). Чтобы правильно записать ее в виде комплексного числа, сначала надо от косинусоиды перейти к синусоиде.
3. По результатам, полученным в п.2, определить показание ваттметра.
4. Построить топографическую диаграмму, совмещенную с векторной диаграммой токов, потенциал точки a, указанной на схеме, принять равным нулю.
|
Вариант |
16 |
|
Рисунок |
1.30 |
|
|
6 |
|
|
- |
|
|
0 |
|
|
0,8 |
|
|
- |
|
|
0,4 |
|
|
- |
|
|
100 |
|
|
- |
|
|
4000 |
|
|
|
|
|
- |
|
|
0 |
|
|
|
|
|
|
|
|
0 |
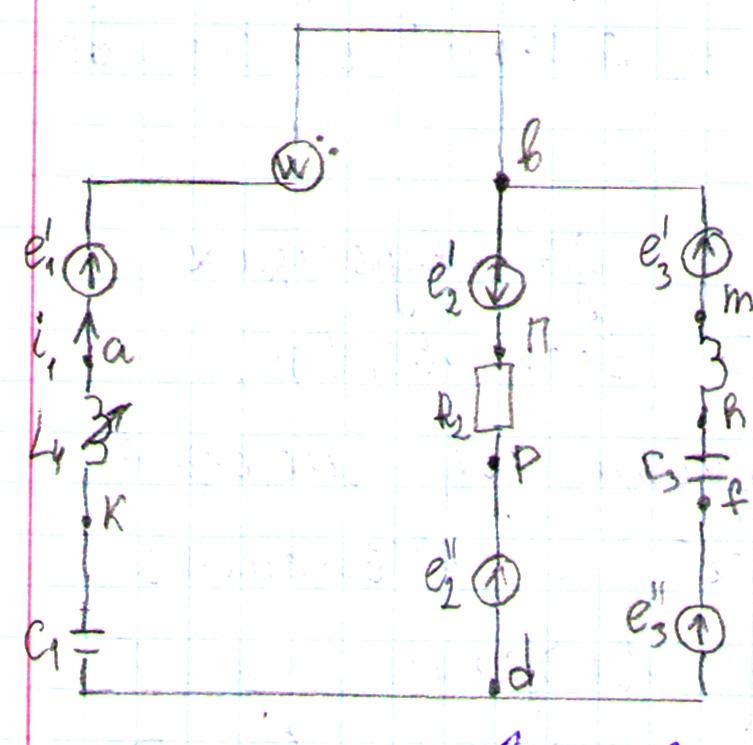
Решение

Направление контуров выбираем по часовой стрелке.
1)Система уравнений в дифференциальной форме для узла b и контуров kabdk и bmdpb:

Система уравнений в символической форме
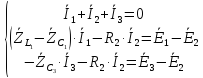
Циклическая частота равна

Записываем комплексные сопротивления:

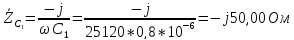

Комплексы действующих значений ЭДС:



Дополнительные 90° в показателе дает функция косинуса, так как косинус опережает синус на 90°.
2) Так как цепь содержит всего 2 узла, найдём токи методом двух узлов



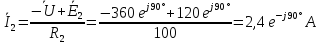
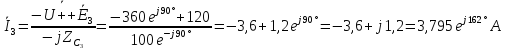
Рассчитываем
 -выделяющуюся
мощность в резисторах и
-выделяющуюся
мощность в резисторах и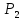 -мощность
отдаваемая для проверки баланса
мощностей.
-мощность
отдаваемая для проверки баланса
мощностей.



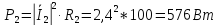


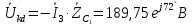

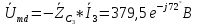
j












 a +1
a +1
p


k
Топографическая диаграмма напряжений (масштаб 1см = 10В) и векторная диаграмма токов (масштаб 1см = 1А)
Показания ваттметра определим по формуле:


Задача 2. Контур с постоянной
индуктивностью и постоянной основной
ёмкостью должен настраиваться на
заданную частоту
 (длину
волны
(длину
волны
 при помощи подстроечного переменного
конденсатора
при помощи подстроечного переменного
конденсатора
 ,
который может включаться последовательно
и параллельно с основным конденсатором
С. По приведённым в таблице данным
вычислить значения
,
который может включаться последовательно
и параллельно с основным конденсатором
С. По приведённым в таблице данным
вычислить значения
 и указать способ включения конденсатора
и указать способ включения конденсатора
 .
.
|
№ примера |
|
|
|
|
|
|
|
|
|
|
|
16 |
- |
- |
1000 |
- |
- |
|
200 |
700 |
|
|
Решение

Определим недостающие параметры.
Связь периода и частоты

Резонансная частота находится


где
 – скорость света в вакууме.
– скорость света в вакууме.
Из (2), (3)
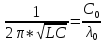 (4)
(4)
Из (4) находим

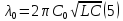
Из (5) находим C:

-
Параллельное соединение


2.Последовательное соединение
 =1,4нФ
=1,4нФ



Вывод: отрицательной ёмкости быть не
может, значит получается что конденсатор можно подключить только параллельно.
можно подключить только параллельно.
Задача 3. На рисунке 2.22 даны схемы на вход, которых воздействует одно из периодических напряжений.
-
 разложить в ряд Фурье до 5 гармоники
включительно. Построить амплитудный
и фазовый дискретный спектр
разложить в ряд Фурье до 5 гармоники
включительно. Построить амплитудный
и фазовый дискретный спектр
 .
. -
Для схемы рассчитать АЧХ и ФЧХ и построить их.
-
Рассчитать ряд Фурье для
 и построить.
и построить. -
Построить форму

|
Вариант |
16 |
|
L,мГн |
5,4 |
|
C,мкФ |
3 |
|
T,мс |
1,34 |
|
|
12,78 |
|
|
55,2 |

Рис.2.22

Рис.2.28
Решение
-
Определяем циклическую частоту


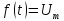

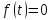
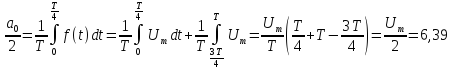








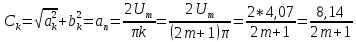

|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|










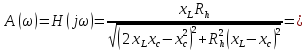




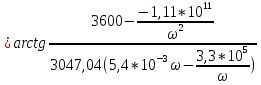

АЧХ

ФЧХ
-
Рассчитываем ряд Фурье для



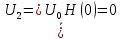

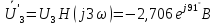

















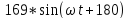








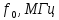



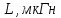

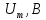
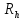 ,Ом
,Ом