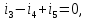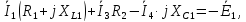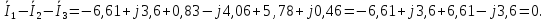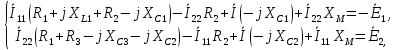Архив2 / курсач docx51 / kursach_po_TOE

Министерство образования и науки Российской Федерации

ФГОУ ВПО «Чувашский Государственный Университет им. И.Н.Ульянова»

Кафедра ТОЭ

Курсовая работа по ТОЭ:

«Расчет сложной цепи синусоидального тока»

Вариант № 47

Выполнил: ст. гр. ЭЭ-22-08

Чернышев И.В.

Проверила: Васильева В.Я.

Чебоксары 2009

Дано: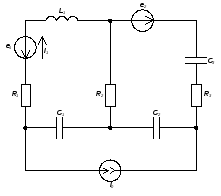

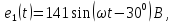
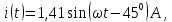
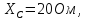
Задание №1:

1. - число узлов

- число независимых контуров (уравнений по 2-му закону Кирхгофа)

Зададимся положительными направлениями токов в ветвях и с этим условием запишем уравнения по 1-му закону Кирхгофа:

1. 

2. 

3. 

Выберем произвольно направление обхода контуров и запишем уравнения по 2-му закону Кирхгофа:

1. 

2. 

2. Составим комплексную схему замещения и запишем аналогичные уравнения для комплексных значений:

1. 

2. 

3. 

1. 

2. 

Задание №2:

В исходной схеме уберем ветвь с резистором . Зададимся положительными направлениями токов в ветвях и обходом контура. Определим токи в получившейся схеме по законам Кирхгофа:

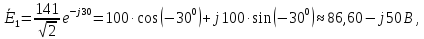
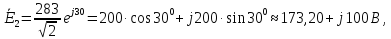
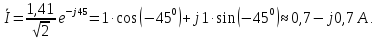
1. Составим систему уравнений по законам Кирхгофа для 1-го узла и 1-го контура:

Из второго уравнения системы:

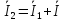
Подставим в 1-ое уравнение системы и определим ток :

Откуда получим:

Тогда ток равен:

=

Выберем направление течение контурного тока и тока источника 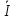и составим уравнение согласно методу контурных токов:

Зададимся положительными направлениями токов в ветвях и определим их:

=

Итак,

Задание №3:

1. Выберем направления течения контурных токов и и тока источника Запишем уравнения согласно методу контурных токов и определим токи в ветвях:

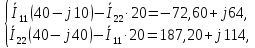
Из уравнения (1) системы:

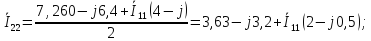
Подставляем в уравнение (2):

Откуда получим:

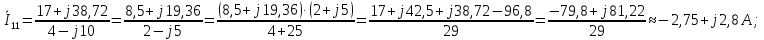
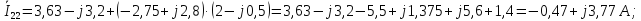
Зададимся положительными направлениями токов в ветвях и определим их:

2. Проверим баланс мощностей.

Комплексная мощность, отдаваемая источниками:

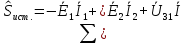
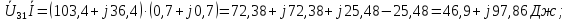
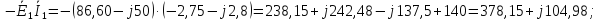
Комплексная мощность, потребляемая источниками:

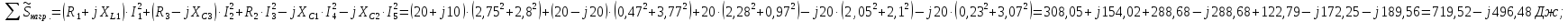
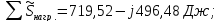
Т.к. , то расчет выполнен верно.

Задание №4:

Для исходной схемы составить систему уравнений методом узловых потенциалов и выразить токи в ветвях.

Количество узлов схемы .

Пусть . Запишем систему уравнений для остальных потенциалов:

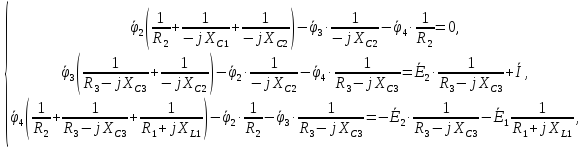
Выразим токи в ветвях согласно обобщенного закона Ома:

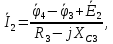
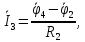
Задание №5:

В исходной схеме ветвь с сделать «особой». Полученную схему рассчитать методом узловых потенциалов. Проверить правильность вычислений по 1-му закону Кирхгофа для каждого узла.

Пусть , тогда .

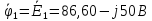Запишем уравнения согласно методу узловых потенциалов для 2-х оставшихся узлов и определим их потенциалы:

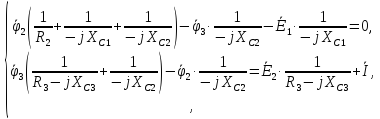
Умножим обе части уравнений системы на 10:

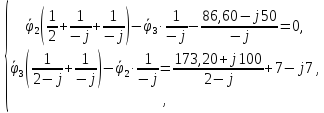
Из уравнения (1) системы:

Подставим в уравнение (2) системы и найдем :

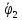Найдем токи в ветвях согласно обобщенного закона Ома:

Запишем уравнения по 1-му закону Кирхгофа:

1. 

Откуда ==

2. 

3. 

4. 

Таким образом, 1-ый закон Кирхгофа выполняется для всех узлов. Следовательно, расчет выполнен верно.

Задание №6:

В исходной схеме числить ток в ветви, указанной на схеме, методом эквивалентного генератора (значение этого тока должно совпадать с соответствующим значением тока в задании №3)

1. Разомкнем ветвь, по которой течет искомый ток, оставив ЭДС в этой ветви пунктиром (т.к. она не влияет на дальнейшее токораспределение)

Зададимся положительными направлениями токов в ветвях получившейся схемы, учитывая направление тока источника. Вычислим токи в ветвях методом контурных токов. для этого зададимся направлением течения контурного тока 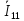и запишем соответствующее уравнение:

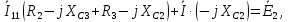
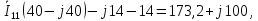
Т.к. направление и не совпадают, то

Зададимся направлением обхода контура, содержащего , и по второму закону Кирхгофа запишем уравнение для этого контура. Найдем :

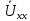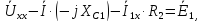
2. Найдем 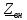цепи. Для этого составим схему, в которой все источники ЭДС закорачиваются, а ветви с источником тока убираются:

Их схемы видно, что:

Окончательно получим:

Полученное значение тока совпадает с соответствующим значением тока, найденным в задании №3, следовательно, расчет выполнен верно.

Задание №7:

В исходной схеме связать индуктивные элементы цепи взаимной индукцией. Разметка индуктивности произвольна. Для полученной схемы составить уравнения:

1. по законам Кирхгофа;

2. методом контурных токов.

1. - число узлов

- число независимых контуров

1. 

2. 

3. 

1. 

2. 

2. 

Задание №8:

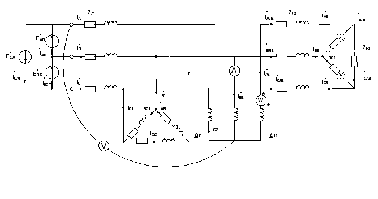
Расчет симметричных трехфазных цепей:

1. Однолинейную схему заменить развернутой схемой трехфазной цепи с учетом вида нагрузок

2. Расчитать токи генератора и всех нагрузок

3. Построить в масштабе векторную диаграмму токов

4. Определить показания приборов:

1. амперметра, включенного в фазу В нагрузки ;

2. вольтметра, включенного между зажимом А генератора и нейтральной точкой одной из нагрузок;

3. ваттметра, токовая обмотка которого включена в фазу А нагрузки , а напряжение между фазами В и С той же нагрузки;

5. Проверить баланс мощностей.

№ группы – 7, № схемы 17

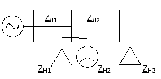
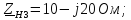
1. Схема примет вид:

Обозначим:

- линейные токи генератора;

– фазные токи генератора;

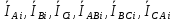- линейные и фазные токи нагрузок, где i – номер нагрузки;

- токи в линии, где i – номер линии;

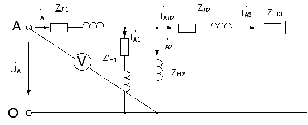
В данной схеме сразу нельзя рассчитать ни один ток. Сперва преобразуем треугольники источника и нагрузок 1 и 3 из треугольника в звезду и выделим для расчета фазу А. При этом фазное напряжение генератора, соединенного звездой в раз меньше заданного линейного (при соединении треугольником 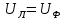) , а сопротивления:

,

Определим линейный ток (очевидно, что в линии 1 течет тот же ток - , поэтому отдельно его обозначать не будем)

Линейные токи генератора:

Фазные токи генератора:

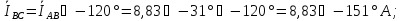
Расчитаем токи в нагрузке . Для этого по второму закону Кирхгофа опишем контур, содержащий ветвь с данной нагрузкой и фазное напряжение генератора:

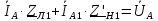
Линейные токи в нагрузке :

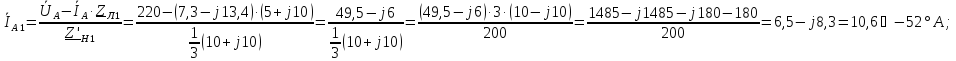
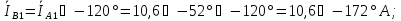
Фазные токи в нагрузке :

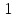Расчитаем токи в нагрузке Для этого по аналогии с предыдущими расчетами по второму закону Кирхгофа опишем контур, содержащий ветвь с данной нагрузкой и фазное напряжение генератора:

Фазные токи в нагрузке :

Токи в линии 2 определим по 1-му закону Кирхгофа для узла 1:

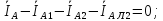
Очевидно ,что

Линейные токи нагрузки 3:

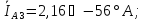
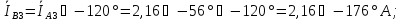
Фазные токи нагрузки 3:

3. Построим в масштабе векторную диаграмму токов.

4. Показания приборов.

1. амперметр покажет действующее значение фазного тока нагрузки 2:

2. Вольтметр покажет действующее значение суммы падений напряжений в линии 1 и нагрузке 2, т.е. фазное напряжение генератора:

3. Ваттметр покажет следующее значение:

5. Проверим баланс мощностей:

Активная мощность нагрузки:

Рективная мощность нагрузки:

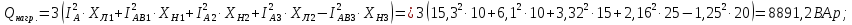
Активная мощность генератора:

Рективная мощность генератора:

Т.к. то можно утверждать, что расчет выполнен верно.