
Архив2 / курсач docx51 / Zhuravlev_A_S_3097_Kursach_TsU_i_MP
.docx|
САНКТ - ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ |
|
Курсовая работа по ЦУ и МП |
|
Журавлев Алексей, группа № 3097/1 |
|
|
|
|
|
|
|
Санкт-Петербург 2012 |
Задание:
Вариант 14
Построить шестнадцатеричный счетчик, работающий в коде Грея с индикацией на 7-сегментном индикаторе.
Введение.
Счетчик.
Счетчиком называется последовательностное устройство, имеющее несколько состояний, причем данное состояние счетчика определяется предыдущим его состоянием и значением логической переменной на входе.
Рассмотрим разные виды счетчиков:
Счетчики с последовательным переносом.
В
суммирующем счетчике с последовательным
переносом каждый входной импульс
увеличивает значение двоичного числа,
записанного в счетчик, на единицу.
Работает такой счетчик согласно
следующему правилу : 
Таблица истинности для счетчика:


Основным недостатком счетчиков с последовательным переносом является низкое быстродействие , что обусловлено последовательной работой триггеров. От этого недостатка свободны счетчики с параллельным переносом. В таких счетчиках входной сигнал может воздействовать на все триггеры счетчика одновременно, и каждый предыдущий триггер вырабатывает управляющие сигналы для всех последующих.
Поэтому будем использовать счетчик с параллельным переносом.
Счетчик с параллельным переносом.

Рисунок 2: суммирующий 3-разрядный ( m = 3 ) счетчик с параллельным переносом работающий в бинарном коде.
У бинарного кода есть один недостаток: при переключении одновременно нескольких элементов создаются токовые импульсы в электрических цепях питания схемы, которые могут вызвать сбои в работе схемы. Код Грея лишен данного недостатка, потому что при переходе от любой кодовой комбинации к следующей изменяется только один разряд.
Поэтому будем строить счетчик с параллельным переносом, работающим в коде грея.
Основная часть.
Рисунок 3: Шестнадцатеричный счетчик, с параллельным переносом работающий в коде грея:
 На
рисунке 3 введены обозначения:
На
рисунке 3 введены обозначения:
In – входной сигнал
b0,b1,b2,b3 – выходные биты шестнадцатеричного числа.
nb0,nb1,nb2,nb3 – инвертированные выходные биты.
В счетчике использованы JK- триггеры модель 7472 в программе MicroCap9.
Таблица истинности для счетчика:
|
Code Gray(out) |
|
Bin |
DEC (In) |
HEX |
|
|||||||||||
|
b3 |
b2 |
b1 |
b0 |
|
|
|
|
|
||||||||
|
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
|||||
|
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
|
|||||
|
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
2 |
2 |
|
|||||
|
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
1 |
3 |
3 |
|
|||||
|
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
4 |
4 |
|
|||||
|
0 |
1 |
1 |
1 |
|
0 |
1 |
0 |
1 |
5 |
5 |
|
|||||
|
0 |
1 |
0 |
1 |
|
0 |
1 |
1 |
0 |
6 |
6 |
|
|||||
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
7 |
7 |
|
|||||
|
1 |
1 |
0 |
0 |
|
1 |
0 |
0 |
0 |
8 |
8 |
|
|||||
|
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
9 |
9 |
|
|||||
|
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
10 |
A |
|
|||||
|
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
11 |
B |
|
|||||
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
12 |
C |
|
|||||
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
13 |
D |
|
|||||
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
14 |
E |
|
|||||
|
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
15 |
F |
|
|||||
Переходные
характеристики счетчика: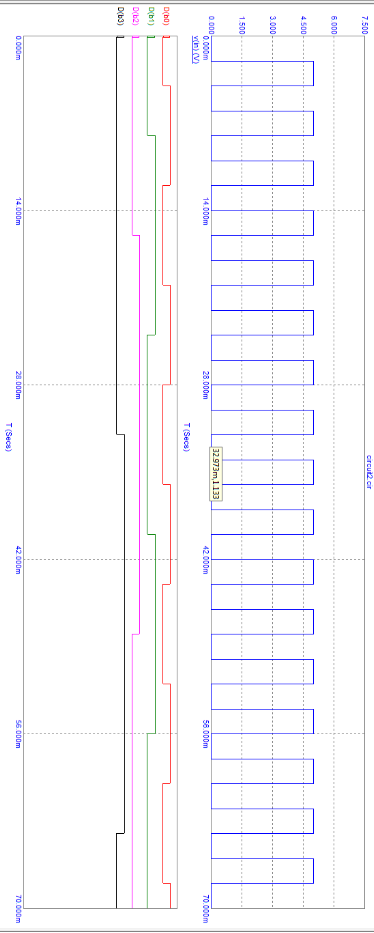
Расчет преобразователя кода грея в семи сегментный код.
Для того чтобы отображать результат счетчика на семи сегментном индикаторе нам необходимо создать преобразователь кода грея получаемого на выходе счетчика в семи сегментный код.
Составим таблицу истинности для преобразователя:
|
b3 |
b2 |
b1 |
b0 |
|
A |
B |
C |
D |
E |
F |
G |
DEC |
HEX |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
2 |
2 |
|
0 |
0 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
3 |
3 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
4 |
4 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
5 |
5 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
6 |
6 |
|
0 |
1 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
7 |
7 |
|
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
8 |
8 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
9 |
9 |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
10 |
A |
|
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
11 |
B |
|
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
0 |
12 |
C |
|
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
13 |
D |
|
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
14 |
E |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
15 |
F |

Рис. Семи сегментный индикатор.
Рассчитаем каждую функцию(A,B,C,D,E,F,G) с помощью карт Карно.

Составим и смоделируем функции по карте Карно:
Для удобства обозначим: ˥b0=nb0 ; ˥b1=nb1 ; ˥b2=nb2 ; ˥b3=nb3
1) A=(b3+b2+b1+nb0)(nb3+b2+nb1+nb0)(nb2+nb1+b0)

2) B=(nb3+b2+b1)(b3+nb2+nb0)(nb3+nb1+b0)

3)C=(nb3+b2+b1)(b3+b2+nb1+nb0)(b3+b2+b0)

4)D=(b3+nb2+b0)(b3+b2+b1+nb0)(nb3+nb2+nb1+nb0)(nb3+b2+b1+b0)

5)E=(b3+b2+b1+nb0)(nb3+nb2+b1+nb0)(b3+nb2+b0)(b3+nb2+nb1)(b3+nb1+b0)

6)F=(b3+nb2+b1+b0)(b3+b2+nb0)(b3+b2+nb1)(b2+nb1+nb0)

7)G=(nb3+b2+nb1+b0)(b3+b2+b1)(b3+b1+b0)

Переходные характеристики полученного устройства:

Список использованной литературы:
1)В.Д. Бунтов , С.Б. Макаров «Микропроцессорные системы. Часть I. Цифровые устройства»
2)Угрюмов Е. П. «Цифровая схемотехника»
3)М.А. Амелина С.А. Амелин «Программа схемотехнического моделирования Micro-Cap8»
