2.2 Первая основная квадратичная форма поверхности.

_{В произвольной точке Р поверхности (u,v) зададим направление, выбрав u=u(t), v=v(t). Отношение дифференциалов}

_{определяет направление на поверхности , имеем}

.

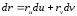_{Производная от (u,v) по направлению du: dv имеет вид:}

.

_{Малое смещение} ds по кривой _{(u(t),v(t)) на поверхности вычисляется на основании равенств .}

_{Отсюда получаем ,вычисляя скалярный квадрат}

_=,

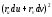_ds2=.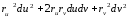

_{Введем обозначения}

_{, .}

_{Значения этих скалярных произведений зависят от выбора точки Р поверхности . Выражение:}

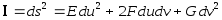
_{называется первой квадратичной формой поверхности (u,v).}

Вычисление первой квадратичной формы в произвольной и выбранной точке.

Вычислим первую квадратичную форму в выбранной точке.

Найдем

Теперь, когда найдены значения E,F и G, напишем формулу первой квадратичной формы в произвольной точке:

Нами получена формула первой квадратичной формы в произвольной точке.

Теперь, подставив наши значения в формулу первой квадратичной формы, найдем ее значение в выбранной точке:

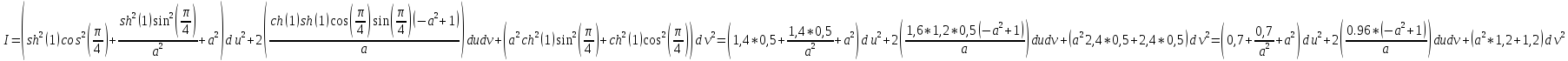
Первая квадратичная форма в выбранной точке найдена.

2.3Вторая квадратичная форма поверхности.

На поверхности (u,v) рассмотрим линию u=u(s), v=v(s) в естественной параметризации : .

Кривизна кривой : (s) =,

где k₁ кривизна кривой, - единичный вектор главной нормали кривой. Обозначим- единичный вектор нормали поверхности

(u,v) , это вектор .

Умножим скалярно и:

,

если - угол междуи. Величина

Называется нормальной кривизной (s) на поверхности (u,v) или нормальной кривизной поверхности

.

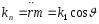Вычислим k_n в окрестности точки Р=(x₀,y₀,z₀) . Находим

,

,

,

здесь и, так как. Обозначим

, ,.

На основании формул:

и имеем

Коэффициенты L,M,N вычислены в точке Р поверхности .Выражение для нормальной кривизны линии на поверхности таково:

.

Отсюда получаем

.

Воспользуемся значением ds² из первой квадратичной формы поверхности

.

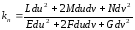Квадратичная форма

Называется второй квадратичной формой поверхности.

Вычисление второй квадратичной формы поверхности в произвольной и выбранной точке.

Найдем вторую квадратичную форму в произвольной точке:

Вычислим, для начала чему равен , подставив ранее полученные значенияE, G и F для первой квадратичной формы:

Найдем векторное произведение и:

=

Затем вычислим ,и:

Найдем коэффициенты второй квадратичной формы, подставив в формулы

наши значения:

L=

M=

N=0

Теперь напишем формулу второй квадратичной формы поверхности в произвольной точке

Вторая квадратичная форма в произвольной точке найдена.

Подставив значения в нашу формулу, получим уравнение второй квадратичной формы в выбранной точке:

Уравнение второй квадратичной формы в выбранной точке найдено.

2.4 Полная и средняя кривизны поверхности.

Рассмотрим регулярную (u,v) в окрестности точки Р.

.

Отсюда получаем

.

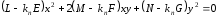Дифференцируем это неравенство по x и по y

.

Главные направления в касательной плоскости определяются этой системой уравнений, если она имеет ненулевые решения, т.е. в случае ∆=0

Значение определителя

.

Главные кривизны есть корни выписанного уравнения. Воспользуемся теоремой Виета

,

где К- полная кривизна поверхности (Гауссова кривизна),

Н- средняя кривизна поверхности.

Вычисление полной и средней кривизны поверхности

Мы вычислили полную и среднюю кривизну поверхности.