
- •1. Кривые Евклидова пространства.
- •2.Поверхности Евклидова пространства.
- •1.Кривые Евклидова пространства
- •1.1 Касательная прямая и нормальная плоскость прямой в произвольной и в выбранной точке.
- •1.2 Соприкасающаяся плоскость в произвольной и выбранной точке.
- •1.3 Кривизна и кручение кривой. Вычислительные формулы для кривизны и кручения.
- •1.4 Построение кривой
- •2.Поверхности евклидова пространства.
- •2.1 Касательная плоскость и нормаль поверхности.
- •2.2 Первая основная квадратичная форма поверхности.
- •2.3Вторая квадратичная форма поверхности.
- •2.4 Полная и средняя кривизны поверхности.
- •2.5 Изображение поверхности
- •3.Список использованной литературы.
1.2 Соприкасающаяся плоскость в произвольной и выбранной точке.
Рассмотрим
плоскости, проходящие через касательную
кривой
 (t)
в точке Р=Р (t0)
кривой. При изменении параметра t
получаем вектор
(t)
в точке Р=Р (t0)
кривой. При изменении параметра t
получаем вектор
 .
Для вектора
.
Для вектора имеет
место формула Тейлора:
имеет
место формула Тейлора:
 =
= +
+
 +
+
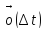 ,
,
 0.
0.
Точка
М(t0+∆t)
кривой и касательная
 P,
P,
 ꞌ(t0)
ꞌ(t0) определяют плоскость
определяют плоскость
 =
= P,
P,
 ꞌ(t0),
ꞌ(t0),
 ꞌ(t0+∆t)
ꞌ(t0+∆t) .
.
Нормальный
вектор плоскости есть
 ꞌ(t0)
ꞌ(t0)
 ꞌ(t0+∆t).
ꞌ(t0+∆t).
Плоскость
 P
,
P
,
 ꞌ(t0),
ꞌ(t0),
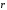 ꞌꞌ(t0)
ꞌꞌ(t0)
 называетсясоприкасающейся
плоскостью
кривой в точке t0
.
называетсясоприкасающейся
плоскостью
кривой в точке t0
.
Уравнение соприкасающейся плоскости:

Практическая часть нахождения соприкасающейся плоскости в произвольной и в выбранной точке
Найдем формулу соприкасающейся плоскости в произвольной и выбранной точке:


 =
=
 =0.
=0.
Мы
нашли формулу соприкасающейся плоскости
в произвольной точке. Теперь найдем в
произвольной точке, которую мы ранее
приняли равной
 :
:

 =
=
 =0.
=0.
Соприкасающаяся плоскость в выбранной точке найдена.
1.3 Кривизна и кручение кривой. Вычислительные формулы для кривизны и кручения.
Величина k1 называется кривизной или первой кривизной кривой r(s) в точке Р; функция k1 = k1(s) называется функцией кривизны кривой r(s), k1 ≥ 0,
 (s)
–вектор кривизны кривой
(s)
–вектор кривизны кривой
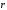 (s).
(s).
Величина
k2
называется кручением
кривой
 ꞌ(s)
или второй
кривизной кривой
ꞌ(s)
или второй
кривизной кривой
 (s)
в точке Р. При движении точки Р по кривой
(s)
в точке Р. При движении точки Р по кривой
 (s),
т.е. с изменением параметра s,
имеем функцию k2=
k2(s)
–
функцию кручения.
Знак величины k2
может
быть и положительным, и отрицательным
(s),
т.е. с изменением параметра s,
имеем функцию k2=
k2(s)
–
функцию кручения.
Знак величины k2
может
быть и положительным, и отрицательным
k1= (1);
(1);
k2
=

 (2).
(2).
Практическая часть вычисления кривизны и кручения в произвольной и выбранной точке
Вычислим, имея компоненты нашей кривой: кривизну и кручение в произвольной и выбранной точке.
Кривизна
кривой ( )
в произвольной точке вычисляется
согласно формуле (1).Подставляем наши
координаты в эту формулу, получаем:
)
в произвольной точке вычисляется
согласно формуле (1).Подставляем наши
координаты в эту формулу, получаем:


Мы
нашли кривизну кривой в произвольной
точке. Найдем кривизну выбранной точке,
подставив вместо
 значение равное 1, которое мы выбрали
ранее.
значение равное 1, которое мы выбрали
ранее.

Кривизна кривой в выбранной точке найдена.
Кручение
кривой ( )
в произвольной точке вычисляется
согласно формуле (2).Подставляем наши
координаты в эту формулу, получаем:
)
в произвольной точке вычисляется
согласно формуле (2).Подставляем наши
координаты в эту формулу, получаем:


Мы
нашли кручение кривой в произвольной
точке. Найдем кручение выбранной точке,
подставив вместо
 значение равное 1, которое мы выбрали
ранее.
значение равное 1, которое мы выбрали
ранее.

Кручение кривой в выбранной точке найдена.
1.4 Построение кривой
Изобразим нашу кривую; она будет иметь следующий вид:

2.Поверхности евклидова пространства.
Нам
даны компоненты поверхности: x= ,y=
,y=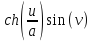 ,z=
,z= Найдем на ее примере уравнение касательной
плоскости и нормали, первую и вторую
квадратичные формы в произвольной и
выбранной точке. Вычислим полную и
среднюю кривизны поверхности. Изобразим
поверхность.
Найдем на ее примере уравнение касательной
плоскости и нормали, первую и вторую
квадратичные формы в произвольной и
выбранной точке. Вычислим полную и
среднюю кривизны поверхности. Изобразим
поверхность.
2.1 Касательная плоскость и нормаль поверхности.
Пусть
P
– точка регулярной поверхности
 (u,v).
В этой точке имеем неколлинеарные
векторы
(u,v).
В этой точке имеем неколлинеарные
векторы
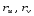 .
Для любой линии
.
Для любой линии (t)
=
(t)
=
 (u(t),v(t))
выполняется
(u(t),v(t))
выполняется
 .
.
Касательная
прямая
 P
,
P
,
 ꞌ(t)
ꞌ(t) всякой кривой
всякой кривой (t)
=
(t)
=
 (u(t),v(t))
поверхности
(u(t),v(t))
поверхности
 (u,v)
лежит в плоскости
(u,v)
лежит в плоскости
 .
Касательные всех линий поверхности
.
Касательные всех линий поверхности (u,v)
,проходящих через точку Р, образуют
плоскость.
(u,v)
,проходящих через точку Р, образуют
плоскость.
Пусть
Р=(x0,y0,z0)
и производные
 вычислены
в точке Р.
вычислены
в точке Р.
Тогда уравнение касательной плоскости таково
 .
.
Прямая
 называется нормалью поверхности
называется нормалью поверхности (u,v)
в точке Р. Ее уравнение
(u,v)
в точке Р. Ее уравнение

Нахождение касательной плоскости и нормали в произвольной и выбранной точке.
Вычислим производные по u и v. Получим следующее:






Возьмем
точки
 =
= ,
, =
= .
.
Найдем касательную плоскость в произвольной точке:

Уравнение касательной плоскости в произвольной точке найдено.
Найдем
в выбранной точке, подставив значения
 и расписавsh
и расписавsh и ch
и ch :
:


Мы нашли уравнение касательной плоскости в выбранной точке.
Теперь найдем уравнение нормали в произвольной и выбранной точке, используя теоретическую часть нашего вопроса, получим:

Получено уравнение нормали в произвольной точке. Найдем в выбранной:


Уравнение нормали в выбранной точке найдено.
