Содержание.

• 1. Кривые Евклидова пространства.

1.1 Касательная прямая и нормальная плоскость кривой.........................2 стр.

Практическая часть нахождения касательной прямой и нормальной плоскости кривой............................................................................................3 стр.

1.2Соприкасающаяся плоскость в произвольной и в выбранной точке..4 стр.

Практическая часть нахождения соприкасающейся плоскости в произвольной и в выбранной точке..............................................................5 стр.

1.3 Кривизна и кручение в выбранной и произвольной точке.....................6 стр.

Практическая часть вычисления кривизны и кручения в произвольной и выбранной точке.............................................................................................7 стр.

1.4 Построение кривой...................................................................................9 стр.

• 2.Поверхности Евклидова пространства.

2.1 Касательная плоскость и нормаль поверхности................................10 стр.

Нахождение касательной плоскости и нормали в произвольной и выбранной точке.............................................................................................................11 стр.

2.2 Первая квадратичная форма в выбранной и произвольной точке...14 стр.

Вычисление первой квадратичной формы в произвольной и выбранной точке..............................................................................................................15 стр.

2.3 Вторая квадратичная форма в выбранной и произвольной точке...17 стр.

Вычисление второй квадратичной формы поверхности в произвольной и выбранной точке...........................................................................................19 стр.

2.4 Полная и средняя кривизна поверхности.............................................22 стр.

Вычисление полной и средней кривизны поверхности...............................23 стр.

2.5 Изображение поверхности....................................................................24 стр.

3.Список использованной литературы......................................................25 стр.

1.Кривые Евклидова пространства

Нам даны параметрические координаты кривой: x= , y=,z=-. Найдем на ее примере касательную прямую, нормальную плоскость, кривизну и кручение в произвольной и выбранной точке. Построим кривую.

1.1 Касательная прямая и нормальная плоскость прямой в произвольной и в выбранной точке.

Вектор () является вектором касательной кривойв точке. Обозначим точку кривой, соответствующую значению параметра, черезP, т.е. P=P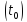. Плоскость, проходящая через точку P кривой и перпендикулярная вектору , называется нормальной плоскостью кривой в точке. По вектору=и точкеP запишем уравнения касательной прямой и нормальной плоскости кривой

+=0.

Практическая часть нахождения касательной прямой и нормальной плоскости кривой

Применим все вышесказанное к нашей кривой: найдем касательную прямую и нормальную плоскость в произвольной и выбранной точке.

В уравнение касательной прямой:

подставим наши координаты: x, y и z вместо ,исоответственно, и производныевместо, получим:

Мы получили уравнение касательной прямой в общем виде, теперь найдем уравнение прямой в выбранной точке, приняв :

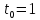Нами получено уравнение касательной прямой в выбранной точке. Теперь найдем уравнение нормальной плоскости кривой, по аналогии с нахождением уравнения касательной прямой, подставив в формулу:

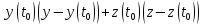+=0

наши координаты:

+=0.

Уравнение нормальной плоскости кривой в произвольной точке найдено. Напишем уравнение в выбранной точке, напомню, что . В итоге получаем:

+=0.

Нами получено уравнение нормальной плоскости кривой в выбранной точке.