Задание № 2
По данным таблицы 1 определите средний выпуск продукции (простое среднее арифметическое). Также для выпуска продукции найдите моду, медиану, дисперсию, среднее квадратическое и коэффициент вариации. Сделайте вывод.
Решение:
А) Определим средние потери рабочего времени (простое среднее арифметическое) по формуле:
Где
-
простое среднее арифметическое;
-
сумма всех значений признаков совокупности;
n- Количество признаков совокупности.
Б) Определим моду для потерь рабочего времени по формуле
Где
мода,
-
нижняя граница модального интервала,
-
величина модального интервала,
-
частота модального интервала,
-частота
интервала, предшествующего модальному,
-
частота интервала, следующего за
модальным. 
В) Определим медиану для потерь рабочего времени по формуле
Где
-
медиана,
-
нижняя граница медианного интервала,
-
величина медианного интервала,
-
сумма частот ряда,
-
частота медианного интервала,
-
сумма накопленных частот ряда,
предшествующих медианному интервалу.
Построим таблицу:
Таблица 4
|
№ группы |
Результат предприятий по потерям рабочего времени |
Потери рабочего времени |
Сумма накопленных частот |
|
1 |
43 – 54,6 |
61,5 |
61,5 |
|
2 |
54,6 – 66,2 |
239,9 |
301,4 |
|
3 |
66,2 – 77,8 |
598,2 |
899,6 |
|
4 |
77,8 – 89,4 |
446,6 |
1346,2 |
|
5 |
89,4 – 101 |
399,2 |
1745,4 |
Г) Определить дисперсию для потери рабочего времени
,
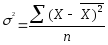где
-
сумма квадратов разности эмпирических
и средних значений выпуска продукции;
-
количество признаков совокупности.
83,72+97+1166,2+447,3+11,9+220,5+1612+366,7+23,5+477,4+1072,6+1306,8+329,4+4,6+477,4+748+223,5+4,2+394+2,1+0,7+157,5+10,7+359+2,1+23,5+1328,6+22,6+1836,2+78,3=
12888,02/30= 429,6
Д) Определим среднее квадратическое для потерь рабочего времени по формуле:
где
-
среднее квадратическое отклонение,
-
дисперсия факторного признака.
Е) Определим коэффициент вариации для потерь рабочего времени по формуле:
,
где
-
коэффициент вариации,
-
среднее квадратическое отклонение,
-
среднее значение факторного признака.
Вывод:
Средними потерями рабочего времени , для всех представленных в таблице №1 потерь рабочего времени является 57,85 ; наиболее часто встречающимся значением признака ( мода) примерно 65,3 ; вариант показателя , расположенный в середине упорядоченного ряда , делящий его на две части ( медиана) равна 64,1; среднее арифметическое квадратов отклонений отдельных значений признака от их средней арифметической равно 21, каждое значение признака отклоняется от среднего примерно 36%. Так как коэффициент вариации больше 30 , то рассмотренная совокупность неоднородна и средняя для неё типична.
Задание № 3
Имеются данные о количестве постояльцев в гостинице за три года:
Таблица 5
|
Месяц |
1998 г. |
1999 г. |
2000 г. |
|
январь |
49 |
51 |
55 |
|
февраль |
60 |
65 |
69 |
|
март |
65 |
69 |
78 |
|
апрель |
92 |
101 |
118 |
|
май |
142 |
187 |
200 |
|
июнь |
210 |
259 |
262 |
|
июль |
268 |
340 |
345 |
|
август |
310 |
335 |
340 |
|
сентябрь |
289 |
328 |
336 |
|
октябрь |
179 |
202 |
243 |
|
ноябрь |
102 |
123 |
126 |
|
декабрь |
40 |
42 |
50 |
По данным табл. 2 определить индексы сезонности:
Методом постоянной средней (простой средней арифметической);
Методом аналитического выравнивания.
Построить график сезонной волны.
Решение:
По данным табл. 5 определим индексы сезонности методом постоянной средней (простой средней арифметической).
А) Используя формулу простой средней арифметической, определим среднемесячные уровни реализации за три года:
,
где
-
среднемесячный уровень реализации,
-
сумма значений показателя совокупности
за одноименные месяцы за три года,
N - количество лет.
Январь = (49+51+55)/ 3= 52
Февраль = (60+65+69)/3= 65
Март =(65+69+78)/3=71
Апрель = (92+101+118)/3=103,6
Май = (142+187+200)/3=176,3
Июнь = (210+259+262)/3=243,7
Июль = (268+340+345)/3=317,7
Август =(310+335+340)/3=328,3
Сентябрь = (289+328+336)/3=317,7
Октябрь = (179+202+243)/3=208
Ноябрь =(102+123+126)/3=117
Декабрь = (40+42+50)/3=44
Б) Определим общую среднюю по формуле:
,
где
-
общая средняя,
-
сумма среднемесячного уровня реализации,
N - количество лет.
=
2044,3/ 12= 170,35
В) Определим индексы сезонности по формуле:
,
где
-
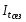индекс сезонности,
-
среднемесячный уровень реализации,
-
общая средняя.
Январь
=
Фвраль
=
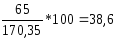
Март
=
Апрель
=
Май
=
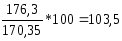
Июнь
=
Июль
=
Август
=
Сентябрь
=
Октябрь
=
Ноябрь
=
Декабрь
=
Вывод:
Индексы сезонности показывают наибольшее на июль (186,5) и август(192,7), наименьшее на декабрь (25,8) и январь (30,5).
2.По данным таблицы №5 определим индексы сезонности методом аналитического выравнивания:
Для расчёта индекса сезонности применяется формула:
,
где
-
индекс сезонности,
Эмпирические уровни ряда,
-
Теоретические уровни ряда,
N - Число лет.
А) Для этого определим теоретические значения из уравнения :
где
-Теоретические
уровни ряда,
-
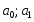Параметры прямой,
-
Показатель времени.
Для
нахождения параметров
необходимо
решить систему уравнений:
где
y- Фактические уровни ряда,
n- Число уровней.
Результаты расчётов представим в таблице:
|
Месяцы |
Уi |
t |
t*t |
y*t |
yt |
yi/уt*100% |
|
1998 | ||||||
|
январь |
49 |
-17,5 |
306,25 |
-857,5 |
130,9 |
37,4 |
|
февраль |
60 |
-16,5 |
272,25 |
-990 |
133,2 |
45,1 |
|
март |
65 |
-15,5 |
240,25 |
-1007,5 |
135,4 |
48 |
|
апрель |
92 |
-14,5 |
210,25 |
-13334 |
137,7 |
66,8 |
|
май |
142 |
-13,5 |
182,25 |
-1914 |
139,9 |
101,5 |
|
июнь |
210 |
-12,5 |
156,25 |
-2625 |
142,2 |
147,7 |
|
июль |
268 |
-11,5 |
132,25 |
-3082 |
144,4 |
185,6 |
|
август |
310 |
-10,5 |
110,25 |
-3255 |
146,7 |
211,3 |
|
сентябрь |
289 |
-9,5 |
90,25 |
-2745,5 |
148,9 |
194,1 |
|
октябрь |
179 |
-8,5 |
72,25 |
-1521,5 |
151,2 |
118,4 |
|
ноябрь |
102 |
-7,5 |
56,25 |
-765 |
153,4 |
66,5 |
|
декабрь |
40 |
-6,5 |
42,25 |
-260 |
155,7 |
25,7 |
|
1999 | ||||||
|
январь |
51 |
-5,5 |
30,25 |
-280,5 |
158,8 |
32,1 |
|
февраль |
65 |
-4,5 |
20,25 |
-292,5 |
160,2 |
40,6 |
|
март |
69 |
-3,5 |
12,25 |
-241,5 |
162,4 |
42,5 |
|
апрель |
101 |
-2,5 |
6,25 |
-252,5 |
164,8 |
61,3 |
|
май |
187 |
-1,5 |
2,25 |
-280,5 |
166,9 |
112,1 |
|
июнь |
259 |
-0,5 |
0,25 |
-129,5 |
169,2 |
153,1 |
|
июль |
340 |
0,5 |
0,25 |
170 |
171,4 |
198,4 |
|
август |
335 |
1,5 |
2,25 |
502,5 |
173,7 |
192,9 |
|
сентябрь |
328 |
2,5 |
6,25 |
820 |
175,9 |
224,8 |
|
октябрь |
202 |
3,5 |
12,25 |
707 |
178,2 |
113,4 |
|
ноябрь |
123 |
4,5 |
20,25 |
553,5 |
180,4 |
68,2 |
|
декабрь |
42 |
5,5 |
30,25 |
231 |
182,7 |
22,9 |
|
2000 | ||||||
|
январь |
55 |
6,5 |
42,25 |
357,5 |
184,9 |
25,8 |
|
февраль |
69 |
7,5 |
56,25 |
517,5 |
187,2 |
36,8 |
|
март |
78 |
8,5 |
72,25 |
663 |
189,4 |
41,2 |
|
апрель |
118 |
9,5 |
90,25 |
1121 |
191,7 |
60,8 |
|
май |
200 |
10,5 |
110,25 |
2100 |
193,9 |
103,2 |
|
июнь |
262 |
11,5 |
132,25 |
3013 |
195,2 |
134,1 |
|
июль |
345 |
12,5 |
156,25 |
4312,5 |
198,4 |
173,9 |
|
август |
340 |
13,5 |
182,25 |
4590 |
200,7 |
169,4 |
|
сентябрь |
336 |
14,5 |
210,25 |
4872 |
202,9 |
165,6 |
|
октябрь |
243 |
15,5 |
240,25 |
3766,5 |
204,2 |
119 |
|
ноябрь |
126 |
16,5 |
272,25 |
2079 |
207,4 |
60,7 |
|
декабрь |
50 |
17,5 |
306,25 |
875 |
209,7 |
23,8 |
|
Итого |
6130 |
0 |
3881 |
8754 |
|
|
Б)
Вычислим параметры
.
Так как суммаt=0,
то система уравнений примет вид:
тогда
,
,
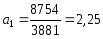
Тогда
уравнение
примет
вид:
В)
Подставив в полученное уравнение
значение t
( по месяцам) , получим следующее
теоретическое значение
ряда:
|
месяц |
yt |
|
1998 | |
|
январь |
170,3+2,25*(-17,5)=130,9 |
|
февраль |
170,3+2,25*(-16,5)=133,2 |
|
март |
170,3+2,25*(-15,5)=135,4 |
|
апрель |
170,3+2,25*(-14,5)=137,7 |
|
май |
170,3+2,25*(-13,5)=139,9 |
|
июнь |
170,3+2,25*(-12,5)=142,2 |
|
июль |
170,3+2,25*(-11,5)=144,4 |
|
август |
170,3+2,25*(-10,5)=146,7 |
|
сентябрь |
170,3+2,25*(-9,5)=148,9 |
|
октябрь |
170,3+2,25*(-8,5)=151,2 |
|
ноябрь |
170,3+2,25*(-7,5)=153,4 |
|
декабрь |
170,3+2,25*(-6,5)=155,7 |
|
1999 | |
|
январь |
170,3+2,25*(-5,5)=158,8 |
|
февраль |
170,3+2,25*(-4,5)=160,2 |
|
март |
170,3+2,25*(-3,5)=162,4 |
|
апрель |
170,3+2,25*(-2,5)=164,8 |
|
май |
170,3+2,25*(-1,5)=166,9 |
|
июнь |
170,3+2,25*(-0,5)=169,2 |
|
июль |
170,3+2,25*(0,5)=171,4 |
|
август |
170,3+2,25*(1,5)=173,7 |
|
сентябрь |
170,3+2,25*(2,5)=175,9 |
|
октябрь |
170,3+2,25*(3,5)=178,2 |
|
ноябрь |
170,3+2,25*(4,5)=180,4 |
|
декабрь |
170,3+2,25*(5,5)=182,7 |
|
2000 | |
|
январь |
170,3+2,25*(6,5)=184,9 |
|
февраль |
170,3+2,25*(7,5)=187,2 |
|
март |
170,3+2,25*(8,5)=189,4 |
|
апрель |
170,3+2,25*(9,5)=191,7 |
|
май |
170,3+2,25*(10,5)=193,9 |
|
июнь |
170,3+2,25*(11,5)=195,2 |
|
июль |
170,3+2,25*(12,5)=198,4 |
|
август |
170,3+2,25*(13,5)=200,7 |
|
сентябрь |
170,3+2,25*(14,5)=202,9 |
|
октябрь |
170,3+2,25*(15,5)=204,2 |
|
ноябрь |
170,3+2,25*(16,5)=207,4 |
|
декабрь |
170,3+2,25*(17,5)=209,7 |
Г) Для каждого месяца процента отношения эмпирических уровней ряда к теоретическим по формуле:
|
месяц |
Yt/yi*100% |
|
1998 | |
|
январь |
49/130,9*100=37,4 |
|
февраль |
60/133,2*100=45,1 |
|
март |
65/135,4*100=48 |
|
апрель |
92/137,7*100=66,8 |
|
май |
142/139,9*100=101,5 |
|
июнь |
210/142,2*100=147,7 |
|
июль |
268/144,4*100=185,6 |
|
август |
310/146,7*100=211,3 |
|
сентябрь |
289/148,9*100=194,1 |
|
октябрь |
179/151,2*100=118,4 |
|
ноябрь |
102/153,4*100=66,5 |
|
декабрь |
40/155,7*100=25,7 |
|
1999 | |
|
январь |
51/158,8*100=32,1 |
|
февраль |
65/160,2*100=40,6 |
|
март |
92/162,4*1000=42,5 |
|
апрель |
101/164,8*100=61,3 |
|
май |
187/166,9*100=112,1 |
|
июнь |
259/169,2*100=153,1 |
|
июль |
340/171,4*100=198,4 |
|
август |
335/173,7*100=192,9 |
|
сентябрь |
328/175,9*100=224,8 |
|
октябрь |
202/178,2*100=113,4 |
|
ноябрь |
123/180,4*100=68,2 |
|
декабрь |
42/182,7*100=22,9 |
|
2000 | |
|
январь |
55/184,9*100=29,8 |
|
февраль |
69/187,2*100=36,8 |
|
март |
78/189,4*100=41,2 |
|
апрель |
118/191,7*100=60,8 |
|
май |
200/193,9*100=103,2 |
|
июнь |
262/195,2*100=134,1 |
|
июль |
345/198,4*100=173,9 |
|
август |
340/200,7*100=169,4 |
|
сентябрь |
336/202,9*100=165,6 |
|
октябрь |
243/204,2*100=119,0 |
|
ноябрь |
126/207,4*100=60,7 |
|
декабрь |
50/209,7*100=23,8 |
Д) Просуммируем процентные отношения по одноимённым месяцам за 3 года, рассчитаем индексы сезонности. Все результаты представим в таблице:
Таблица 6
|
месяцы |
эмпирические уровни |
теоретические уровни |
процентные отношения |
сумма процентных отношений |
индексы сезонности | |||||||||
|
|
1998 |
1999 |
2000 |
1998 |
1999 |
2000 |
1998 |
1999 |
2000 |
| ||||
|
январь |
49 |
51 |
55 |
37,4 |
32,1 |
25,8 |
130,9 |
158,8 |
184,9 |
99,3 |
33,1 | |||
|
февраль |
60 |
65 |
69 |
45,1 |
40,6 |
36,8 |
158,8 |
184,9 |
474,7 |
122,5 |
40,8 | |||
|
март |
65 |
69 |
78 |
48 |
42,5 |
41,2 |
160,2 |
187,2 |
480,6 |
131,7 |
43,9 | |||
|
апрель |
92 |
101 |
118 |
66,8 |
61,3 |
60,8 |
162,4 |
189,4 |
1917 |
188,9 |
62,9 | |||
|
май |
142 |
187 |
200 |
101,5 |
112,1 |
103,2 |
164,8 |
191,7 |
494,2 |
316,8 |
105,6 | |||
|
июнь |
210 |
259 |
262 |
147,7 |
153,1 |
134,1 |
166,9 |
193,9 |
500,7 |
434,9 |
144,9 | |||
|
июль |
268 |
340 |
345 |
185,6 |
198,4 |
173,9 |
169,2 |
195,2 |
506,6 |
557,9 |
185,9 | |||
|
август |
310 |
335 |
340 |
211,3 |
192,9 |
169,4 |
171,4 |
198,4 |
514,2 |
573,6 |
191,2 | |||
|
сентябрь |
289 |
328 |
336 |
194,1 |
224,8 |
165,6 |
173,7 |
200,7 |
521,1 |
584,5 |
194,8 | |||
|
октябрь |
179 |
202 |
243 |
118,4 |
113,4 |
119 |
175,9 |
202,9 |
527,7 |
350,8 |
116,9 | |||
|
ноябрь |
102 |
123 |
126 |
66,5 |
68,2 |
60,7 |
178,2 |
204,2 |
533,6 |
195,4 |
65,1 | |||
|
декабрь |
40 |
42 |
50 |
25,7 |
22,9 |
23,8 |
180,4 |
207,4 |
541,2 |
72,4 |
24,1 | |||
3.Построим график сезонной волны:
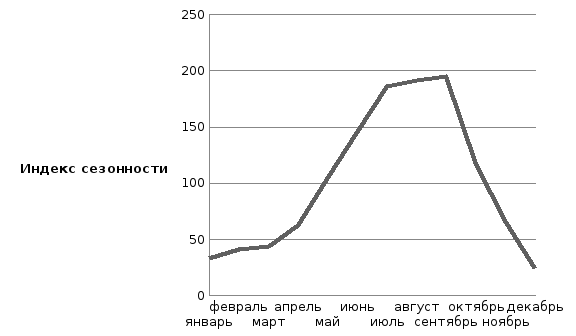
Вывод: Таким образом, график сезонной волны, полученный методом постоянной средней и аналитического выравнивания, наглядно показывают, что наибольшее количество постояльцев в гостинице бывает в августе и в сентябре, а наименьшее – в декабре и в январе.
Задание №4.