5. Контрольные карты

Впервые контрольные карты были предложены в 1924 году У.Шухартом (США) с намерением исключить необычную вариацию, отделяя вариации, которые обусловлены определёнными причинами, от тех, что обусловлены случайными причинами.[13] Первоначально они использовались для регистрации результатов измерений требуемых свойств продукции. Выход параметра за границы поля допуска свидетельствовал о необходимости остановки производства и проведении корректировки процесса в соответствии со знаниями специалиста, управляющего производством.

Контрольные карты – это инструмент, позволяющий отслеживать ход протекания процесса и воздействовать на него (с помощью соответствующей обратной связи), предупреждая его отклонения от предъявляемых к процессу требований.[6]

Контрольная карта состоит из центральной линии, двух контрольных пределов (над и под центральной линией) и значений характеристики (показателя качества), нанесенных на карту для представления состояния процесса.[8] Если все эти значения оказываются внутри контрольных пределов, не проявляя каких бы то ни было тенденций, то процесс рассматривается как находящийся в контролируемом состоянии. Если же, напротив, они попадут за контрольные пределы или примут какую-нибудь необычную форму, то процесс считается вышедшим из-под контроля. Примеры приведены на рисунке 4.1.

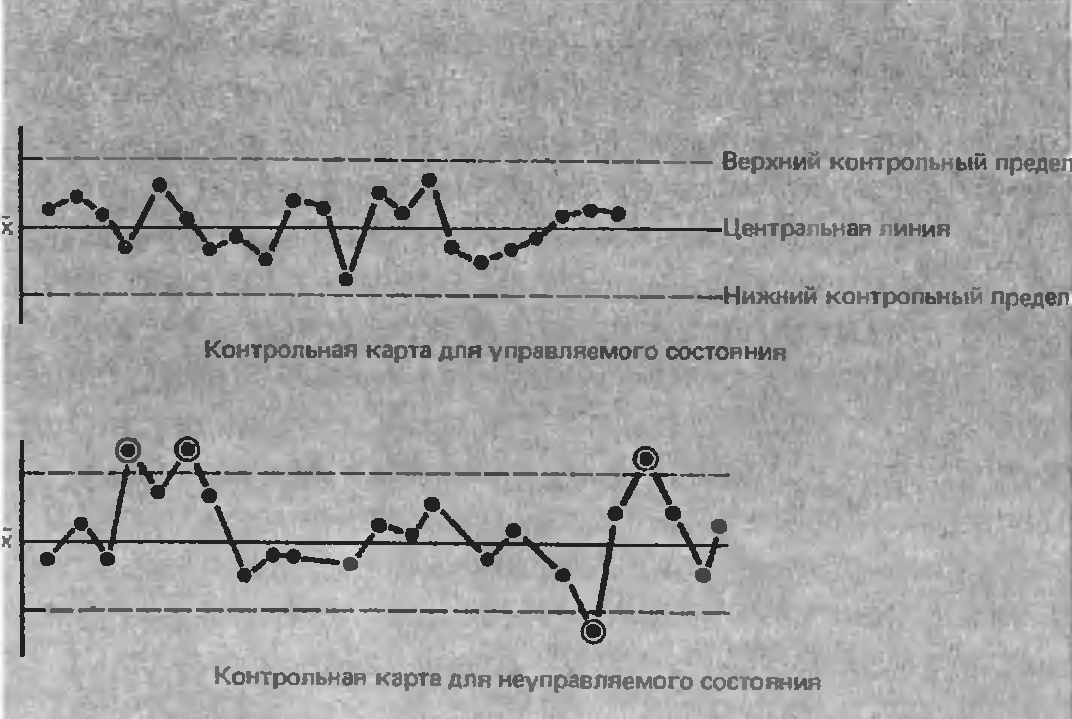
Рисунок 5.1 – Примеры контрольных карт

Находится ли процесс в контролируемом состоянии или нет, определяется по контрольной карте на основании следующих критериев.

1) Выход точки за контрольные пределы.

2) Серия – это проявление такого состояния, когда точки неизменно оказываются по одну сторону от средней линии; число таких точек называется длиной серии. Серия длиной в 7 точек рассматривается как ненормальная. Даже если длина серии оказывается менее 6, в ряде случаев ситуацию следует рассматривать как ненормальную, когда:

а) не менее 10 из 11 точек оказываются по одну сторону от центральной линии;

б) не менее 12 из 14 точек оказываются по одну сторону от центральной линии;

в) не менее 16 из 20 точек оказываются по одну сторону от центральной линии;

Рисунок 5.2 – Примеры серий

3) Тренд (дрейф). Если точки образуют непрерывно повышающуюся или понижающуюся кривую, говорят, что имеет место тренд.

Рисунок 5.3 – Примеры тренда

4) Приближение к контрольным пределам. Рассматриваются точки, которые приближаются к 3-сигмовым контрольным пределам, причём если 2 или 3 точки оказываются за 2-сигмовыми линиями, то такой случай надо рассматривать как ненормальный.

Рисунок 5.4 – Пример приближения к контрольным пределам (2 из 3 точек)

5) Приближение к центральной линии. Когда большинство точек концентрируется внутри центральных полуторасигмовых линий, делящих пополам расстояние между центральной линией и каждой из контрольных линий, это обусловлено неподходящим способом разбиения на подгруппы. Приближение к центральной линии вовсе не означает, что достигнуто контролируемое состояние, напротив, это означает, что в подгруппах смешиваются данные из различных распределений, что делает размах контрольных пределов слишком широким. В таком случае надо изменить способ разбиения на подгруппы.

Рисунок 5.5 – Пример приближения к центральной линии

6) Периодичность. Когда кривая повторяет структуру «то подъём, то спад» с примерно одинаковыми интервалами времени, это тоже ненормально.[13]

Рисунок 5.6 – Пример периодичности

Контрольная карта может указать на наличие потенциальных проблем до того, как начнется выпуск дефектной продукции [8].

Существует большое количество различных типов контрольных карт. В данной курсовой работе мы уделяем внимание контрольным картам средних – размахов (). Эта карта используется для анализа и управления процессами, показатели качества которых представляют собой непрерывные величины и несут наибольшее количество информации о процессе. Величина— есть среднее арифметическое значение для подгруппы, a R — выборочный размах для той же подгруппы. Обычно R-карту используют для контроля и управления разбросом (размахом) внутри подгруппы [12].

Для построения контрольных карт используем программу Statistica.

Рассмотрим построение контрольной карты для ТС-2010 №1-100 и №400-500, физика. Расслоение сделаем по 20 группам. Необходимо построить карты средних–размахов и найти:

1) среднее значение: , (5.1)

где - суммарное значение баллов учащихся в i-ой группе;

n –объём выборки для группы;

2) размах: , (5.2)

где - наибольшее и наименьшее значения результатов в выборке.

Далее необходимо вычислить значения, характеризующие положение каждой контрольной линии для - карты и для R-карты по следующим формулам:

а) для - карты:

- верхний контрольный предел: , (5.3)

где (m – количество групп), (5.4)

(5.5)

- нижний контрольный предел: , (5.6)

- центральная линия: ; (5.7)

б) для R-карты:

- верхний контрольный предел: UCL = D₄·; (5.8)

- нижний контрольный предел: LCL = D₃·_{; (5.9)}

- центральная линия: CL = . (5.10)

Нижний предел не рассматривается, когда n < 7. Константы А₂ , D₄ , D₃ — коэффициенты, определяемые объемом подгрупп n.

Расчётная часть.

1) Рассмотрим ТС-2010: №1-100, физика.

Таблица 5.1 - Статистика баллов учащихся №1-100

№ группы	№ выборки						Среднее значение i		Размах Ri
	x1	x2	x3	x4	x5
1	100	82	94	71	82	85,8		29
2	64	82	78	72	73	73,8		18
3	74	73	73	78	82	76		9
4	69	69	75	75	73	72,2		6
5	66	59	78	75	67	69		19
6	72	73	100	78	75	79,6		28
7	65	62	71	71	68	67,4		9
8	71	68	61	64	68	66,4		10
9	70	66	75	73	73	71,4		9
10	68	65	73	68	68	68,4		8
11	74	67	67	67	64	67,8		10
12	70	66	68	66	63	66,6		7
13	66	61	61	68	68	64,8		7
14	67	64	65	63	63	64,4		4
15	62	73	74	66	61	67,2		13
16	71	76	63	61	71	68,4		15
17	68	66	74	72	66	69,2		8
18	63	70	67	72	64	67,2		9
19	62	56	62	55	68	60,6		13
20	64	67	64	61	70	65,2		9

_μ=

При n=5, d₂=2,33.

σ=

_{Контрольные границы для} -карты:

=69,57;

_{Контрольные границы для} -карты: UCL = D₄·

LCL - не определена, т.к. нижний предел не рассматривается, когда n < 7, CL=12.

_{Рисунок 5.7 - X-R-контрольные карты}

Из анализа данной контрольной карты видно, что имеется не значительный разброс значений относительно средней линии. Три точки выходят за контрольные пределы. Это свидетельствует о том, что в 1,6 и 19 группах учащихся наблюдается разброс баллов по физике. Причиной может служить различная подготовка к экзамену учащихся. Необходимо улучшить уровень подготовки школьников. Также наблюдается серия из 9 точек, лежащих по одну сторону от средней линии. Такое состояние является ненормальным.

2) Рассмотрим ТС-2010: №400-500, физика.

Таблица 5.2 - Статистика баллов учащихся №400-500

№ группы	№ выборки						Среднее значение i		Размах Ri
	x1	x2	x3	x4	x5
1	57	63	62	61	52	59		11
2	56	56	49	46	46	50,6		10
3	60	53	54	56	55	55,6		7
4	55	45	61	56	59	55,2		16
5	54	52	55	54	49	52,8		6
6	49	70	62	60	58	59,8		21
7	56	55	53	63	62	57,8		10
8	59	54	54	45	58	54		14
9	57	57	52	49	46	52,2		11
10	65	56	50	56	54	56,2		15
11	54	48	59	54	53	53,6		11
12	52	50	48	62	57	53,8		14
13	56	58	50	53	46	52,6		12
14	55	53	52	49	58	53,4		9
15	63	56	55	53	52	55,8		11
16	54	53	52	52	53	52,8		2
17	50	40	60	57	54	52,2		20
18	54	53	48	56	55	53,2		8
19	55	53	59	56	59	56,4		6
20	52	49	49	46	54	50		8

_μ=

При n=5, d₂=2,33.

σ=

_{Контрольные границы для} -карты:

=54,35;

_{Контрольные границы для} -карты: UCL = D₄·

LCL - не определена, т.к. нижний предел не рассматривается, когда n < 7, CL=11,1.

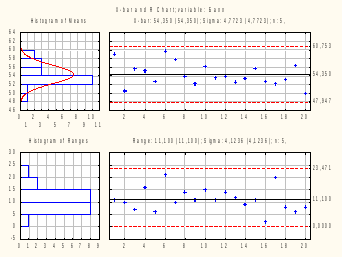
_{Рисунок 5.8 – X-R-контрольные карты}

Из анализа данной контрольной карты видно, что имеется не значительный разброс значений относительно средней линии, но они не выходят за границы. Это свидетельствует о том, что баллы учащихся примерно одинаковы, т.е. примерно одинаковый их уровень подготовки.

_{Сравнивая построенные контрольные карты можно сказать, что во втором случае (учащиеся №}400-500 ) процесс протекает намного лучше, чем в первом случае.