Добавил:

f24 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северный (Арктический) федеральный университет им. М. В. Ломоносова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Архив2 / курсовая doc25x / KURSOVAYa_Zhenya.docx

Скачиваний:

127

Добавлен:

07.08.2013

Размер:

2.32 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

5.2Устройство теодолита и тахеометра

Теодолит– геодезический инструмент для определения направлений и измерения горизонтальных и вертикальных углов при геодезических работах, топографических съемках, в строительстве и других видах работ. Теодолиты применяют для измерения горизонтальных, вертикальных углов, расстояний нитяным дальномером, магнитных азимутов с использованием буссоли и нивелирования как горизонтальным, так и наклонным лучом.

Современный теодолит (рассмотрен на примере теодолита Т30) представляет собой оптическую трубу, движущуюся по двум перпендикулярным осям, горизонтальной и вертикальной. Если оптическая труба направлена на желаемый объект, угол каждой из этих осей может быть измерен с высокой точностью, обычно по шкале, градуированной в угловых секундах. Для плавного вращения алидады и лимба имеется система осей, а сами вращения регулируются зажимными и наводящими винтами. Для установки теодолита на земле применяется специальный штатив, а совмещение центра лимба с отвесной линией, проходящей через вершину измеряемого угла, осуществляется с помощью оптического центрира или нитяного отвеса. Стороны измеряемого угла проецируются на плоскость лимба подвижной вертикальной плоскостью, которая называется коллимационной плоскостью. Коллимационная плоскость образуется визирной осью зрительной трубы при вращении трубы вокруг своей оси. Визирная ось трубы (или визирная линия) – это воображаемая линия, проходящая через центр сетки нитей и оптический центр объектива трубы.

Теодолит состоит из следующих частей (рис. 3):

1 – лимб – угломерный круг с делениями от 0° до 360°; при измерении углов лимб является рабочей мерой (на рис. не показан);

2 – алидада – подвижная часть теодолита, несущая систему отсчитывания по лимбу и визирное устройство – зрительную трубу;

3 – зрительная труба, крепится на подставках на алидадной части. Обычно всю вращающуюся часть теодолита называют алидадной частью (алидадой). При общей оси вращения лимба и алидады конструкция теодолита обеспечивает возможность как их совместного вращения, так и вращения по отдельности.

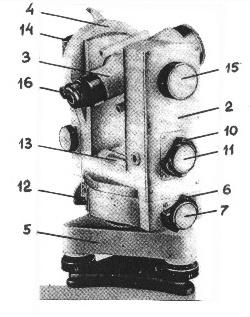
Рисунок 1. Устройство оптического теодолита

4 – вертикальный круг– служит для измерения вертикальных углов;

5 – подставка с тремя подъемными винтами;

6-11 – зажимные и наводящие винты вращающихся частей теодолита (лимба (8,9), алидады(6,7), трубы (10,11). Зажимные винты называют также закрепительными и стопорными, а наводящие – микрометренными;

12 – винт перестановки лимба;

13 – уровень при алидаде горизонтального круга;

14 – уровень вертикального круга;

15 – винт фокусировки трубы;

16 – окуляр микроскопа отсчетного устройства.

Для установки теодолита над точкой местности используется штатив с крючком для отвеса, площадкой для установки подставки теодолита и становым винтом, предназначенным для фиксации длины ножек штатива.

В комплект теодолита Т30 также входят окулярные насадки, применяемые для удобства наблюдения предметов, расположенных под углами более 45к горизонту и центрирования теодолита с помощью зрительной трубы, и ориентир-буссоль. Для определения расстояний по нитяному дальномеру и измерения углов в работе с теодолитом применяются нивелирные рейки. Теодолит, имеющий вертикальный круг, устройство для измерения расстояний (дальномер) и буссоль, называется теодолитом-тахеометром.

В настоящее время получили распространение тахеометры, позволяющие определять не только углы, но и расстояния до точек.

Тахеометр– геодезический прибор для измерения расстояний, горизонтальных и вертикальных углов. Используется для определения координат и высот точек местности при топографической съёмке местности, при разбивочных работах, выносе на местность высот и координат проектных точек. Тахеометры обеспечивают большую быстроту съемки за счет того, что положение снимаемой точки местности в плане и по высоте определяется одним наведением прибора на точку. При использовании данных приборов сущность съемки состоит в определении координат точек местности и нанесении их на карту или план. Преимущество тахеометров также состоит в том, что процесс съемки может быть автоматизирован с использованием электронных тахеометров и составлении цифровой модели местности с применением программных комплексов. Большинство современных тахеометров оборудованы вычислительным и запоминающим устройствами, позволяющими сохранять измеренные или проектные данные, вычислять координаты точек, недоступных для прямых измерений, по косвенным наблюдениям, и т. д. Некоторые современные модели дополнительно оснащены системой GPS (например, LeicaSmartStation).

Устройство электронного тахеометра подробно рассмотрим на примере SOKKIA SET 610.

Рисунок 2. Устройство электронного тахеометра SOKKIA SET 610.

1 – ручка:2 – закрепительный винт:3 – метка высоты инструмента:4 – слот для батареи:5 – разъем ввода/вывода данных:6 – подъемный винт:7 – основание трегера:8 – грубый визир:

9 – фокусирующее кольцо зрительной трубы:10 – окуляр зрительной трубы:11 – диоптрийное кольцо оптического центрира:12 – крышка сетки нитей оптическогоцентрира:13 – окуляр оптического центрира:

14 – защелка трегера:15 – паз для установки буссоли:16 – наводящий винт вертикального круга:17 – закрепительный винт вертикального круга :18 –наводящий винт горизонтального круга :19 – закрепительный винт горизонтального круга :20 – объектив:21 – цилиндрический уровень:

22 – юстировочные винты цилиндрического уровня:23 – панель.

№ точки	Горизонтальный угол(β)			Дирекционный угол (α)	Румб (r)	Горизонтальное проложение (d), м	Приращение координат					Координаты точки, м			№ точки
	Измеренный	исправленный					вычисленный		исправленный
							Δx	Δy	Δx	Δy	x		y
1	+ 1^’ 83^◦ 14’	83^◦ 15’		175^◦	ЮВ 5^◦	620,49	- -0,42 618,13	+ -0,06 54,1	- 618,55	+ 54,04	170		-170	1
2	109^◦ 01’	109^◦ 01’		245^◦ 59’	ЮЗ 65^◦59^’	564,76	- -0,39 229,62	- -0,05 515,85	- 229,91	- 515,90	- 448,55		- 115,96	2
3	101^◦ 47’	101^◦ 47’		324^◦ 12’	СЗ 35^◦ 48’	806,10	+ -0,55 653,82	- -0,07 471,56	+ 653,27	- 471,63	- 678,46		- 631,86	3
4	+1^’ 65^◦ 56’	65^◦ 57’		78^◦ 15’	СВ 78^◦15^’	953,50	+ -0,65 195,84	+ -0,08 933,57	+ 195,19	+ 933,49	- 25,19		- 1103,49	4
Итого	β=359^◦ 58’		β=360^◦	175^◦		2944,85	2,01	0,26	0	0	170		-170

Таблица - Ведомость вычисления точек теодолитного хода

5.3 Обработка результатов теодолитной съемки.

По результатам измерений в первую очередь вычисляют прямоугольные координаты точек поворотов границы участка. Координаты точек вычисляют в специальной ведомости.

Обработка результатов съемки начинается с определения угловой невязки. Подсчитывают в графе 2 сумму измеренных углов и вычисляют угловую невязку хода

где βт - теоретическая сумма углов хода, которую вычисляют по формулам:

βт = 180° (п - 2) - для замкнутого полигона: п - число сторон хода.

βт= 180° (4 - 2)= 360°

βимер= 359°58’

Невязку, полученную по формуле, сравнивают с допустимой

В нашем случаи допустимая невязка равна: ƒβ= ±1,5*√4=±3

Угловая невязка меньше допустимой, ее распределяют на все углы поровну. Поправку d_b, которую вычисляют по формуле

d_b = -f_b/n,

Если f_b не делится без остатка на n, то большую по абсолютной величине поправку вводят в углы с короткими сторонами.

В теодолитных ходах небольшой длины поправки в измеренные углы можно вводить так, чтобы углы оказались округленными до целых минут.

По исправленным значениям углов вычисляем дирекционные углы сторон хода:

a_i_+
1 = a_i + b - 180°

В моем примере исходный дирекционный угол равен 55°:

α2= 175°-19°40’+180°=245°59’

α3= 245°59’-101°47’+180°=324°12’

α4= 324°12’-65°57’+180°=438°15’-360°=78°15’

Проверка: α1= 78°15’-83°15’+180°=415°=175°

В нашем случаи выписывают румбы сторон и определяем знаки приращения координат по таблице.

Таблица -Знаки приращений координат в зависимости от четверти названия румба

Четверть	Название	∆x	∆y
I	СВ	+	+
II	ЮВ	-	+
III	ЮЗ	-	-

r1= 180°-175°=5° ЮВ

r2= 245°59’-180°=65°59’ ЮЗ

r3= 360°-324°12’=35°48’ CЗ

r4= 78°15’ СВ

Вычисляем приращение координат ∆х и ∆y.

∆х=cos5°*620,49=618,13м

∆y=sin5°*620,49=54,1м

∆ x=cos65°59’*564,76=515,856м

∆ y=sin65°59’*564,76=229,52м

∆ x=cos35°48’*806,10=653,62 м

∆ y=sin35°48’* 806,10=471,56 м

∆ x=cos78°15’*953,50=195,84м

∆ y=sin78°15’*953,50=933,57м

Сумма всех значений ∆х=2,01

Сумма всех значений ∆y=0,26

Знаки приращения координат зависят от значения угла a или названия румба. Так, ∆х имеет положительный знак при углах a от 0° до 90° (СВ) и от 270° до 360° (СЗ), a ∆y имеет положительный знак при углах а от 0 до 180°, т.е. (СВ и ЮВ). Во всех остальных случаях приращения ∆х и ∆у имеют знак минус.

Невязку определяют по формуле:

считается допустимой, если она не превышает 1:2000 периметра Р.

ƒp=√(2,01)²+(0,26)²=2,02мм

ƒот=2,02/2944,85=0,0006

ƒ/P=1:2000

6. В нашем примере невязка допустима, то невязку по осям f_x и f_ураспределяем с обратным знаком на все приращения пропорционально длинам горизонтальных проложений. Поправки в приращения координат вычисляют по формулам