
- •__Кинематика и динамика манипулятора с двумя степенями свободы__
- •Пояснительная записка
- •Механика автоматических устройств
- •1. Кинематика плоского механизма с двумя степенями свободы по заданному движению одной из точек
- •2. Кинематика управляемого движения манипулятора
- •3. Динамика механизма с двумя степенями свободы
3. Динамика механизма с двумя степенями свободы

Требуется:
1. Составить уравнения кинетостатики для определения управляющих моментов, реализующих заданное программное движение груза.
2. Составить кинематические уравнения, определяющие изменение во времени угловых скоростей, углов поворота звеньев и скорости точки С.
3.
Решить полученные уравнения на ЭВМ на
интервале времени 0,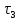 .
.
4.
Построить графики МB, MD, ,
, ,
, ,
, ,
, .
.
5.
Для момента времени
 определить с помощью графоаналитического
метода угловые скорости звеньев, скорость
точки С и сравнить с результатами счета
на ЭВМ.
определить с помощью графоаналитического
метода угловые скорости звеньев, скорость
точки С и сравнить с результатами счета
на ЭВМ.
6. По данным счета найти мощность каждого двигателя при t=0,02.
Манипулятор
перемещает точечный груз массы m за
время
 из точкиdв точкуес заданной
скоростью VМx=0,
VMy=Vsin(kt). Управляющие
двигатели расположены в шарнирах B и D.
из точкиdв точкуес заданной
скоростью VМx=0,
VMy=Vsin(kt). Управляющие
двигатели расположены в шарнирах B и D.
Дано:
DA=2AB=2R1=0,86
м;CP=0,5R1=0,215
м;AC=R3=0,79
м;BD= R1=0,43
R1=0,43 =0,75
м;MB=R2=0,98
м;
=0,75
м;MB=R2=0,98
м; =0,31
рад;
=0,31
рад;
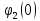 =2,91
рад;
=2,91
рад; =0,41
рад; τ3=0,24 с;V3=3,14
м/с;k=13,1 рад/с;m=11
кг; Δt=0,01 с.
=0,41
рад; τ3=0,24 с;V3=3,14
м/с;k=13,1 рад/с;m=11
кг; Δt=0,01 с.
Массой элементов конструкции и приводов можно пренебречь.
Составляем уравнения кинетостатики для управляющих моментов:
а)
б)
в)
г)

Для
составления уравнений кинетостатики
система освобождается от связей. На
рисунках изображаются реакции связей,
активные силы (сила G)
точки М и внутренние моменты управления
МBz,
MDz.
По принципу Даламбера условно
прикладываются к точке М силы инерции:
сила инерции
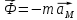 .
Для заданного движения эта сила в
проекциях определяется так:
.
Для заданного движения эта сила в
проекциях определяется так:


Составляем уравнения равновесия систем сил, указанных на рис. а, б, в, г.
Для звена 1 (рис. а):


 (20)
(20)
 (21)
(21)
Для звена 2 (рис. б):


 (22)
(22)
Для звена 3 (рис. в):

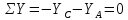
 (23)
(23)
Для звена 4 (рис. г):


Так как
 ,
то
,
то .
.
Так как
 ,
то
,
то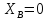 .
.
Так как
 ,
то
,
то .
.
Так как
 и
и ,
то
,
то .
.
То есть:




Из (23)
находим, что

Из уравнений (20) и (22)
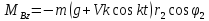

 Составляем
кинематические уравнения. Кинематические
уравнения заимствуются из ранее решенных
задач и с учетом того, что VMx=0
и VMy=Vsin(kt),
запишутся:
Составляем
кинематические уравнения. Кинематические
уравнения заимствуются из ранее решенных
задач и с учетом того, что VMx=0
и VMy=Vsin(kt),
запишутся:




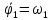

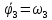
Решаем
систему на интервале времени
 с шагом Δt.
Сведём полученные данные в таблицу:
с шагом Δt.
Сведём полученные данные в таблицу:
|
шаг |
|
|
|
|
|
|
|
|
|
|
0 |
0,31 |
2,91 |
0,41 |
0 |
0 |
0 |
0 |
536,508 |
-137,556 |
|
1 |
0,31 |
2,91 |
0,41 |
0,245208 |
-0,24768 |
-0,28444 |
0,134273 |
532,81 |
-136,608 |
|
2 |
0,314904 |
2,905046 |
0,404311 |
0,488441 |
-0,49061 |
-0,5658 |
0,262866 |
521,1637 |
-133,778 |
|
3 |
0,317356 |
2,90257 |
0,401467 |
0,723808 |
-0,72504 |
-0,83786 |
0,386127 |
502,7094 |
-129,116 |
|
4 |
0,319808 |
2,900093 |
0,398622 |
0,94778 |
-0,94686 |
-1,09637 |
0,501148 |
477,4582 |
-122,702 |
|
5 |
0,32226 |
2,897616 |
0,395778 |
1,156445 |
-1,15229 |
-1,33682 |
0,60604 |
445,8501 |
-114,646 |
|
6 |
0,324712 |
2,895139 |
0,392933 |
1,346137 |
-1,33784 |
-1,55504 |
0,699116 |
408,4339 |
-105,087 |
|
7 |
0,327165 |
2,892663 |
0,390089 |
1,513506 |
-1,50036 |
-1,74719 |
0,778919 |
365,8571 |
-94,1869 |
|
8 |
0,329617 |
2,890186 |
0,387245 |
1,65557 |
-1,6371 |
-1,90988 |
0,844245 |
318,855 |
-82,1346 |
|
9 |
0,332069 |
2,887709 |
0,3844 |
1,769772 |
-1,74573 |
-2,04025 |
0,894159 |
268,238 |
-69,1364 |
|
10 |
0,334521 |
2,885232 |
0,381556 |
1,854029 |
-1,82444 |
-2,13594 |
0,928011 |
214,8774 |
-55,4155 |
|
11 |
0,336973 |
2,882756 |
0,378711 |
1,906762 |
-1,87188 |
-2,19522 |
0,945442 |
159,6905 |
-41,2072 |
|
12 |
0,339425 |
2,880279 |
0,375867 |
1,926933 |
-1,88727 |
-2,21696 |
0,946386 |
103,6247 |
-26,7554 |
|
13 |
0,341877 |
2,877802 |
0,373022 |
1,914059 |
-1,87036 |
-2,20069 |
0,931068 |
47,64124 |
-12,3079 |
|
14 |
0,344329 |
2,875325 |
0,370178 |
1,868228 |
-1,82145 |
-2,14658 |
0,899995 |
-7,30137 |
1,887384 |
|
15 |
0,346781 |
2,872848 |
0,367333 |
1,790095 |
-1,74139 |
-2,05545 |
0,853945 |
-60,2637 |
15,58711 |
|
16 |
0,349233 |
2,870372 |
0,364489 |
1,680874 |
-1,63156 |
-1,92877 |
0,793947 |
-110,342 |
28,55637 |
|
17 |
0,351685 |
2,867895 |
0,361645 |
1,542321 |
-1,49385 |
-1,76863 |
0,721259 |
-156,682 |
40,5729 |
|
18 |
0,354137 |
2,865418 |
0,3588 |
1,376705 |
-1,33061 |
-1,57769 |
0,637345 |
-198,496 |
51,43081 |
|
19 |
0,35659 |
2,862941 |
0,355956 |
1,18677 |
-1,14464 |
-1,35915 |
0,543842 |
-235,075 |
60,94416 |
|
20 |
0,359042 |
2,860465 |
0,353111 |
0,975688 |
-0,93912 |
-1,11669 |
0,442533 |
-265,8 |
68,95015 |
|
21 |
0,361494 |
2,857988 |
0,350267 |
0,74701 |
-0,71755 |
-0,85442 |
0,335308 |
-290,154 |
75,31187 |
|
22 |
0,363946 |
2,855511 |
0,347422 |
0,504602 |
-0,48374 |
-0,57679 |
0,224131 |
-307,73 |
79,92069 |
|
23 |
0,366398 |
2,853034 |
0,344578 |
0,252582 |
-0,24166 |
-0,28853 |
0,111005 |
-318,238 |
82,69813 |
|
24 |
0,36885 |
2,850558 |
0,341734 |
-0,00475 |
0,004536 |
0,005423 |
-0,00207 |
-321,509 |
83,59712 |
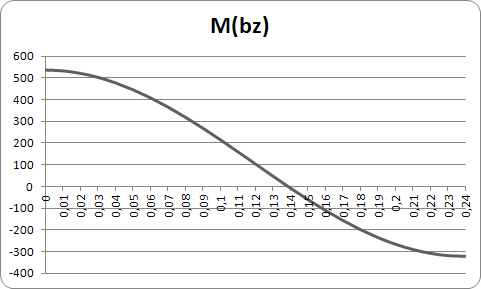
По
результатам решения строим графики
 ,
, ,
, ,
, ,
, ,
, ,
, :
:






Проводим проверку. Извлекаем из таблицы значения углов поворота звеньев из строки под номером 3. Механизм строим в масштабе 1:10, определяем положение мгновенных центров скоростей. Строим векторы скоростей точек A, B, C, M и указываем дугами направления вращения звеньев. По известным значениям скоростей и расстояниям до мгновенных центров скоростей определяем значения угловых скоростей звеньев и скорость точки С.




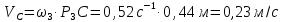
Результаты, полученные с помощью графических построений, близки к результатам решения задачи на ЭВМ и не отличаются более чем на 5%.
Вычисление мощности двигателей управления для t=0,02 c.
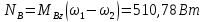

Вывод:кинематический анализ схемы манипулятора с двумя степенями свободы позволил найти уравнения движения звеньев и величины линейных и угловых скоростей при заданном движении одной из точек или при управляемом движении манипулятора, а графоаналитический анализ позволил подтвердить правильность аналитических расчётов. Силомоментный анализ позволил определить реакции связей звеньев и моменты управления, а также мощности двигателей управления для выполнения поставленной задачи, а графоаналитический анализ позволил подтвердить правильность расчётов.

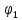 ,
рад
,
рад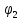 ,
рад
,
рад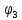 ,
рад
,
рад ,
рад/с
,
рад/с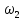 ,
рад/с
,
рад/с ,
рад/с
,
рад/с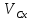 ,
м/с
,
м/с ,
Н*м
,
Н*м ,
Н*м
,
Н*м