
- •Гоу Санкт-Петербургский государственный политехнический университет
- •2. Несущие конструкции здания.
- •3.3 Армирование плитной части.
- •3.4. Расчет усилий и армирование поперечной диафрагмы
- •3.4.1. Подбор поперечной арматуры диафрагмы
- •3.5.Расчет усилий и подбор арматуры в продольных ребрах
- •3.6.Схема армирования продольных ребер
- •3.7. Расчет трещиностойкости продольных ребер.
- •3.7.1. Расчет продольных ребер по образованию трещин.
- •3.7.2. Расчет продольных ребер по раскрытию трещин.
- •4. Расчёт усилий в элементах поперечной рамы каркаса.
- •5. Армирование колонны
- •5.1. Назначение поперечных сечений колонны
- •5.2. Подбор арматуры в расчетных сечениях
- •5.3. Конструирование арматуры
- •6. Конструирование и расчёт фундамента
- •6.1. Конструирование фундамента
- •6.2. Определение напряжений под подошвой фундамента
- •6.3. Расчет фундамента на продавливание
- •6.4. Армирование фундамента
3.5.Расчет усилий и подбор арматуры в продольных ребрах

Рис.8. Схема загружения продольного ребра
Продольные ребра рассматриваются, как свободно опертые балки. Нагрузки на них передается непосредственно от плиты по закону треугольника. Практически нагрузку принимают равномерно распределенной:

где,
g и р – временная и постоянная расчетные нагрузки на 1м2 (см. Таблицу сбор нагрузок);
 -
собственный вес 1п.м. ребра.
-
собственный вес 1п.м. ребра.

где
 - высота продольного ребра;
- высота продольного ребра;
 - средняя ширина
ребра
- средняя ширина
ребра
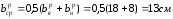 ;
;
 -
объемный вес тяжелого бетона
-
объемный вес тяжелого бетона
 ;
;
 -
коэффициент надежности по нагрузке.
-
коэффициент надежности по нагрузке.
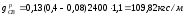

Наибольший изгибающий момент в середине пролета:

Наибольшая поперечная сила на опорах:

где,
 - расчетный пролет
ребра принимается равным, расстоянию
между осями диафрагм:
- расчетный пролет
ребра принимается равным, расстоянию
между осями диафрагм:
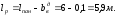
При расчете арматуры в ребре необходимо учесть работу плит, часть которой попадает в сжатую зону. Поэтому профиль сечения ребра представляет собой полутавр с шириной полки:


Рис.9. Профиль сечения ребра
Расчетный профиль будет зависеть от положения нейтральной оси, которое устанавливается проверкой условия:

где,

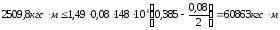
Условие выполняется,
и площадь поперечной арматуры подбирается
как для прямоугольного сечения шириной
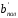 :
:


Принимаем верхний
стержень Ø10-А-400,
 ,
нижний - Ø16-А-400,
,
нижний - Ø16-А-400, .
.
3.6.Схема армирования продольных ребер
Для экономии
металла рекомендуется предусмотреть
обрыв стержней. Обрыв стержней назначается
в соответствии с эпюрами изгибающих
моментов. Для этого на арматурном чертеже
ребра строится так называемая эпюра
материалов, представляющая собой эпюру
моментов
 ,
которые может воспринять ребро имеющимся
в сечении количеством арматуры. Для
построения эпюры материалов воспользуемся
формулой:
,
которые может воспринять ребро имеющимся
в сечении количеством арматуры. Для
построения эпюры материалов воспользуемся
формулой:
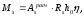
где
 - табличный коэффициент, определяемый
по фактическому проценту армирования
- табличный коэффициент, определяемый
по фактическому проценту армирования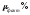


Рис.10. Эпюра материалов при армировании сварными каркасами.
При построении эпюры материалов считают, что обрываемый стержень необходимо завести за точку теоретического обрыва, где он уже не нужен по расчету, для бетона B25 длина анкеровки w:

Продольное ребро армируем одним плоским сварным каркасом, который состоит из двух рабочих стержней продольной арматуры Ø10-А400 и Ø16-А400, поперечных стержней – хомутов Ø6-А-400 с шагом S=100 мм и конструктивного стержня, диаметр которого назначается из конструктивных соображений:

3.7. Расчет трещиностойкости продольных ребер.
3.7.1. Расчет продольных ребер по образованию трещин.
Расчет железобетонных элементов по трещинообразованию выполняют на действие нормативных нагрузок.

где
 и
и временная и постоянная нормативные
нагрузки на 1м2
(см. Таблицу сбор нагрузок);
временная и постоянная нормативные
нагрузки на 1м2
(см. Таблицу сбор нагрузок);

где
 - высота продольного ребра;
- высота продольного ребра;
 - средняя ширина
ребра
- средняя ширина
ребра
 ;
;
 -
объемный вес тяжелого бетона
-
объемный вес тяжелого бетона
 ;
;
 -
коэффициент надежности по нагрузке.
-
коэффициент надежности по нагрузке.


Расчет железобетонных элементов по образованию нормальных трещин производится из условия:

Условие не выполняется, трещины образуются.
где: Мr момент внешних сил;
Мcrc — момент, воспринимаемый сечением, определяемый по формуле:
 ,
,
где:
 -
расчетное сопротивление бетона осевому
растяжению (по второй группе предельных
состояний);
-
расчетное сопротивление бетона осевому
растяжению (по второй группе предельных
состояний);
Wpl упруго пластический момент сопротивления приведенного сечения для крайнего растянутого волокна с учетом неупругих деформаций растянутого бетона;

где Wred момент сопротивления для растянутой грани приведенного сечения, определяемый по правилам сопротивления упругих материалов.
- коэффициент для прямоугольных сечений принимается равным 1,75.

где
 - приведенный момент инерции относительно
оси х-х, проходящей через центр тяжести
сечения;
- приведенный момент инерции относительно
оси х-х, проходящей через центр тяжести
сечения;
 -
расстояние от максимально удаленной
грани сечения до центра тяжести сечения.
-
расстояние от максимально удаленной
грани сечения до центра тяжести сечения.

Рис. 11
Положение оси х-х определяется по формуле:

где
 - площадь приведенного сечения:
- площадь приведенного сечения:

где
 - площадь полки приведенного сечения;
- площадь полки приведенного сечения;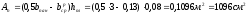
 - площадь ребра
приведенного сечения;
- площадь ребра
приведенного сечения;

 - площадь рабочей
арматуры;
- площадь рабочей
арматуры;
 -
площадь конструктивной арматуры;
-
площадь конструктивной арматуры;
 -
коэффициент привидения бетона к арматуре
-
коэффициент привидения бетона к арматуре



где



 - расстояния от нижней грани сечения
(оси 0-0) до центра тяжести приведенных
сечений;
- расстояния от нижней грани сечения
(оси 0-0) до центра тяжести приведенных
сечений;
 ;
;






где:
 - момент инерции полки;
- момент инерции полки;
 - момент инерции
ребра;
- момент инерции
ребра;



 - расстояния от
центров тяжести приведенных сечений
до оси х-х проходящей через центр тяжести
всего сечения;
- расстояния от
центров тяжести приведенных сечений
до оси х-х проходящей через центр тяжести
всего сечения;


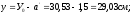



Напряжения, возникающие в растянутой зоне:

 -
условие прочности не выполняется,
поэтому необходимо выполнить расчет
ребра по раскрытию трещин.
-
условие прочности не выполняется,
поэтому необходимо выполнить расчет
ребра по раскрытию трещин.
