Липецкий государственный технический университет

Кафедра автоматизированных систем управления

КУРСОВАЯ РАБОТА

по компьютерной графике

Построение кривых Безье

Студент _______________ Лакомов С. Л.

^{подпись, дата}

Группа АС-11

Руководитель

к. т. н., доцент _______________ Назаркин О. А.

^{подпись, дата}

Липецк 2012 г.

АННОТАЦИЯ

С. 15. Ил. 6. Источники 3 назв.

В данной работе представлена математическая модель построения кривых Безье с описанием реализации на языке Visual С++.

ОГЛАВНЕНИЕ

1 Математическая модель 3

1.1 Определение кривой Безье. 3

1.2 Частные случаи кривой Безье 4

1.3 Вычисление длины кривой 5

1.4 Условие непрерывности соседних кривых Безье 5

2 Описание алгоритмов 8

2.1 Построение кривой по четырем заданным точкам 8

2.2 Построение составной кривой 8

2.3 Выбор пользователем точки на составной кривой 8

3 Описание структуры ПО 9

3.1 Структура ПО 9

5 Контрольный пример 12

1 Математическая модель

1.1 Определение кривой Безье.

Кривая Безье — параметрическая кривая, задаваемая выражением

где  — функция компонент векторов опорных вершин, а  — базисные функции кривой Безье.

,

где  — число сочетаний из  по , где  — степень полинома,  — порядковый номер опорной вершины.

1.2 Частные случаи кривой Безье

1.2.1 Линейные кривые

При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P₀ и P₁ определяют его начало и конец. Кривая задаётся уравнением:

.

1.2.2 Квадратичные кривые

Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P₀, P₁ и P₂.

.

1.2.3 Кубические кривые

В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

.

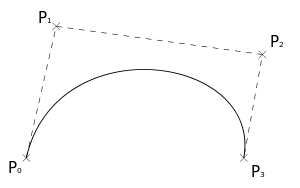
Рисунок 1. Кубическая кривая Безье.

Четыре опорные точки P₀, P₁, P₂ и P₃, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P₀ направляясь к P₁ и заканчивается в точке P₃ подходя к ней со стороны P₂. То есть кривая не проходит через точки P₁ и P₂, они используются для указания её направления. Длина отрезка между P₀ и P₁ определяет, как скоро кривая повернёт к P₃.

Квадратичная кривая Безье с координатами   преобразовывается в кубическую кривую Безье с координатами 

1.3 Вычисление длины кривой

Длина кубической кривой, заданной четырьмя точками , приближается ломаными по формуле:

(1)

1.4 Условие непрерывности соседних кривых Безье

Пусть кривая Безье  степени  задана вершинами , а соседняя кривая Безье  степени  - вершинами . Тогда непрерывность первой производной в точке соединения выражается соотношением

, где  - скаляр.

Рисунок 2. Непрерывность  первой производной для кубических кривых Безье.

Вычисление  -й производной при :

и при :

.

Отсюда первые производные в концах будут

     и .                     

 Это показывает, что касательные к кривой Безье в первой и последней точках параллельны соответствующим сторонам многоугольника.

Пользуясь уравнениями получим . Из непрерывности кривой следует, что  и .

Отсюда направления касательных на стыке совпадают, если три вершины , ,  коллинеарны, т.е.  должна лежать на линии между  и .

Если совпадают еще и величины касательных векторов, то  является серединой отрезка от  до :

или

.

На рисунке 2 приведена иллюстрация для , т. е. для двух кубических кривых Безье.

Кубическая кривая Безье задается в виде

,      (2)

где  , , , ,  - определяющие вершины.

Тогда многоугольник  , , ,  определяет кривую Безье ,, соответствующую первой половине исходной кривой, а именно ,. Подобным образом, многоугольник , , ,  определяет кривую Безье , , соответствующую второй половине исходной кривой, т.е. , . Новые определяющие вершины многоугольника  и  получаются путем приравнивания радиус-векторов и касательных векторов при , ; ,  и , ; , . Получаем

,

,

,

.

Решение этих уравнений дает

,        ,               

,            .