1ПОСТАНОВКА ЗАДАЧИ 4

Дано уравнение: 4

2ОПИСАНИЕ АЛГОРИТМОВ 5

МЕТОД ДЕЛЕНИЯ ОТРЕЗКА ПОПОЛАМ 5

МЕТОД ХОРД 5

МЕТОД НЬЮТОНА 6

МЕТОД ИТЕРАЦИЙ 7

3ПЕРЕЧЕНЬ ИДЕНТИФИКАТОРОВ 9

4 КРАТКОЕ ОПИСАНИЕ ПРОГРАММЫ 10

После нажатия кнопки ОК пользователь увидит на форме таблицу с 12

результатами работы программы и 4 графика, соответствующие заданию: 12

5.1 БЛОК-СХЕМЫ ПРОЦЕДУР 14

5.1.1 iteration 14

14

5.1.2 newton 15

5.1.3 HalfDivide 16

16

5.1.4 Chordes 17

17

6 ПРОВЕРКА СЧЕТА ПО ПРОГРАММЕ 18

ЗАКЛЮЧЕНИЕ 19

ЛИСТИНГ ПРОГРАММЫ 20

1 ПОСТАНОВКА ЗАДАЧИ3

2 ОПИСАНИЕ АЛГОРИТМОВ4

3 ПЕРЕЧЕНЬ ИДЕНТИФИКАТОРОВ 8

4 КРАТКОЕ ОПИСАНИЕ ПРОГРАММЫ 9

5 БЛОК-СХЕМА АЛГОРИТМА 12

5.1 БЛОК-СХЕМЫ ПОЦЕДУР 13

5.1.1 iteration13

5.1.2 Newton14

5.1.3 HalfDivide15

5.1.4 Chordes16

6 ПРОВЕРКА СЧЕТА ПО ПРОГРАММЕ 17

ЗАКЛЮЧЕНИЕ 18

ЛИСТИНГ ПРОГРАММЫ 19

1. Постановка задачи Дано уравнение:

[0,1]

Сравнить методы деления отрезка пополам, хорд, касательных и итераций, поочередно используя их для решения одного и того же уравнения. Независимо от метода заканчивать построения, как только будет получено такое приближение x, для которого |f(x)|< Ɛ, Ɛ = 0,01; 0,001;...10^-7 . Для каждого из методов построить диаграмму и график изменения числа потребовавшихся приближений при переходе от одного значения Ɛ к другому и вывести данные числа в виде таблицы в файл.

2. Описание алгоритмов метод деления отрезка пополам

Пусть дано уравнение f(x)=0, функция f(x) непрерывна на интервале [a,b]. Условие f(a)* f(b)<0 указывает тогда на наличие хотя бы одного корня на этом отрезке.

Поделим отрезок [a,b] пополам точкой c, координата которой c=(a+b)/2 и вычислим значение функции f(c).

Возможны два случая:

а) f(a)*f(c)>0, т.е. значения функции на концах отрезка [a, c] одинаковы по знаку; тогда корень уравнения находится на отрезке [c, b] и отрезок [a, c] можно исключить из дальнейшего рассмотрения, перенеся точку a в точку c: a=c; f(a)=f(c) (рис. а);

б) f(a)*f(c)<0, т.е. значение функции на концах отрезка [a, c] противоположны по знаку; тогда корень находится на отрезке [a, c] и отрезок [c, b] можно исключить из дальнейшего рассмотрения, перенеся точку b в точку c: b=c (рис. б).

После исключения правой или левой половины отрезка продолжают деление пополам до тех пор, пока длина оставшегося интервала [a, b] не станет меньше некоторой заданной малой величины Ɛ , т.е. |b-a| <Ɛ , и тогда любое значение аргумента из отрезка [a, b] можно считать корнем с погрешностью Ɛ .

Метод хорд

Нелинейная функция f(x) на отделенном интервале [а,b] заменяется линейной, в качестве которой берется хорда – прямая, стягивающая концы нелинейной функции. Эта хорда определяется как прямая, проходящая через точки с координатами (а,f(а)) и (b,f(b)). Имея уравнение хорды: у = cx + d, можно легко найти точку ее пересечения с горизонтальной осью, подставив в уравнение у = 0 и найдя из него x. Естественно, в полученной таким путем точке x₁ не будет решения, ее принимают за новую границу отрезка, где содержится корень. Через эту точку с координатами (x₁,f(x₁)) и соответствующую границу предыдущего интервала опять проводят хорду, находят x₂ и т. д. несколько раз, получая последовательность: х₃, х₄, х₅ ..., сходящуюся к корню.

Алгоритм метода зависит от свойств функции f(х). Если f(b) f"(b)>0, то строящаяся на каждом этапе хорда имеет правый фиксированный конец и тогда алгоритм будет выглядеть так:

при этом последовательность х₁, х₂, х₃... будет приближаться к корню слева.

Если f(a) f''(a) > 0, то строящаяся при каждом этапе хорда имеет левый фиксированный ("закрепленный") конец и алгоритм выглядит следующим образом:

при этом последовательность х₁, х₂, ... будет приближаться к корню справа.

Условием прекращения пополнения последовательности является: |х_i+1 –х_i| <Ɛ

Метод ньютона

Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только в качестве прямой берется касательная, проводимая в текущей точке последовательности. Уравнение касательной находится по координате одной точки и углу наклона (значение производной). В качестве начальной точки в зависимости от свойств функции берется или левая точка: x₀ = а (если f(а) f"(a) > 0), или правая точка: x₀ = b (если f(b) f"(b)>0).

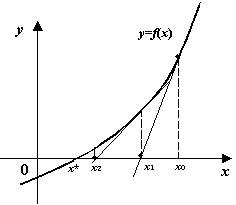
Алгоритм записывается следующим образом:

Условием прекращения пополнения последовательности является: |х_i+1 –х_i| <Ɛ