Распределение Стьюдента

Распределение Стьюдента (t- распределение) имеет важное значение при статических вычислениях, связанных с нормальным законом, а именно тогда, когда среднеквадратичное отклонение не известно и еще подлежит определению по опытным данным.

Пусть X и X1, X2, …Xn – независимые случайные величины, имеющие нормальное распределение с параметрами:

M[X] = M[X1] = M [X2] = … = M[Xn] = 0

И

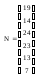
Случайная величина:

являющаяся функцией нормально распределенных случайных величин, называется безразмерной дробью Стьюдента. Распределения случайной величины T не зависит от параметров распределения независимых случайных величин X и X1, X2, …Xn, а зависит только от одного параметра – числа степеней свободы r.

Математическое ожидание и дисперсия случайной величины T соответственно равны:

M[T] = 0 D[T] = 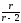r > 2

При неограниченном увеличении числа степеней свободы распределения Стьюдента асимптотически переходит в нормальное распределение Гаусса с параметрами

M[T] = 0 и D[T] = 1.

В математической статистике часто используется квантили распределения Стьюдента в зависимости от числа степеней свободы r и заданного уровня вероятности.

С геометрической точки зрения нахождение квантилей распределения Стьюдента , заключается в таком выборе значения, при котором суммарная площадь под кривой плотностина участкахибыла бы равно.

2.2 Расчеты

Дана выборка:

41,77	41,81	41,64	41,54	41,91	41,67	41,55	41,84	41,61	41,80
42	62	86	65	70	85	60	69	95	62
71	50	76	73	66	43	68	52	70	46
58	89	56	32	53	99	83	35	61	37
95	57	87	75	82	50	41	78	42	98
64	80	65	58	72	80	60	72	70	62
70	92	53	60	74	69	61	55	38	51
82	44	97	78	80	34	70	49	60	63
75	63	70	48	52	73	69	71	78	47
58	74	55	65	78	54	51	68	56	64

Количество интервалов Nint=6

Минимальное и максимальное значение выборки:

Ширина подынтервала:

Граничные точки подынтервалов

Чтобы найти полигон частот отсортируем выборку с помощью функции sort() и запустим цикл для данной выборки.

Проверим данные частоты с помощью функции hist()

Значения верны. Построим гистограмму:

Найдем оценки для математического ожидания и дисперсии:

Для этого найдем середины отрезков данных интервалов

Доверительный интервал для мат.ожидания:

Надёжность равна 0.95

Квантили распределения Стьюдента найденные по таблице:

Левая и правая границы доверительного интервала:

Доверительный интервал для дисперсии при той же надежности:

Квантили распределения Пирсона найденные по таблице:

Левая и правая границы доверительного интервала:

Для того чтобы проверить гипотезу о том, что наша выборка извлечена из нормальной генеральной совокупности, найдем теоретические частоты.

Функция распределения Лапласа

Найденные частоты:

Проверим данную гипотезу с помощью критерия Х2 Пирсона:

По таблице найдем критическую точку для данной выборки при уровне значимости равным 0.05 и степенями свободы равным k:

Где S –количество интервалов, т.е равно 6 и r– количество параметров, для нормального распределения их 2.

Значит, гипотезу о нормальном распределении выборки отвергаем.

2.3. Выводы

В ходе работы над первой частью курсовой работы был написан теоретический обзор по точечному и интервальному оцениванию. В работе выполнены расчеты, связанные с нахождение доверительных интервалов для математического ожидания, дисперсии и вероятности. Для заданной генеральной совокупности построены гистограмма и полигон, найдены оценки математического ожидания и дисперсии, а также доверительные интервалы для математического ожидания и дисперсии. С помощью критерия согласия Пирсона проверена гипотеза о том, что выборка извлечена из нормальной генеральной совокупности. В результате анализа, гипотеза не подтвердилась, т.к. получилось, что. Отсюда следует вывод, что гипотеза о нормальном законе распределения генеральной совокупности должна быть отвергнута.