2.2 Амплитудно-частотная характеристика

Амплитудно-частотная характеристика (АЧХ) — функция, показывающая зависимость модуля некоторой комплекснозначной функции от частоты. Также может рассматриваться АЧХ других комплекснозначных функций частоты, например, спектральной плотности мощности сигнала.

АЧХ в теории линейных стационарных систем означает зависимость модуля передаточной функции системы от частоты. АЧХ показывает, во сколько раз амплитуда сигнала на выходе системы отличается от амплитуды входного сигнала на всём диапазоне частот.

На графике АЧХ по оси абсцисс откладывается частота, а по оси ординат отношение амплитуд выходного и входного сигналов системы. Обычно для частоты используется логарифмический масштаб, так как исследуемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов Гц или рад/с). В случае, когда логарифмический масштаб используется и на оси ординат, АЧХ превращается в логарифмическую амплитудно-частотную характеристику. ЛАЧХ получила широкое распространение в теории автоматического управления в связи с простотой построения и наглядностью при исследовании систем управления.

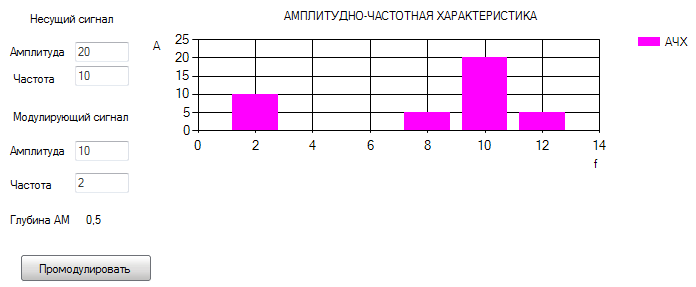
Рисунок 2.2 – Программная реализация амплитудно-частотной характеристики

2.3 Метод суперпозиции

Непосредственный анализ воздействия сигналов сложной формы на радиотехнические цепи весьма затруднителен и вообще не всегда возможен. Поэтому сложные сигналы имеет смысл представлять как сумму некоторых простых элементарных сигналов. Принцип суперпозиции обосновывает возможность такого представления, утверждая, что в линейных цепях воздействие суммарного сигнала равносильно сумме воздействий соответствующих сигналов по отдельности.

В качестве элементарных сигналов часто применяют гармоники. Такой выбор имеет ряд достоинств:

1) Разложение на гармоники реализуется достаточно легко путем использования преобразования Фурье.

2) При воздействии гармонического сигнала на любую линейную цепь его форма не изменяется (остается гармонической). Сохраняется также частота сигнала. Амплитуда и фаза, конечно, изменяются; их можно сравнительно просто рассчитывать, применяя метод комплексных амплитуд.

3) В технике широко используются резонансные системы, позволяющие экспериментально выделять одну гармонику из сложного сигнала.

Представление сигнала суммой гармоник, заданных частотой, амплитудой и фазой, называется разложением сигнала в спектр.

Гармоники, входящие в состав сигнала, задаются в тригонометрической или мнимопоказательной форме.

Рисунок 3.3 – Программная реализация принципа суперпозиции

На рисунке 3.3 показано, что исходный сигнал с амплитудой (A) = 10 и длиной (τ) = 20 может быть представлен двумя другими сигналами, которые размещены от исходного сигнала на указанном расстоянии ) = 200 и отступом (Ω) = 4 от в обе стороны.

2.4 Оцифровка сигнала

Для более удобной передачи данных сигналы следует оцифровывать. Следующая программа оцифровывает случайный сигнал. Входные параметры: Максимальная амплитуда A. Шаг оцифровки: чем он больше, тем крупнее шаги и меньше значений будет обработано и переведено в двоичную систему счисления.

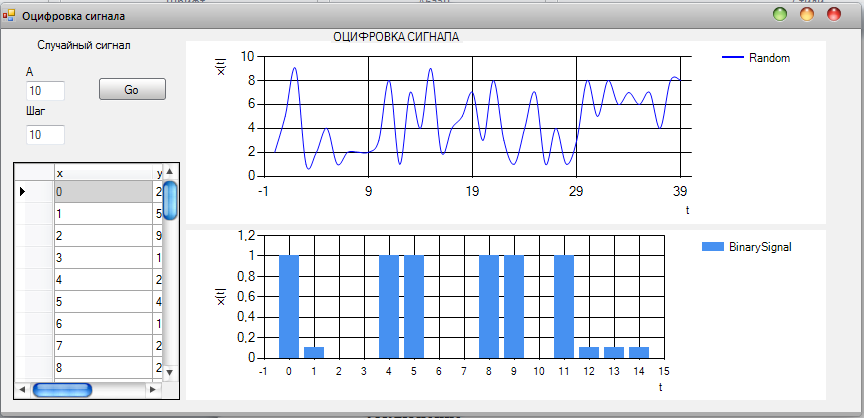
Рисунок 3.4.1 – Результат выполнения оцифровки сигнала

Рисунок 3.4.2 – Результат выполнения оцифровки сигнала

Рисунок 3.4.3 – Результат выполнения оцифровки сигнала

На рисунках 3.4.1 – 3.4.2 показаны результаты выполнения программы, которая оцифровывает сигнал. Из рисунков видно как с изменением параметра «Шаг» меняется нижний график (бинарный сигнал). Чем меньше шаг, тем больше точек сигнала обработчик переводит из десятичной системы счисления в двоичную систему счисления.