
ММСЭС / Analys_DS
.pdf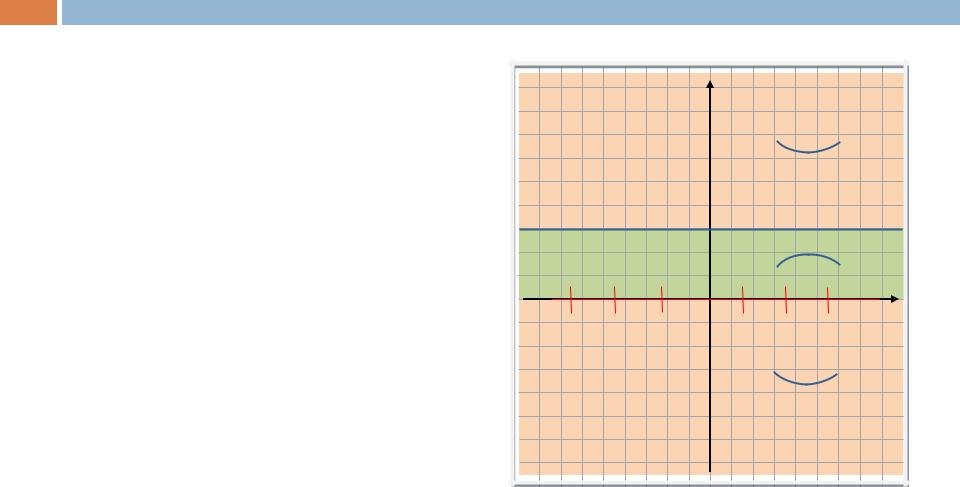
Пример 12.
61
Установим, какой характер выпуклости (вогнутости) имеют фазовые траектории относительно оси x. Для этого найдем производную y”(x):
d 2 y |
|
d |
y 1 |
|
|
d |
|
|
1 |
|
|
y '(x) |
|
y 1 |
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
, |
|||||
dx |
2 |
|
y |
|
|
y |
2 |
y |
3 |
|
|||||||||||
|
|
dx |
|
|
dx |
|
y |
|
|
|
|
|
|
||||||||
и определим области «знакопостоянства» полученного выражения. В тех областях, где y”(x) > 0, фазовые траектории имеют
выпуклость «вниз», а где y”(x) < 0, –
выпуклость «вверх».
y |
y”(x) > 0 |
y”(x) < 0 |
x |
y”(x) > 0 |
Пример 12. |
|
|
|
|
|||||
62 |
|
|
|
|
|
|
|
|
|
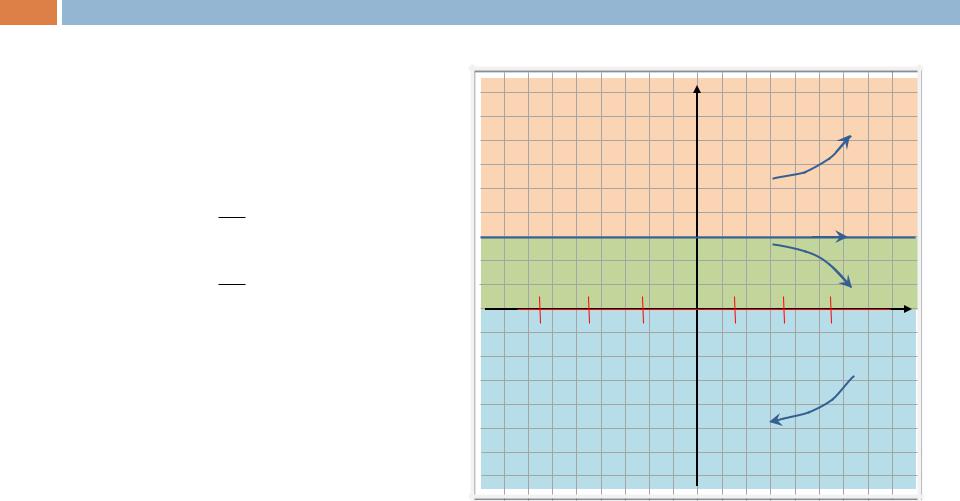
Выясним направления движения по |
|
|
y |
||||||
фазовым |
траекториям, |
определив |
|
|
|||||
|
|
|
|||||||
области «знакопостоянства» правых |
x’(t) > 0, |
y’(t) > 0 |
|
||||||
частей системы |
|
|
|
|
y”(x) > 0 |
|
|||
|
|
dx |
y, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
dy |
y 1. |
|
|
x’(t) > 0, |
y’(t) < 0, |
y”(x) < 0 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
dt |
|
|
|
|
|
|
|
Границами |
этих |
областей |
будут |
|
|
|
|||
вертикальная |
и |
горизонтальная |
x’(t) > 0, |
y’(t) < 0 |
|
||||
изоклины. |
|
|
|
|
|
y”(x) > 0 |
|
||
|
|
|
|
|
|
|
|
||
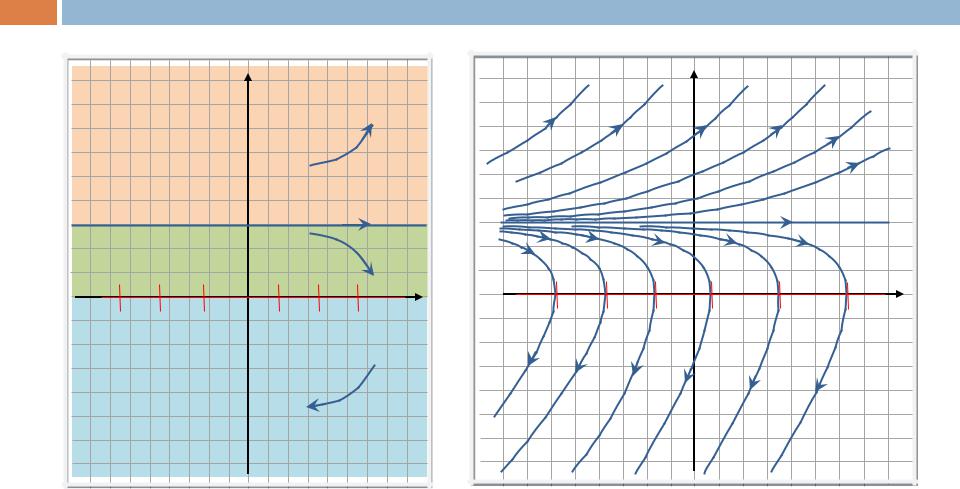
Полученной информации достаточ- |
|
|
|
||||||
но |
для |
построения |
фазового |
|
|
|
|||
портрета. |
|
|
|
|
|
|
|
|
|
Пример 12. |
|
|
|
63 |
|
|
|
|
y |
|
y |
|
|
|
|
x’(t) > 0, |
y’(t) > 0 |
|
|
y”(x) > 0 |
|
|
|
x’(t) > 0, |
y’(t) < 0, |
|
|
y”(x) < 0 |
x |
x |
|
|
|
||
x’(t) > 0, |
y’(t) < 0 |
|
|
y”(x) > 0 |
|
|
|

Пример 13.
64
dx 2,dt
dy 2x y.dt
Горизонтальная изоклина: 2x y = 0.
Выясним, существуют ли прямые, которые содержат фазовые траектории. Уравнения таких прямых будем искать в виде y = kx + b. Так как
k |
dy |
|
|
|
|
2x y |
|
|
|
|
(2 k)x b |
, |
|
|
|
|
|
||||||||
dx |
y kx b |
2 |
|
y kx b |
2 |
|||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
то последнее выражение не зависит от x, если k = 2. Тогда для нахождения b
получим |
|
b |
|
b 4. |
|
2 |
|||||
|
|||||
|
2 |
|
|
||
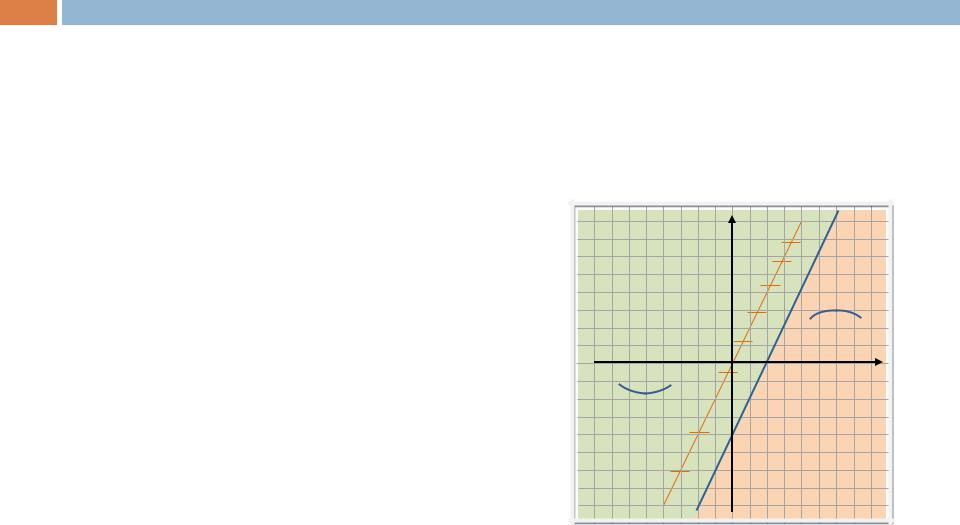
Таким образом, на прямой y = 2x 4 лежат фазовые траектории. Эта прямая является асимптотой на фазовой плоскости.
Пример 13.
65
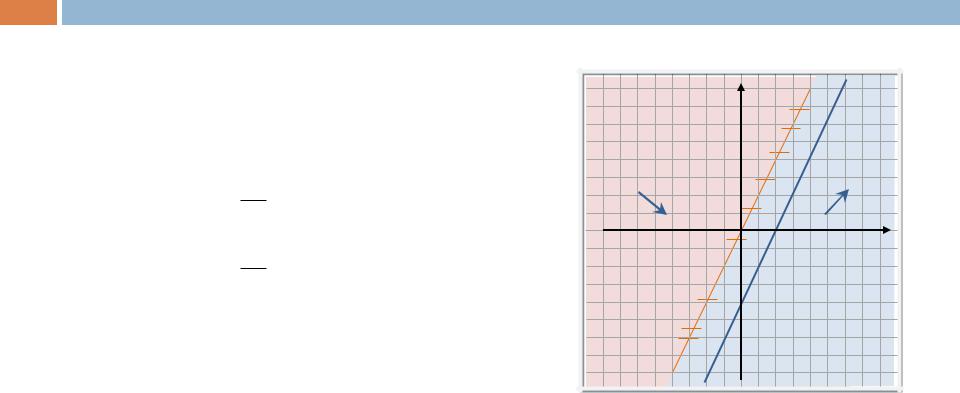
Установим, какой характер выпуклости (вогнутости) имеют фазовые траектории относительно оси x. Для этого найдем производную y”(x):
d 2 y |
|
d |
2x y |
|
2 y '(x) |
|
1 |
|
2 |
|
2x y |
|
y 2x 4 |
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
dx |
2 |
|
|
2 |
2 |
|
4 |
|||||||||||
|
|
dx |
2 |
|
|
|
|
|
2 |
|
|
|||||||
Определим области «знакопостоянства» полученного выражения. В тех областях, где y”(x) > 0, фазовые траектории имеют выпуклость «вниз», а где y”(x) < 0, – выпуклость «вверх».
y
y”(x) > 0
x
y”(x) < 0
Пример 13.
66
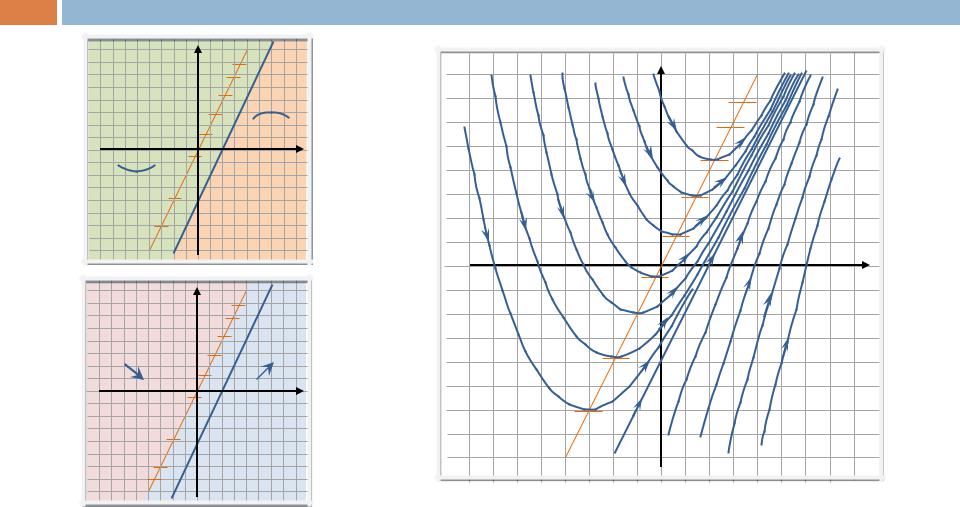
Выясним направление движения по фазовым траекториям, определив области «знакопостоянства» правых частей системы:
dx
dt 2,
dy 2x y.
dt
Границей этих областей будет горизонтальная изоклина.
|
y |
|
x’(t)>0, |
y’(t)<0 |
|
|
|
x |
|
x’(t)>0, |
y’(t)>0 |
Полученной информации достаточно для построения фазового портрета.
Пример 13.
67
y
y”(x) > 0
x
y”(x) < 0
x’(t)>0, |
y |
|
|
y’(t)<0 |
|
|
x |
|
x’(t)>0, |
|
y’(t)>0 |
y
x

Пример 14.
68
dx x y,dt
dy 2(x y) 2.dt
Вертикальная изоклина: x y = 0; горизонтальная изоклина: x y + 1= 0.
Выясним, существуют ли прямые, которые содержат фазовые траектории. Уравнения таких прямых будем искать в виде y = kx + b. Так как
|
dy |
|
|
2(x y) 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||
k |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
dx |
|
y kx b |
x y |
|
y kx b |
|
|
|
x y |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|||||
то последнее выражение не зависит от x, если
получим |
1 |
2 |
|
2 |
|
b 2. |
|
b |
2 |
2 |
, |
|
||
(1 k)x b |
||
y kx b |
|
|
k = 1. Тогда для нахождения b
Таким образом, на прямой y = x +2 лежат фазовые траектории. Эта прямая является асимптотой на фазовой плоскости.
Пример 14.
69
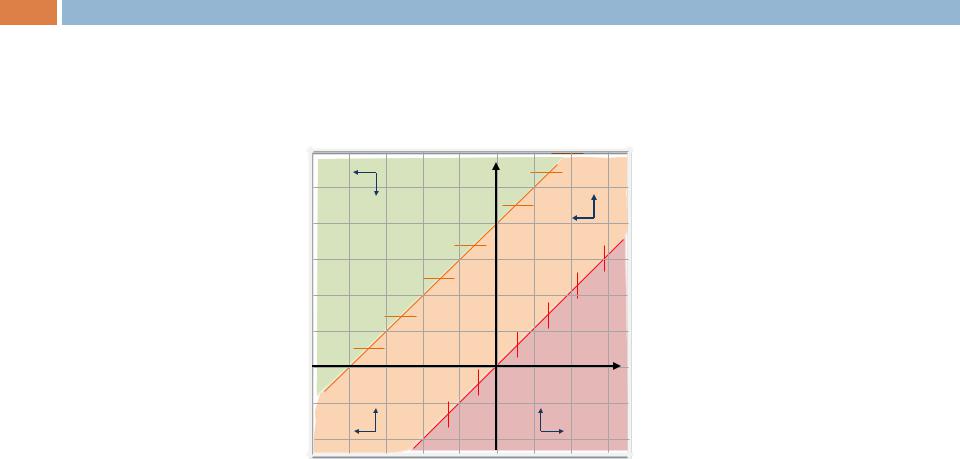
Определим, как изменяются абсцисса и ордината движущейся точки по фазовой траектории. Для этого построим области «знакопостоянства» правых частей системы.
|
y |
|
|
x’(t)<0, |
y’(t)<0 |
|
|
|
x’(t)<0, |
y’(t)>0 |
|
|
|
|
x |
|
|
x’(t)>0, |
y’(t)>0 |
Эта информация потребуется для определения направления движения по траекториям.
Пример 14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
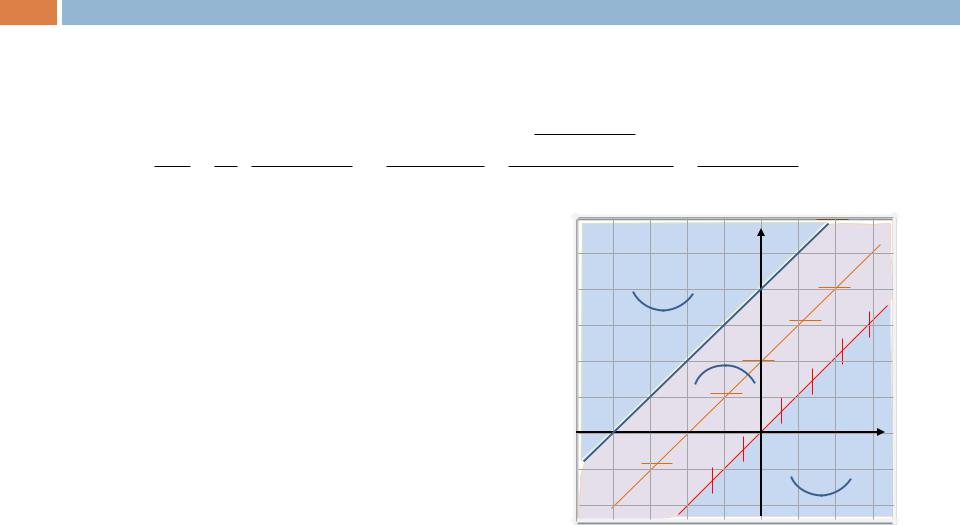
Установим, какой характер выпуклости (вогнутости) имеют фазовые траектории |
||||||||||||||||||
относительно оси x. Для этого найдем производную y”(x): |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2(x y) 2 |
|
|
|
|
|
|
d 2 y |
d |
2(x y) 2 |
|
|
2( y '(x) 1) |
2 |
|
x y |
|
1 |
|
2(x y 2) |
|
|||||
|
|
|
|
|
|
|
||||||||||||
dx |
2 |
|
x y |
|
|
|
(x |
y) |
2 |
|
|
(x y) |
2 |
|
|
(x y) |
3 |
. |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
Определим |
области |
«знакопостоянства» |
|
|
y”(x)> 0 |
|
|
|
||||||||||
полученного выражения. |
|
В тех областях, |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||
где y”(x) > 0, фазовые траектории имеют |
|
|
|
|
|
|
|
|||||||||||
выпуклость |
«вниз», а где y”(x) < 0, – |
|
|
|
|
|
|
|
||||||||||
выпуклость «вверх». |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y”(x)< 0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученной |
информации |
достаточно |
для |
|
|
|
|
|
y”(x)> 0 |
|||||||||
|
|
|
|
|
|
|
||||||||||||
построения фазового портрета. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
