
Министерство образования Российской Федерации
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ВТ и АСУ
Утверждаю:
Зав. кафедрой ВТ и АСУ
д.т.н.проф Ключко В.И.
ЗАДАНИЕ
на курсовое проектирование
Студентки: _Пащенко А.В.______ группы _10-К-ПИ-1__3 курса
факультета КТАС
специальности 080801 Прикладная информатика в экономике
Тема проекта: Исследование эффективного кодирования. Метод Шеннона-Фано
Содержание задания: Исследование эффективного кодирования. Метод Шеннона-Фано
Объем работы:
а) пояснительная записка к проекту ______________.,
б) программы .
Рекомендуемая литература:
1. А.В.Власенко, В.И.Ключко Теория информации и сигналов. Учебное пособие / Краснодар: Изд-во КубГТУ, 2003.- 97 с.
2.Теория передачи сигналов: Учебник для вузов / А.Г.Зюко, Д.Д.Кловский, М.В.Назаров, Л.М.Финк. - 2-е изд., перераб. и доп. - М.: Радио и связь, 1986.
3. Т. А. Павловская. C#. Программирование на языке высокого уровня.Учебник для вузов.ISBN: 978-5-91180-174-8.2009г.
Срок выполнения проекта: с “_10_”_сентября_ по “___”__________ 2012 г.
Срок защиты: “___”_____________2012 г.
Дата выдачи задания: “___”______________2012 г.
Дата сдачи проекта на кафедру: “___”______________2012 г.
Руководитель проекта _ д.т.н.проф Ключко В.И._____________________
(подпись,ф.и.о.,звание,степень)
Задание принял студент _______________________________________
(подпись, дата)
Краснодар
2012
Министерство образования Российской Федерации
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра ВТ и АСУ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту (работе)
по дисциплине ‘‘Теория информации и сигналов’’
на тему ‘‘Исследование квантования сигналов по уровню‘‘
Выполнила студентка __Пащенко Андрей Васильевич_____
группы _10-К-ПИ-1______________________________________
Допущен к защите_______________________________________
Руководитель проекта д.тех.н.проф. Ключко В.И.__________
Нормоконтролер________________________________________
Защищен_____________ Оценка_______________
(дата)
Члены комиссии________________________________________
(подпись,дата,расшифровка подписи)
Краснодар
2012
Министерство образования Российской Федерации
КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Реферат
Пояснительная записка курсовой работы – 19 стр.
Количество рисунков – 2
Количество приложений – 1
Количество источников – 3
Ключевые слова: КОДИРОВАНИЕ, МЕТОД, КОД
Объектом исследования работы является изучение эффективного коддирования.
Цель работы состоит в создании программы для реализации исследования эффективного коддирования.
К полученным результатам относится приложение, демонстрирующее реализацию эффективного кодирования по методу Шеннона – Фано.
Содержание
Введение…………………………………………………………………..5
1.Теоретические сведения .………………………………..………….....6
2.Требования к программному изделию……………………………...12
3.Описание программы………………………………………………....13
4.Результаты и листинг программы……………………...…………....14
Заключение………………………………………………………….……18
Список использованной литературы…………..…….……..…………19
Введение
Роль информации в современном обществе непрерывно возрастает. Информационные процессы являются обязательной составляющей производства, экономики, науки, военного дела и общественной жизни.
В курсовой работе будет исследовано построение эффективного кода по методу Шеннона – Фано.
1.Теоретические сведения
Эффективное кодирование информации
Понятие о кодировании.
Коды появились в глубокой древности в виде, когда ими пользовались для засекречивания важного сообщения. В наше время коды приобрели иное значение, являясь, прежде всего, средством для экономной, удобной и практически безошибочной передачи сообщений. Новое применение кодов сложилось в результате бурного развития средств связи, неизмеримо возросшего объема передаваемой информации. Решать возникшие в связи с этим задачи было бы невозможно без привлечения самых разнообразных математических методов. Неслучайно поэтому теория кодирования считается сейчас одним из наиболее важных разделов прикладной математики.
Как известно, передача информации от источника к получателю производится посредством сигналов. Для того чтобы сигналы были однозначно поняты, их необходимо составлять по правилу, которое строго фиксировано в течение всего времени передачи данной группы сообщений. Правило, устанавливающее каждому конкретному сообщению строго определенную комбинацию различных символов, называется кодом, а процесс преобразования сообщения в комбинацию различных символов или соответствующих им сигналов - кодированием. Процесс восстановления содержания сообщения по данному коду называется декодированием.
Последовательность символов, которая в процессе кодирования присваивается каждому из множеств передаваемых сообщений, называется кодовым словом. Символы, с помощью которых записано передаваемое сообщение, составляют первичный алфавит, а символы, с помощью которых сообщение трансформируется в код - вторичный алфавит.
Исторически первый код, предназначенный для передачи сообщений, связан с именем изобретателя телеграфного аппарата Сэмюэля Морзе и известен всем как азбука Морзе. Другим кодом, столь же широко распространенным в телеграфии, является код Бодо. Оба они используют два различных элементарных сигнала. Такие коды принято называть двоичными.
Коды, в которых сообщения представлены комбинациями с неравным количеством символов, называются неравномерными, или некомплектными. Коды, в которых сообщения представлены комбинациями с равным количеством символов, называется равномерными, или комплектными.
Примером неравномерного кода может служить азбука Морзе, а равномерного - пятизначный код Бодо.
Коды могут быть представлены формулой, геометрической фигурой, таблицей, графом, многочленом, матрицей и.т.д.
Представление
кода числа А в виде многочлена для любой
позиционной системы счисления есть
сумма произведений коэффициента аi
и веса xi
i-го разряда кода:
 .
.
В
качестве коэффициента
 используют целое неотрицательное число,
причем
используют целое неотрицательное число,
причем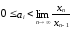 ,где
,где - основание системы счисления.
- основание системы счисления.
Представление кода в виде геометрической модели возможно благодаря тому, что кодовые комбинации n-значного кода могут рассматриваться как определенные точки n-мерного пространства. Так, геометрическая модель двузначного кода представляет собой квадрат - фигуру двумерного пространства; трехзначного - куб (фигуру трехмерного пространства).
