Министерство образования Российской Федерации

Сибирский государственный аэрокосмический университет имени академика М.Ф. Решетнева.

Курсовой проект

по дисциплине: Цифровые системы управления и обработки информации.

"Анализ и синтез цифровой системы управления с заданной передаточной функцией непрерывной её части"

Вариант 10б

Выполнила студентка группы ИУТ-01

Конохова Ю.Е.

Проверил доцент каф. ИУС

Серегин Ю.Н.

Красноярск 2012

Содержание

Исходные данные и задание на курсовой проект

Дан объект управления, представленный в виде логарифмической амплитудной характеристики и следующими показателями:

k=120 – коэффициент усиления

w_C=444с-1 – частота среза

Вид логарифмической амплитудной характеристики представлен на рисунке 1.

Рис. 1. ЛЧХ исходного объекта регулирования

Структурная схема исходного объекта регулирования изображена на рисунке 2.

Рис.2. Структурная схема объекта регулирования

Задание

• Получить исходную передаточную функцию объекта регулирования

• Представить исходный объект регулирования в виде ЦСУ и провести его анализ

• Определить передаточную функцию ЦСУ, отвечающую показателям качества

• Проверить показатели качества синтезированной ЦСУ

• Вычислить разностное уравнение корректирующей системы

• Построить блок-схему алгоритма вычисления разностного уравнения коррекции

Определение передаточной функции и параметров непрерывной части системы

Общий вид передаточной функции для данной схемы

(1)

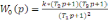
Моей задачей стояло подобрать коэффициенты Т₁,Т₂, Т₃ из формулы (1)

Коэффициенты Т₁ и Т₂ находятся левее частоты среза, но Т_3, правее. Значит, первые две точки надо подобрать так, чтобы они были больше 1/444, а третья находилась в промежутке между 1/444 и периодом дискретности 1/(2.5*444).

Т1=0.05 с. Т2=0.003 с. T3=0.001 с.

Период дискретности T= 0.0009 с.

Построим ЛАХ и ФЧХ исходной передаточной функции (рис 3).

Рис. 3. ЛАХ и ФЧХ исходной передаточной функции

Уравнение разомкнутой системы

(2)

Представление передаточной функции разомкнутой и замкнутой системы управления в z-форме.

Исходную непрерывную систему преобразуем к цифровому виду, для этого в структурную схему вводим дискретный элемент, который в общем виде можно представить в виде экстраполятора 0 порядка с передаточной фунцией:

Тогда структурная схема приобретет вид, представленный на рисунке 4.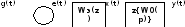

Рис.4. Структурная схема объекта регулирования с экстраполятором 0 порядка

Передаточную функцию разомкнутой системы можно представить в виде:

(3)

(4)

Z-изображение формулы (3) имеет вид:

Чтобы оценить устойчивость необходимо перейти к замкнутой системе. Общий вид формулы замкнутой системы:

Используя выше представленную формулу, получили уравнение замкнутой системы:

(5)

Для того чтобы найти корни замкнутой системы необходимо знаменатель уравнения (5) приравнять к 0. В результате получаем следующие значения:

Z1= 1.1430

Z2=0.7684

Исходя из критерия устойчивости, так как корни выходят за окружность единичного радиуса - система не устойчива.

Преобразование дискретной передаточной функции относительно псевдо частоты

Чтобы использовать частотный метод для синтеза дискретную передаточную функцию преобразуем относительно псевдо частоты. После преобразования получим передаточную функцию:

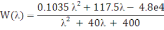
(6)

Построим неизменяемую ЛАХ на псевдо частоте (рис.5).

Рис. 5. ЛАХ и ФЧХ неизменяемой части системы на псевдо частоте

Для того чтобы сделать систему устойчивой избавимся от звена 2 порядка, разделив его на 2 апериодических звена. Желаемая передаточная функция примет вид.

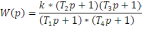
(7)

Для желаемой системы вычислим передаточную функцию в z-форме.

(8)

Из формулы (8) получаем уравнение скорректированной передаточной функции на псевдо частоте.

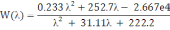
(9)

Построим ЖЛАХ и ЖФЧХ и ЛАХ и ФЧХ на псевдо частоте (рис.6).

Рис. 6. ЖЛАХ и ЖФЧХ и неизменяемые ЛАХ и ФЧХ.

Оценка устойчивости жлах

Для оценки устойчивости синтезированной системы необходимо привести ее к замкнутому виду.

(10)

Приравняем знаменатель уравнения (10) к нулю и найдем корни синтезированной системы.

Z1= 0.8890 + 0.0708i

Z2= 0.8890 - 0.0708i

Исходя из критерия устойчивости, так как корни находятся внутри окружности единичного радиуса, значит система устойчива.

Построение переходного процесса и определение показателей качества.

Построим переходной процесс синтезированной системы для оценки качества.

Используем единичное воздействие H(z)=F_скорр (z)*Z{1(t)}

Рис. 7. Переходной процесс синтезированной системы

Используя график переходного процесса синтезированной системы можно определить следующие динамические характеристики:

t_пп=0,032 с. - время переходного процесса.

=1/(2.5*444)=0,0009 с. – период дискретности;

T_пп=0.032/ 0.0009 - время регулирования 35 тактов.

σ= 16,7% - перерегулирование.

Из показателей качества переходного процесса (рис. 7) следует, что спроектированная цифровая система управления соответствует показателям качества, предъявляемым к техническим системам.