Основы механики твердого деформируемого тела

Что же касается степени статической неопределимости конструкции, для которой C >3K, но rA <3K, то она вычисляется по формуле

совпадающей при rA = 3K с формулой (1.9).

Теперь о матрице D. Приведенная после записи физического закона (1.7) структура этой матрицы отвечает случаю, когда все стержни конструкции, включая опорные, имеют конечную осевую жесткость. Между тем жесткости некоторых стержней (и прежде всего опорных) могут быть столь большими, что такие стержни приходится рассматривать как абсолютно жесткие. Для них закон Гука записан быть не может, поэтому из соотношений (1.7) изымается столько уравнений, сколько в конструкции имеется нерастяжимых стержней. Вместо убранных уравнений добавляется столько же соотношений вида ∆i = 0, свидетельствующих о недеформируемости абсолютно жестких элементов. Таким образом, баланс между числом неизвестных и числом уравнений задачи сохраняется, хотя структура полной системы уравнений конструкции изменится.

И последнее. Полученные выше результаты справедливы лишь для конструкции, стержни которой выполнены из материала, подчиняющегося закону Гука, и перемещения узлов которой малы. Такая конструкция называется линейно деформируемой. Никакие другие конструкции в настоящем разделе пособия не рассматриваются.

1.5. Учет временной нагрузки. На рис.1.2 изображена плоская конструкция, загруженная по верхнему поясу постоянно действующими силами Pk и временно прикладываемыми силами Tk, k = 1, 2, . . . , 5. Величины сил Tk известны, но сколько из них одновременно действуют на конструкцию и в каких именно узлах, заранее не определено. Можно ожидать приложения сил Tk в любых сочетаниях. Интерес представ-

ляют такие комбинации воздействий Pk и Tk, которые порождают в стержнях наибольшие по модулю усилия. Такие усилия называют расчетными. Задача отыскания расчетных усилий может быть решена следующим образом. Ферма рассчитывается на фиксированные положения узловых сил 1 + KT раз, где KT – число узлов фермы, в которых могут действовать силы Tk (в примере на рис. 1.2 KT = 5). Один из расче-

тов выполняется на постоянную нагрузку, а все остальные – на поочередное действие сил T1, T2 и т. д. Для вычислений может использоваться формула (1.11a), но только теперь как матрица P заданной нагрузки, так и

искомая матрица N усилий будут иметь по 1+KT столбцов. В строке с номером i матрицы N содержатся значения Ni(0), Ni(1), . . . , Ni(KT) продольной силы N в i-м стержне от постоянной нагрузки и сил T1, T2 и т. д. соответственно. Некоторые из сил Tk приведут к растяжению данного стержня, другие – к его сжатию. Пусть Ni+ – усилие, возникающее в стержне с номером i от одновременного действия только тех сил Tk, которые его растягивают. Одновременное действие всех остальных сил Tk вызовет в рассматриваемом стержне отрицательное усилие Ni−. Постоянная нагрузка находится на конструкции всегда, и как бы ни были приложены силы Tk, суммарное усилие в стержне i не выйдет за пределы

Если эти величины имеют один знак, то в качестве расчетного усилия Ni берется большая´ из них по модулю. В противном случае при оценке прочности стержня используются обе границы (1.14) для усилия Ni. Здесь нужно учитывать как материал стержня (хрупкий или пластичный), так и возможность его выпучивания при сжатии.

В основу описанного расчета конструкции был заложен принцип наложения. Можно пойти по пути использования этого принципа дальше. Схема вычислений такова. К узлам фермы последовательно прикладываются силы T1 = 1, T2 = 1 и т. д., на которые и выполняется расчет по формуле (1.11a). Полученную в результате расчета матрицу N, насчитывающую KT столбцов, называют матрицей влияния. По каждой ее строке можно проследить, как сказывается на соответствующем усилии переход единичной силы из одного загружаемого узла в другой. Искомые усилия Ni(1), Ni(2), . . . отличаются от единичных усилий Ni(1), Ni(2), . . . лишь множителями T1, T2, ....

Матрица влияния используется для определения усилий от постоянной нагрузки:

Ni(0) = Ni(1) · P1 + . . . + Ni(KT) · PKT ,

атакже для расчета на любое временное воздействие на конструкцию.

Внастоящей главе не было приведено примеров, доведенных до числа. Это и понятно: слишком велик объем данных, которыми приходится оперировать при вычислениях по формулам типа (1.11a). Громоздкие вычислительные упражнения мало способствуют пониманию особенностей поведения конструкции под нагрузкой. В этом отношении больший´ интерес представляют те подходы к расчету стержневых конструкций, о которых рассказывается в главах 3–7. Но именно после прочтения этой главы становится ясным, насколько важно для специалиста в области строительной механики владение методами вычислительной математики и, в частности, численными методами алгебры.

ГЛАВА 2. ИЗГИБАЕМЫЕ СТЕРЖНЕВЫЕ КОНСТРУКЦИИ

2.1. Полная система уравнений изгибаемой конструкции. Ниже рассматриваются стержневые конструкции, элементы которых испытывают не только осевую деформацию. Сюда относятся балки, рамы, арки, пространственные каркасы сооружений, различные комбинированные системы. При прочностном расчете таких конструкций требуется, как и при расчете ферм, находить усилия и перемещения от заданного воздействия, определять кинематический тип сооружения, отыскивать опасные положения временных нагрузок. Все эти задачи могут быть решены с помощью полной системы уравнений, описывающей состояние конструкции. Для пространственной конструкции эта система громоздка, что связано и с большой размерностью задачи, и с многообразием конструктивных решений узлов: сферические шарниры, цилиндрические шарниры и т. п. А между тем отличия в построении полной системы уравнений для шарнирно-стержневой и произвольной стержневой конструкций видны уже на примере плоской конструкции, состоящей из призматических элементов. Именно плоская стержневая конструкция, да еще при условии, что на ее перемещения не влияет деформация сдвига, и рассматривается в настоящей главе.

По торцам стержня i, выделенного из плоской конструкции, действуют шесть усилий (рис. 2.1). Это усилия Mik, Qik, Nik, отнесенные к началу k стержня, и усилия Mij, Qij, Nij, прикладываемые к его концу j (k < j). Усилия, изображенные на рис. 2.1, считаются положительными. Независимыми являются только три

из них: выделенный стержень находится в состоянии покоя и три условия равновесия этого стержня связывают величины Mik, Qik, Nik, Mij, Qij, Nij между собою. В качестве независимых статических параметров состояния стержня здесь принимаются изгибающие моменты Mik и Mij и продольная сила Nik в его начале. Другой выбор независимых усилий приведет к несколько иной форме полной системы уравнений. Из условий равновесия стержня следует, что

Nij = Nik + Ni(P ), Qik = −(Mik + Mij)/Li + Qk(P ),

Qij = −(Mik + Mij)/Li + Qj(P ),

где Ni(P ), Qk(P ), Qj(P ) – слагаемые, определяемые пролетной нагрузкой на стержень. Если таковая отсутствует, то

На рис. 2.2 показан отделенный от конструкции узел с приложенными к нему внешними силами Xk, Yk и моментом Mk, а также усилиями, заменяющими действие отброшенных стержней. Чтобы не загромождать чертеж, усилия изображены лишь в одном из разрезов. При записи условий равновесия ΣX = 0, ΣY = 0, ΣMk = 0 рассматриваемого узла, помимо введенных в

п. 1.2 обобщенных направляющих косинусов lki и mki, потребуется еще одно вспомогательное понятие. Речь идет о символе инцидентности δki, который принимается равным единице: δki = 1, если стержень i подходит к узлу с номером k, и нулю: δki =0, если стержень i и узел k не инцидентны.

Тогда

C

P

(lkiNik + mkiQik) + Xk = 0,

i=1

C

P(mkiNik − lkiQik) + Yk = 0, i=1

C

P δkiMik + Mk = 0, i=1

где C – полное число стержней конструкции. Из приведенных уравнений надо при помощи формул типа (2.1) исключить все поперечные и продольные силы в торцах, где стержни заканчиваются, а затем объединить получившиеся соотношения для всех K неопорных узлов конструкции. В результате получится система уравнений равновесия конструкции вида

Здесь A – матрица, элементами которой являются обобщенные направляющие косинусы, символы инциденции, а также (из-за использования формул (2.1)) длины стержней. Эта матрица имеет 3K строк и 3C столбцов. Вектор S содержит искомые торцевые усилия:

Он насчитывает 3C элементов. Столбец P узловой нагрузки состоит из 3K элементов. Он также имеет блочную структуру:

При наличии пролетных нагрузок к узловым силам Xk и Yk добавляются слагаемые, связанные с использованием формул, порождающих соотношения (2.1).

Условия равновесия (2.2) составлены для конструкции с жесткими узлами. Если же имеются не только жесткие узлы, надо составить дополнительные условия равновесия, учитывающие характер прикрепления стержня. Так, если стержень i крепится к узлу k при помощи шарнира, фиксируется равенство нулю торцевого изгибающего момента Mik : Mik = 0. Аналогично может быть учтено и любое иное нежесткое присоединение стержня к узлу (см. далее пример расчета плоской рамы в п. 4.1). Пусть всего составлено d дополнительных уравнений равновесия конструкции и пусть все они присоединены к системе (2.2). Матрица A преобразованной системы статических уравнений будет иметь 3K+d строк. Такое же число элементов содержит и вектор P заданной нагрузки.

Чтобы получить физические и кинематические уравнения задачи, надо ввести кинематические параметры состояния. Ясно, что их надо выбрать сопряженными по работе с независимыми торцевыми усилиями стержней и узловыми нагрузками. Для этого в качестве интегральных деформаций стержня берется

его удлинение i, а также повороты ϕik и ϕij его торцов. На рис. 2.3 изображен стержень, у которого все другие перемещения концов, кроме только что названных, отсутствуют. Связь между величинами i, ϕik, ϕij и усилиями Nik, Mik, Mij дают закон Гука (1.7) и формула Мора (II.9.18c). При дальнейших вычислениях используется правило (II.6.11a) перемножения эпюр, для чего и нужны эпюры изгибающих моментов, приведенные на рис. 2.3. Итак,

– матрица податливости стержня i и вектор его интегральных деформаций. Тогда

где εPi – слагаемое, учитывающее пролетную нагрузку, если таковая имеется. Элементы вектора εPi также могут быть найдены при помощи формулы (II.9.18c). Объединение равенств (2.3a) для всех C стержней приводит к физическим уравнениям конструкции:

Матрица F представляет собой матрицу податливости плоской изгибаемой конструкции.

Чтобы получить кинематические уравнения конструкции, опираясь на принцип двойственности, надо ввести перемещения uk, vk, θk, сопряженные с узловой нагрузкой. Первые два из них суть линейные перемещения узла k вдоль осей 0x и 0y, последнее – поворот по направлению сосредоточенного момента Mk. Из 3K перемещений всех узлов составляется вектор

h i h i

V > = V1>...Vk>...VK> , Vk> = uk vk θk .

Наконец, по аналогии с формулой (2.2) записывается равенство

Совокупность соотношений (2.2), (2.4), (2.5) и образует полную систему уравнений плоской конструкции, состоящей из призматических стержней.

2.2. О двух подходах при расчете стержневых конструкций. Систему уравнений (2.2), (2.4), (2.5) можно исследовать точно так же, как исследовалась полная система уравнений шарнирно-стержневой конструкции. Да и выводы из этих исследований будут аналогичными. Так, если матрица A уравнений равновесия (2.2) квадратная и невырожденная, то конструкция является статически определимой и неизменяемой. При отсутствии нагрузки вектор P является нулевым и уравнения (2.2) имеют единственное решение S = 0. Значит, и в изгибаемой статически определимой конструкции усилия могут возникнуть только при силовом воздействии. Если матрица A прямоугольная с числом столбцов, превышающим количество строк, то конструкция имеет избыточные связи и является статически неопределимой. Она будет неизменяемой тогда и только тогда, когда ранг матрицы A максимален. Рассчитывая статически неопределимую конструкцию, надо от полной системы уравнений переходить к разрешающим уравнениям в перемещениях или усилиях по схеме, описанной в п. 1.4. Повторять все сказанное там еще раз нет необходимости.

Описанный подход к решению задачи строительной механики можно квалифицировать как весьма формальный. Он удобен тем, что сводится к выполнению ясных вычислительных операций, но даже при сравнительно небольших числах C и K приходится иметь дело с внушительными по объемам массивами. Поэтому о наглядности результатов, получаемых на различных этапах расчета, говорить не приходится. Нет такой конструкции, в которой можно было бы оперативно найти усилия или установить ее кинематический тип при помощи полной системы уравнений. Вот почему необходимо познакомиться и с иными методами решения задачи. Эти методы основаны на анализе структуры конструкции, представляемой в ходе исследования в виде набора гораздо более крупных единиц (так называемых дисков), нежели отдельные стержни. Правила выделения подконструкций (дисков), особенности взаимодействия между отдельными дисками, их внутреннее состояние и являются предметом изучения при описанном подходе к решению задачи. Только таким образом можно прийти к пониманию работы силовых конструкций. Владеть качественными методами исследования их напряженно-деформированного состояния полезно любому инженеру, имеющему дело с прочностными расчетами, тогда как формальные методы расчета нужно глубоко знать лишь узким специалистам в области строительной механики. Вот почему в настоящем курсе формализированным алгоритмам вычислений отводится не так уж много места.

2.3. Диски и связи. Правила соединения дисков. Диском называют любую неизменяемую часть плоской стержневой конструкции. В роли диска может выступать либо отдельный стержень с любым очертанием оси

(рис. 2.4a), либо набор стержней, связанных друг с другом так, что взаимные жесткие смещения между элементами набора отсутствуют. Иначе говоря, расстояние между двумя любыми точками на диске может измениться только в результате деформирования этого диска. Очевидна, например, неизменяемость группы стержней, изображенных на рис. 2.4b, ибо трем отрезкам заданной длины отвечает единственная конфигурация треугольника. Набор любого числа треугольников также образует диск (рис. 2.4c). На рис. 2.4d показано условное изображение диска.

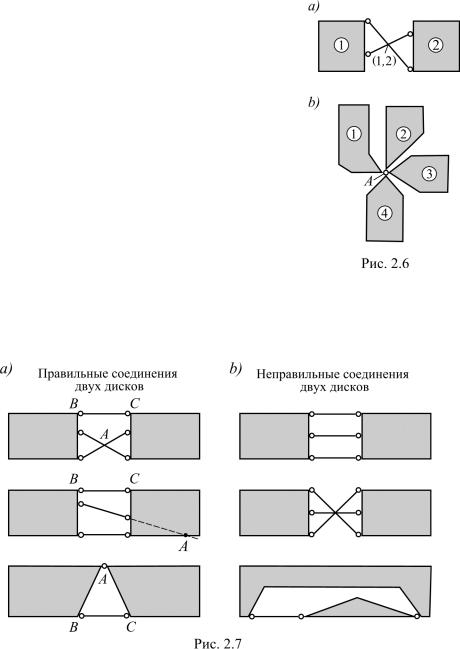
Незакрепленный диск обладает тремя степенями свободы. Для ограничения его перемещений используются различные соединительные устройства. Устройство, при помощи которого может быть ликвидирована одна степень свободы, называют связью. Если какое-либо устройство позволяет устранить n степеней свободы, то оно рассматривается как n связей. К устройствам, ограничивающим подвижность диска, относятся стержень, шарнир и заделка (защемление). Стержень (рис. 2.5a) ликвидирует одну степень свободы между дисками (т. е. является связью), препятствуя их взаимному перемещению вдоль своей оси. На попытку осуществить такое перемещение стержень ответит возникающей в нем реакцией R. Шарнир ограничивает любые взаимные линейные перемещения дисков, между которыми он поставлен. Это устройство ликвидирует две степени свободы. В шарнире может возникнуть реакция R любого направления, которую удобства ради раскладывают по двум наперед заданным направлениям (рис. 2.5b). Шарнир эквивалентен двум стержням. Два стержня, поставленные между двумя дисками, можно заменить шарниром, расположенным в точке пересечения стержней. На рис. 2.6a эта точка, играющая роль относительного мгновенного центра вращения дисков, обозначена через (1, 2).

Шарнир, связывающий D дисков, называют сложным, или кратным, шарниром. Сложный шарнир A, изображенный на рис. 2.6b, эквивалентен трем обычным шарнирам. Он используется как устройство, соединяющее диски 1 и 2, затем как устройство, присоединяющее к дискам 1 и 2 диск 3, и, наконец, как устройство, добавляющее к указанным дискам диск с номером 4. Таким образом,

сложный шарнир, поставленный между D дисками, кратен D−1 простому шарниру.

Защемление (рис. 2.5c) препятствует любым взаимным смещениям дисков, ликвидируя все три степени свободы между ними. В нем могут возникнуть реактивный момент и реактивная сила, которую удобства ради раскладывают по двум заданным направлениям. Так как диски, между которыми расположена заделка, можно объединить в один более крупный диск, это устройство при исследовании структуры сооружения рассматриваться не будет.

Связи, поставленные между дисками и землей, относятся к опорным.

Соединение дисков называют правильным, если оно приводит к неизменяемой системе. Правильное соединение двух дисков обеспечивается постановкой между ними трех стержней, не пересекающихся в одной точке, или шарнира и стержня, если только шарнир не находится на той же прямой,

что и ось стержня. В указанных случаях вновь образованная система имеет очертание треугольника, из чего и следует сформулированное выше утверждение. Примеры правильных и неправильных соединений двух дисков приведены соответственно на рис. 2.7a и b.

Последовательно применяя правило соединения двух дисков, можно получить неизменяемую систему из любого их числа. Но для правильного соединения трех дисков друг с другом имеется еще одна возможность. Три диска можно объединить в неизменяемую систему при помощи трех шар-

ниров, связывающих диски попарно, если только шарниры не находятся на одной прямой (конфигурация треугольника). На рис. 2.8a приведены примеры такого соединения. На рис. 2.8b показано, как три диска неверно соединены друг с другом.

Получить неизменяемую систему из D дисков можно не только так, как об этом было сказано выше. Но лишь образованные по правилам соединения двух или трех дисков конструкции называют конструкциями простой структуры, или простыми конструкциями.

2.4.Мгновенно изменяемые конструкции. Согласно сказанному в

п.2.3, системы, изображенные на рис. 2.9a,b, изменяемы. Но если сообщение о подвижности первой из них воспринимается как само собой разумеющееся: ничто не мешает одному диску переместиться без деформирования материала относительно другого на конечное расстояние v, то аналогичное утверждение по поводу второй конструкции может показаться сомнительным. И