
Архив2 / курсовая docx200 / Kursovaya_rabota(5)
.docxБалтийский Государственный Технический Университет
«ВОЕНМЕХ» им. Д.Ф. Устинова
Кафедра И4
Курсовая работа
по дисциплине «Радиотехнические цепи и сигналы»
вариант 11-5
Выполнил: Певзнер Д.Я. гр. И491
Проверил: Свешников О.В.
Санкт-Петербург
2011
Оглавление
Задание на курсовую работу 2
1. Теоретическая часть 3
1.1. Расчет спектральной плотности, амплитудного и фазового спектров сигнала и его автокорреляционной функции 3
1.2. Расчет передаточной, амплитудно-частотной, фазо-частотной и импульсной характеристик заданной RC-цепи.. 5
1.3. Расчеты сигнала и его спектра на выходе заданной RC-цепи при подаче на ее вход заданного сигнала.. 8
2. Результаты компьютерного моделирования 9
Заключение 10
Список использованной литературы 11
Приложение 1. Результаты компьютерных расчетов 12
Задание на курсовую работу
Вариант 11-5
Входное воздействие:
|
|
|
|
|
|
|
|
5 |
2 |
8 |
2 |
2 |
1 |

Линейная RC-цепь:
|
|
|
|
|
|
|
|
1 |
0,05 |
0 |
0,1 |
250 |
2000 |

Теоретическая часть должна включать:
-
расчеты спектральной плотности, амплитудного и фазового спектров сигнала и его автокорреляционной функции;
-
расчеты передаточной, амплитудно-частотной, фазо-частотной и импульсной характеристик заданной RС-цепи;
-
расчеты сигнала на выходе заданной RС-цепи при подаче на её вход заданного сигнала.
Также необходимо предоставить:
-
результаты компьютерных расчетов;
-
результаты компьютерного моделирования прохождения сигнала через линейную цепь.
1. Теоретическая часть
1.1 . Расчет спектральной плотности, амплитудного и фазового спектров сигнала и его автокорреляционной функции.
Заданный сигнал можно представить в виде:

Используя
единичную функцию
 выражение можно представить в виде:
выражение можно представить в виде:

График заданного сигнала представлен на рис. 1.

Рис. 1. График исходного сигнала
Спектральная
плотность сигнала находится подстановкой
выражения
 ,
описывающего заданный сигнал, в прямое
преобразование Фурье и вычислением
интеграла:
,
описывающего заданный сигнал, в прямое
преобразование Фурье и вычислением
интеграла:

Для
заданного сигнала интеграл нужно
вычислять на промежутке, равном периоду
сигнала
 .
Таким образом, получаем:
.
Таким образом, получаем:

=![]()
Сделаем
замену
 в получившейся функции. Амплитудный
спектр сигнала (рис. 2) равен модулю
спектральной плотности:
в получившейся функции. Амплитудный
спектр сигнала (рис. 2) равен модулю
спектральной плотности:
 .
Фазовый спектр сигнала (рис. 3) равен
аргументу спектральной плотности:
.
Фазовый спектр сигнала (рис. 3) равен
аргументу спектральной плотности:
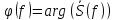 .
.

Рис. 2. Амплитудный спектр сигнала

Рис. 3. Фазовый спектр сигнала
Автокорреляционная функция сигнала определяется по формуле:

Данная
функция является временной характеристикой
сигнала, определяющей степень связи
среднего значения сигнала
 со значениями его копии
со значениями его копии
 сдвинутой на время
сдвинутой на время
 .
.
Для заданного сигнала интеграл выглядит следующим образом:

График полученной автокорреляционной функции представлен на рис. 4

Рис. 4. Автокорреляционная функция сигнала
При
 получается максимальное значение
функции, оно численно равно энергии
сигнала:
получается максимальное значение
функции, оно численно равно энергии
сигнала:
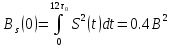
1.2. Расчет передаточной, амплитудно-частотной, фазо-частотной и импульсной характеристик заданной RC-цепи.
Рассмотрим заданную RC-цепь (рис. 5).
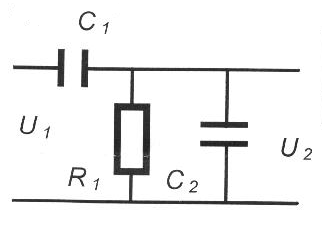
Рис. 5. Исходная RC-цепь
Коэффициент передачи цепи в операторной форме находится по формуле:




Подставим в коэффициент передачи значения С1=100 пФ, С2=200 пФ, R1=250 кОм:

Передаточная
характеристика определяется из
коэффициента передачи путем подстановки
 :
:

Сделаем
замену
 в получившейся функции. Амплитудно-частотная
характеристика заданной цепи (рис. 6)
равна модулю передаточной функции:
в получившейся функции. Амплитудно-частотная
характеристика заданной цепи (рис. 6)
равна модулю передаточной функции:
 .
Фазово-частотная характеристика (рис.
7) равна аргументу передаточной функции:
.
Фазово-частотная характеристика (рис.
7) равна аргументу передаточной функции:
 .
.

Рис. 6. Амплитудно-частотная характеристика цепи

Рис. 7. Фазо-частотная характеристика цепи
Рассчитаем
импульсную характеристику цепи
 ,
выполнив обратное преобразование
Лапласа от коэффициента передачи H(p).
С этой целью найдем полюсы H(p),
соответствующие корням уравнения 3p
+ 40000. Корень этого уравнения p1
= -13333 является простым. По теореме
разложения, получается формула для
импульсной характеристики:
,
выполнив обратное преобразование
Лапласа от коэффициента передачи H(p).
С этой целью найдем полюсы H(p),
соответствующие корням уравнения 3p
+ 40000. Корень этого уравнения p1
= -13333 является простым. По теореме
разложения, получается формула для
импульсной характеристики:

После подстановки p1 окончательно получаем:

График импульсной характеристики цепи представлен на рис. 8.

Рис. 8. Импульсная характеристика цепи
1.3. Расчеты сигнала и его спектра на выходе заданной RC-цепи при подаче на ее вход заданного сигнала
Сигнал
на выходе линейной стационарной цепи
может быть найден двумя способами:
временным и частотным. Рассмотрим
временной метод анализ линейной цепи,
он основан на использовании импульсной
характеристики цепи. Если параметры
линейной цепи не изменяются во времени
(т.е. линейная цепь является стационарной),
то выходная реакция цепи на произвольное
входное воздействие определяется
сверткой входного воздействия
 с импульсной характеристикой цепи
с импульсной характеристикой цепи


Результат представлен на риc. 9:

Рис. 9. Рассчитанный выходной сигнал
2. Результаты компьютерного моделирования
Чтобы смоделировать прохождение сигнала через заданную RC-цепь, воспользуемся программой для моделирования и анализа работы электрических цепей NI Multisimтм 11.0 (рис. 10):

Рис. 10. Вид цепи в Multisimтм 11.0
Используя настраиваемый генератор напряжения, можно задать входной сигнал, подать его на вход цепи и с помощью осциллографа увидеть сигнал на выходе (рис. 11). Масштаб по оси времени – 2 мс, по оси напряжения – 100 мВ.

Рис. 11. Смоделированный выходной сигнал
Сравнив рассчитанный выходной сигнал (рис. 9) и смоделированный (рис. 11), можно сделать вывод ,что они идентичные. Следовательно, расчёт произведен верно.
Заключение
В процессе работы были получены основные знания по анализу сигналов в радиотехнических цепях (определение амплитудного и фазового спектров, расчёт спектральной плотности), а также навыки исследования несложных линейных цепей(определение АЧХ, ФЧХ, импульсной характеристики). Также приобретён опыт работы с двумя компьютерными САПР: Mathcad 14.0 и Multisim 11.0. Mathcad позволяет в короткие сроки выполнить сложные расчёты, получить выходные данные и наглядно отобразить результат. Multisim 11 отлично подходит для моделирования и анализа электрических схем, позволяет увидеть работу эл. цепи, не создавая её реальный физический аналог. Объём необходимых знаний по предмету «РТЦиС» не исчерпывается данной курсовой работой, изучение новых тем будет продолжено.
Список использованной литературы
1. РТЦ и С. Методические указания по выполнению курсовой работы. Л. Б. Кочин, В. К. Соколов. СПб, 2002;
2. РТЦ и С. С. И. Баскаков. Москва, 2003.
3. РТЦ и С. И. С. Гоноровский. Москва, 1986.
Приложение 1. Результаты компьютерных расчётов




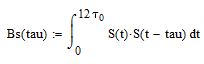













 ,
В
,
В , мс
, мс



 ,
кОм
,
кОм , пФ
, пФ