Архив2 / курсовая docx200 / Kursovaya_po_vychmatu

Балтийский государственный технический университет

«ВОЕНМЕХ» им. Д. Ф. Устинова

Курсовая работа

По дисциплине «Вычислительная математика»

Вариант 12

Приняла: Мартынова Татьяна Евгеньевна

Санкт-Петербург.

2012 г.

Лабораторная работа №1

«Определение абсолютной и относительной погрешностей приближенных чисел» Оценка погрешностей результата

Задание №1

Подъемная сила крыла самолета оценивается по формуле F= cS, где S- площадь проекции крыла на горизонтальную плоскость, - скорость натекания воздуха на крыло, - плотность атмосферы на данной высоте, - угол атаки, отсчитываемый от направления нулевой подъемной силы, с – коэффициент, зависящий от формы крыла. Требуется вычислить F и при заданных значениях с, , , , S и заданных абсолютных и относительных значениях этих величин.

Вариант№12

Решение:

Ответ: _.

Задание №2

Найти абсолютную погрешность вычисления функции

при заданных значениях аргументов.

Решение:

	1	2	3
	0.2850.0002	0.27310.0002	5.8430.001
	0.640.004	10.80.02	4.170.001

Лабораторная работа №2

«Интерполирование и экстраполирование данных. Интерполяционный многочлен Лагранжа»

Задание №1

Восстановить интерполяционный многочлен Лагранжа

Вариант № 12

Решение:

Задание №2

Используя схему Эйткена, вычислить приближенное значение функции , заданной таблично при данном аргументе x_t.

Решение:

++

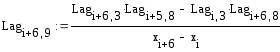
Лабораторная работа №3

«Интерполирование и экстраполирование данных. Интерполяционный многочлен Ньютона»

Задание №1

Вариант 12

Найти приближенное значение функции y=f(x) при данном значении аргумента xt с помощью интерполяционного многочлена Ньютона, если функция задана в неравноотстоящих узлах таблицы и xt=0.291

Решение:

Ответ:

Лабораторная работа №4

«Аппроксимация функции по методу наименьших квадратов»

Задание №1

Вариант 12

По методу наименьших квадратов аппроксимировать таблично заданную функцию y=f(x) многочленом наилучшего среднеквадратического приближения (1≤m≤4)

Решение:

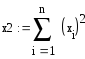
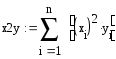
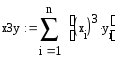
Лабораторная работа № 8

«Численное дифференцирование и численное интегрирование функций»

Задание №1

Вариант 12

Для данных функций построить правую, левую и центральную первые разностные производные, вторую разностную производную на указанном интервале с данными шагами сетки h₁ и h₂ и сравнить полученные значения с точными значениями производных: