
- •2013 Год
- •Правило знаков для продольной силы n.
- •Диаграмма растяжения низкоуглеродистой стали
- •Последовательность выполнения расчета на прочность при растяжении или сжатии.
- •Практическая работа № 6 «Построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии»
- •Практическая работа №7 «Расчеты на прочность при растяжении и сжатии».
- •Лабораторная работа №2 «Испытание на растяжение образца из низкоуглеродистой стали».
- •Порядок выполнения и оформления работы
- •Расчетно-графическая работа №5 «Построение эпюр продольных сил и нормальных напряжений при растяжении и сжатии»
- •Расчетно-графическая работа №6 «Определение коэффициента запаса прочности при растяжении и сжатии».
Правило знаков для продольной силы n.
Если внешняя сила F направлена от сечения, то сила N –положительная, если внешняя сила F направлена к сечения, то сила N –отрицательная.
При решении задач, силу N будем считать положительной, и направлять её от сечения. Если при решении задачи, сила N будет отрицательной, это означает, что она направлена к сечении.
Если продольная сила направлена от сечения, то брус растянут. Растяжение считается положительной деформацией.
Если продольная сила направлена к сечения, то брус сжат. Сжатие считается отрицательной деформацией.
Изменение продольный силы по длине бруса удобно представлять в виде диаграммы, называемой эпюрой продольных сил.
Ось эпюры параллельна продольной силе. Нулевая линия проводится тонкой линией. Значения сил откладываются от оси, вверх – положительные, вниз – отрицательные. В пределах одного участка значение силы не меняется, поэтому эпюра очерчивается отрезками прямых линий, параллельными оси Oz.
Эпюра
штрихуется тонкими линиями, перпендикулярными
оси. Для наглядности на эпюрах N
и
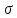 знаками
« + » и « —» отмечаются положительные и
отрицательные значения участков эпюр.
знаками
« + » и « —» отмечаются положительные и
отрицательные значения участков эпюр.
При
растяжении и сжатии в поперечных сечениях
бруса возникают только нормальные
напряжения, равномерно распределенные
по сечению
и вычисляемые по формуле
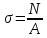 ,
,
где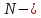 продольная сила;A-
площадь поперечного сечения. Очевидно,
что при растяжении и сжатии форма сечения
на напряжение не влияет.
продольная сила;A-
площадь поперечного сечения. Очевидно,
что при растяжении и сжатии форма сечения
на напряжение не влияет.
Во всех сечениях бруса напряжения распределены равномерно и что в сечении, где к брусу приложена вдоль оси сосредоточенная сила, значения продольной силы и напряжений меняются скачкообразно.
Пример. Построить эпюры продольных сил и нормальных напряжений для ступенчатого бруса .
Решение.
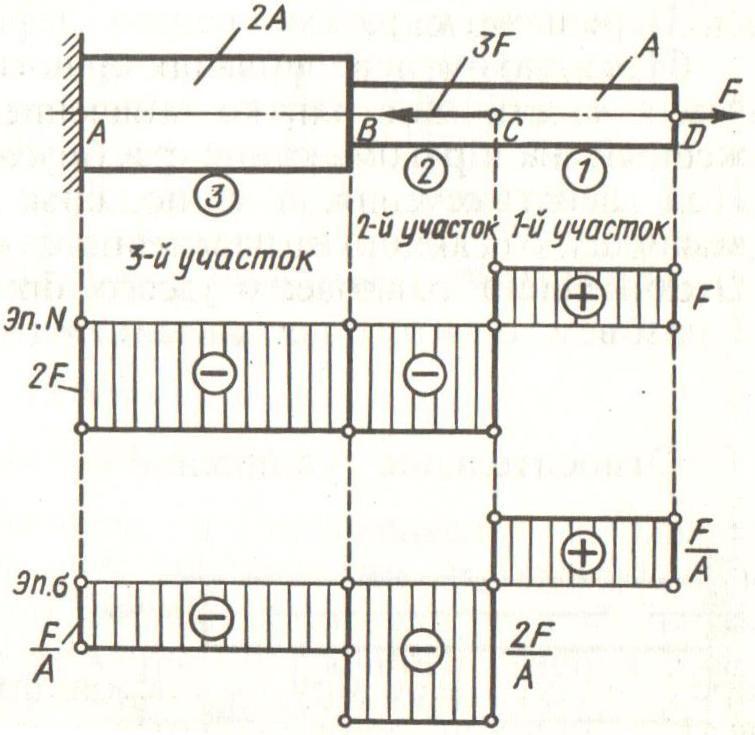
Разобьем брус на участки и пронумеруем их, как показано на рисунке.
Для построения эпюры продольных сил N под рисунком бруса проводим ось эпюры, параллельную оси бруса, и линиями ограничиваем его участки.
Приступим к построению эпюры N. Применяя метод сечений, устанавливаем, что во всех поперечных сечениях первого участка действует продольная си
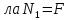 .
Откладываем вверх от оси эпюры величину
и произвольном масштабе и проводим
прямую, параллельную оси эпюры. В точке
С
бруса приложена
.
Откладываем вверх от оси эпюры величину
и произвольном масштабе и проводим
прямую, параллельную оси эпюры. В точке
С
бруса приложена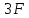 .
Применяя метод сечений, устанавливаем,
что во всех поперечных сечениях второго
и третьего участков действуем продольная
сил
.
Применяя метод сечений, устанавливаем,
что во всех поперечных сечениях второго
и третьего участков действуем продольная
сил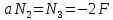 и эпюра N
будет горизонтальной линией, расположенной
на
и эпюра N
будет горизонтальной линией, расположенной
на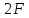 единиц ниже оси эпюры. Очевидно, что
значение ординаты эпюры продольных
сил под заделкой равно реакции заделки.
единиц ниже оси эпюры. Очевидно, что
значение ординаты эпюры продольных
сил под заделкой равно реакции заделки.Для построения эпюры
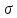 определим нормальные напряжения на
участках бруса, беряотношение
значения продольной силы (из опоры
определим нормальные напряжения на
участках бруса, беряотношение
значения продольной силы (из опоры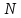 )
к площади поперечного сечения. Тогда
на первом участке нормальные напряжения
будут равны
)
к площади поперечного сечения. Тогда
на первом участке нормальные напряжения
будут равны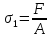 ,
на втором -
,
на втором -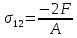 ,
на третьем -
,
на третьем -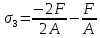 .
.Правила построения эпюры
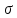 те же, что и для эпюрыN,
включая и правило знаков. В пределах
каждою из участков напряжения постоянны,
поэтому эпюра
те же, что и для эпюрыN,
включая и правило знаков. В пределах
каждою из участков напряжения постоянны,
поэтому эпюра
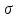 на каждом участке прямая, параллельная
оси.
на каждом участке прямая, параллельная
оси.
Перейдем к рассмотрению деформаций.
Представим
себе прямой брус постоянного поперечного
сечения А,
длиной
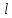 ,
жестко защемленный одним концом и
нагруженный на другом конце
растягивающей силой
,
жестко защемленный одним концом и
нагруженный на другом конце
растягивающей силой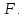 Под действием этой силы брус удлинится
на некоторую величину
Под действием этой силы брус удлинится
на некоторую величину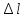 ,
которую назовемабсолютным
удлинением.
Отношение
абсолютного удлинения
,
которую назовемабсолютным
удлинением.
Отношение
абсолютного удлинения
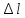 к первоначальной длине
к первоначальной длине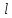 назовемотносительным
удлинением
и обозначим
назовемотносительным
удлинением
и обозначим
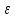 :
:
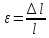

Относительное
удлинение
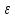 число отвлеченное, иногда его выражают
в процентах:
число отвлеченное, иногда его выражают
в процентах: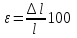
Итак, деформация бруса при растяжении и сжатии характеризуется абсолютным и относительным удлинением или укорочением.
Закон Гука при растяжении и сжатии
Напряжения и деформации при растяжении и сжатии связаны между собой зависимостью, которая называется законом Гука.
Закон Гука при растяжении и сжатии справедлив лишь в определенных пределах нагружения и формулируется так: нормальное напряжение прямо пропорционально относительному удлинению или укорочению.
Математически
закон Гука можно записан, в виде равенства:
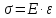
Коэффициент пропорциональности Е характеризует жесткость материала, т. е. его способность сопротивляться упругим деформациям растяжения или сжатия, и называется модулем продольной упругости или модулем упругости первого рода.
Модуль упругости и напряжение выражаются в одинаковых единицах:
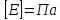 .
Значения Е, МПа, для некоторых материалов:
.
Значения Е, МПа, для некоторых материалов:
Чугун…..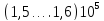 Сталь…...(1,96…2,16)
Сталь…...(1,96…2,16)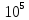
Медь
…..(1.0...1,3) К)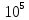 Сплавы алюминия …..(0,69…0,71)
Сплавы алюминия …..(0,69…0,71)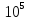
Дерево
(вдоль волокон) ………(0,1 ...0,16)
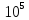
Если
в формулу закона Гука подставим выражения
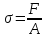 ,
,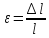
то
получим
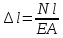 .Эта формула
называется формулой Гука.
.Эта формула
называется формулой Гука.
Произведение ЕА, стоящее в знаменателе, называется жесткостью сечения при растяжении и сжатии; оно характеризует одновременно физико-механические свойства материала и геометрические размеры поперечного сечения бруса.
Эта формула читается так: абсолютное удлинение или укорочение прямо пропорционально продольной силе, длине и обратно пропорционально жесткости сечения бруса.
Отношение
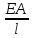 называетсяжесткостью
бруса при
растяжении или сжатии.
называетсяжесткостью
бруса при
растяжении или сжатии.
Для
бруса, имеющего несколько участков,
отличающихся материалом, размерами
поперечного сечения, продольной силой,
изменение длины всего бруса равно
алгебраической сумме удлинений и
укорочений отдельных участков:
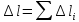 .
.
