§ 5.3. Корневые оценки качества

Корневыми оценками называются такие, которые ос­новываются на расположении корней характеристическо­го уравнения замкнутой системы, т. е. полюсов переда­точной функции замкнутой системы, а также и нулей этой передаточной функции.

Простейшей корневой оценкой качества является сте­пень устойчивости — расстояние η от мнимой оси до бли­жайшего корня на плоскости корней λ характеристиче­ского уравнения замкнутой системы (рис. 5.11). Если ближайшим является вещественный корень (рис. 5.11, а), то ему соответствует апериодическая составляющая ре­шения для переходного процесса

(апериодическая степень устойчивости η).

Время ее за­тухания

характеризует общую длительность переходного процес­са, так как все члены решения, соответствующие осталь­ным корням, затухают быстрее.

Если же ближайшей к мнимой оси окажется пара комплексных корней (рис. 5.11, б), то доминирующая со­ставляющая решения для переходного процесса

будет колебательной (колебательная степень устойчиво­сти η), причем оценка длительности переходного про­цесса t_п остается прежней (5.9).

Определяется величина степени устойчивости следую­щим образом. Вводится новая комплексная переменная z = λ + η (рис. 5.12). Тогда на плоскости z мнимая ось β΄ пройдет через ближайшие корни, т. е. составленное относительно z характеристическое уравнение должно удовлетворять условию нахождения на границе устойчивости.

Таким образом, если задано характеристическое уравнение

то подставив λ = z — η , а именно

получим новое уравнение, которое называется смещен­ным, в виде

где коэффициенты A₁, A₂ , ..., A_n являются функциями η. Их можно вычислить следующим образом:

что вытекает из представления выражения (5.11) как

результата разложения функции D(λ) (5.10) при λ = z - η в ряд Тейлора.

З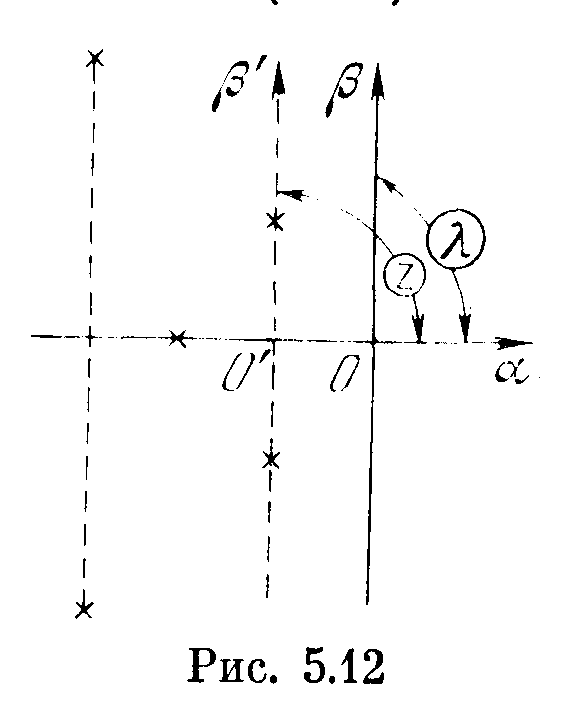атем к уравнению (5.11) приме­няется условие границ устойчивости, например, по Гурвицу

откуда и определяется величина η. Ниже будет дана диаграмма степени устойчивости для системы третьего порядка.

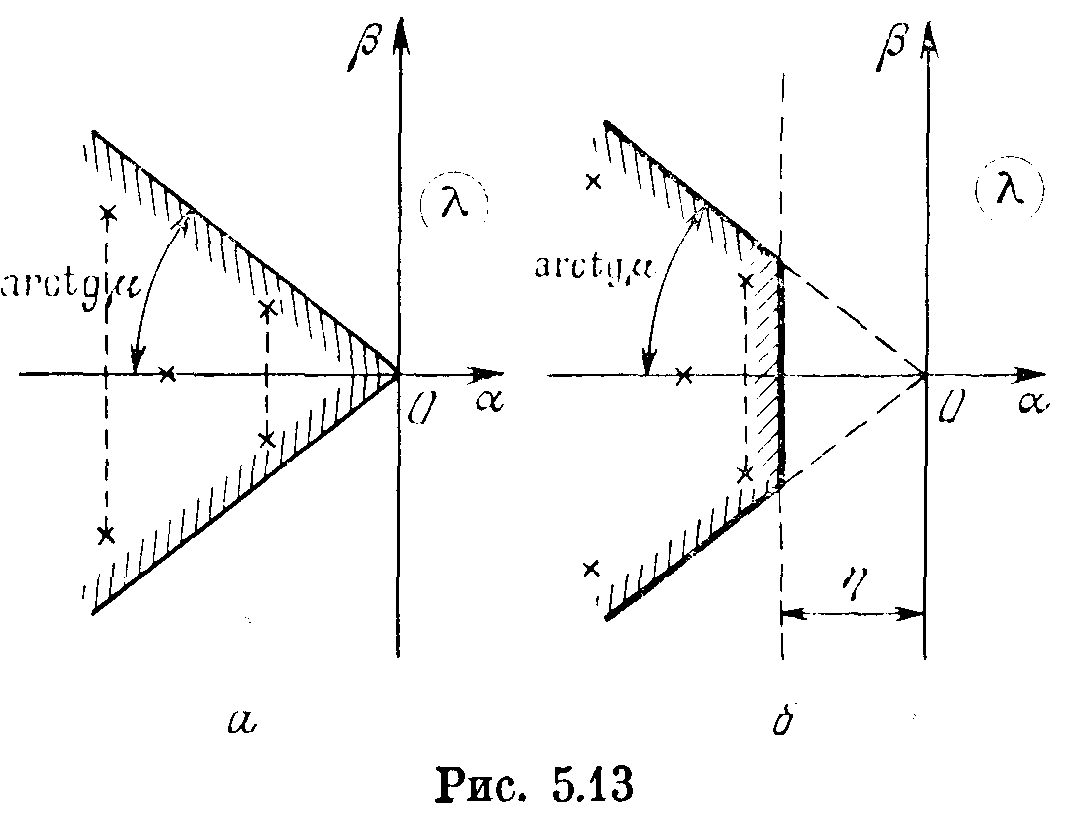
Колебательность переходного процесса определяется величиной

где α и β — вещественная и мнимая части корней харак­теристического уравнения. Именно эта величина харак­теризует быстроту затухания колебаний за каждый пе­риод. В самом деле, паре комплексных корней λ_{1 , 2} = -|α| ± jβ соответствует составляющая решения пере­ходного процесса

Период колебаний равен

Через один период амплитуда C₁ e ^{– | α | t} уменьшается до величины

Следовательно, чем больше величина , названная колебательностью, тем слабое будет затухание коле­баний в переходном процессе. Линия μ = const образует центральный угол (рис. 5.13, а) на комплексной пло­скости.

Суммарное требование определенных значений степе­ни устойчивости η и колебательности μ приводит к обла­сти, изображенной на рис. 5.13, б, внутри которой должны лежать все корни характеристического уравнения замк­нутой системы.

Далее необходимо иметь в виду, что для определения качества переходного процесса при единичном скачке внешнего воздействия существенны не только корни ха­рактеристического уравнения, т. е. полюса, по также и нули передаточной функции замкнутой системы Ф(s). В самом деле, как мы знаем,

Воспользуемся формулой (3.10), разложив многочлен N(s_i) на множители

где s_i = λ_i полюса Ф(s), т. е. корни характеристического уравнения D(λ) = 0; через N₁, N₂, ..., N_m обозначены ну­ли (корпи) многочлена N(s).

Отсюда видно, что амплитуды отклонений в переход­ном процессе, стоящие под знаком суммы, будут тем меньше, чем ближе расположены нули N_j к полюсам s_i т. е. корпи многочлена N(s) к корням характеристиче­ского уравнения. Именно в этом случае величины (s_i — N_j) будут малы. Это соответствует, напри­мер, схеме рис. 5.14, где нули обозна­чены кружочками. Заметим, что нули для замкнутой системы совпадают с ну­лями разомкнутой цепиW(s), так как

а полюса Ф(s) и W(s) существенно отличаются друг от друга.

Итак, для уменьшения амплитуд от­клонений в переходном процессе жела­тельно, чтобы нули передаточной функции замкнутой си­стемы Ф(s) располагались вблизи ее полюсов.

Примером корневых оценок качества переходного про­цесса в системах третьего порядка является диаграмма Вышнеградского (дана в его работе 1876 г., положившей начало развитию теории автоматического регулирования).

Характеристическое уравнение системы третьего по­рядка

приводится к нормированному виду

Параметры Вышнеградского А и В представляют, сле­довательно, определенные комбинации реальных парамет­ров системы, входящих в коэффициенты характеристиче­ского уравнения.

На плоскости параметров А, В граница устойчивости выразится зависимостью АВ = 1 (гипербола). Область устойчивости АВ > 1 разбивается на три подобласти (рис. 5.15) с различным расположением корней характе­ристического уравнения и соответственно — очертаний переходного процесса.

При этом граничные линии СЕ и CF находятся приравниванием нулю дискриминанта фор­мулы Кардана (решения кубического уравнения) в виде

а линия CD — из равенства вещественных частей всех корней —

В точке С (3; 3) все три корня вещественны и равны —1.

Позднее на диаграмму Вышнеградского были нанесе­ны линии равных значений степени устойчивости η и линии равных значений колебательности μ.

При определении степени устойчивости смещенное уравнение для нормированного характеристического урав­нения (5.16) будет

где согласно формулам (5.12)

Два условия (5.13) принимают соответственно вид

Полагая η = const, нанесем линии равных значений η на плоскость параметров Вышнеградского А, В. При этом согласно уравнению (5.18) получим для разных конкрет­ных значений η прямые линии, а согласно уравнениям (5.19) — кривые (рис. 5.16).

Для определения линий равных значений величины колебательности μ системы третьего порядка (5.16), ког­да корни его

имея в виду, что μ = β₁ /α₁ , по формулам Виета запишем

Исключая α₁ и α₂, обозначив x = 1 + μ², получим уравнение

которое позволяет построить на поле диаграммы Вышнеградского АВ линии равных значений μ = (рис. 5.17) в областях, где имеются комплексные корни. Если нам требуется в системе третьего порядка вы­брать параметры так, чтобы получить заданное качество

переходного процесса по показателям η и μ, мы выби­раем на рис. 5.16 и 5.17 соответствующую точку. Найдя таким образом значения А и B, пользуемся затем фор­мулами (5.17) для подбора параметров системы (5.15).