§ 5.2. Частотные оценки качества

Простейшей из частотных оценок качества переходного процесса является запас устойчивости. Он определяет только степень близости замкнутой системы к границе устойчивости по виду частотных характеристик ее разомкнутой цепи.

На рис. 5.3, а показано, как находить запас по амплитуде ΔLm и запас по фазе Δφ по логарифмическим частотным характеристикам. Если перенести их на амплитудно-фазовую частотную характеристику, то это будет соответственно ΔA и Δφ (рис. 5.3, б).

Длительность переходного процесса и перерегулиро­вание можно приближенно оценить по виду вещественной частотной характеристики замкнутой системы Р(ω). По­лучение ее рассмотрено выше в § 2.4.

На основании зависимости (5.5) выведены следующие оценки.

В переходном процессе получится перерегулирование σ > 18%, если Р(ω) имеет «горб» (рис. 5.4, а). При от­сутствии «горба» (рис. 5.4, б) будет σ < 18%. Процесс окажется наверняка монотонным (σ = 0), если монотонно убывает по абсолютному значению (рис. 5.4, б).

Длительность переходного процесса t_п оценивается приблизительно по величине интервала существенных ча­стот ω_сч (рис. 5.4), причем

Важно отметить, что время t_п обратно пропорционально величине ω_сч, т. е. чем более растянута частотная харак­теристика, тем короче переходный процесс. Физически это связано с тем, что, чем более высокие частоты «про­пускает» система, тем она менее инерционна в своих реакциях на внешние воздействия.

Это же свойство позволяет связать время t_п с часто­той среза ω_c (рис. 5.3) характеристики разомкнутой це­пи. Длительность переходного процесса t_п тем меньше, чем больше частота среза ω_c. Зависимость между величи­нами σ, t_п ,ω_c и Р_max представлена графиком на рис. 5.5.

Кроме того, свойство частотных характеристик тако­во, что начальная их часть влияет в основном на очерта­ние конца переходного процесса x(t), причем Р(0) = x_ус (рис. 5.4). Основное же влияние на качество переходного процесса оказывает форма средней части частотной ха­рактеристики.

В связи с этим логарифмическую частотную характе­ристику разомкнутой цепи системы Lm(ω) делят на три области (рис. 5.6), причем область низких частот в ос­новном определяет точность в установившемся режиме (в частности, астатизм и установившуюся ошибку на рабочей частоте следящей системы). Область средних ча­стот в основном определяет качество переходного процес­са. В частности, частота среза ω_c, как уже говорилось,

определяет полосу пропускания сигналов и длительность переходного процесса. Наклон Lm(ω) вблизи частоты среза ω_c характеризует колебательность переходного про­цесса. Так, наклон —20 дБ/дек при ω = ω_c (рис. 5.6), соответствующий свойст­вам апериодического зве­на, обеспечивает наимень­шую колебательность пере­ходного процесса в замкну­той системе.

Следующей частотной оценкой качества является показатель колебательно­сти — максимальное значе­ние M_max , амплитудной ча­стотной характеристики замкнутой системы (рис. 5.7)

Эта величина M_max может быть определена по виду частотной характеристики разомкнутой цепи данной си­стемы. В самом деле

Следовательно, линии равных значений величины М, нанесенные на плоскости W(jω), будут окружностями со смещающимся центром С и меняющимся радиусом R, как показано на рис. 5.8.

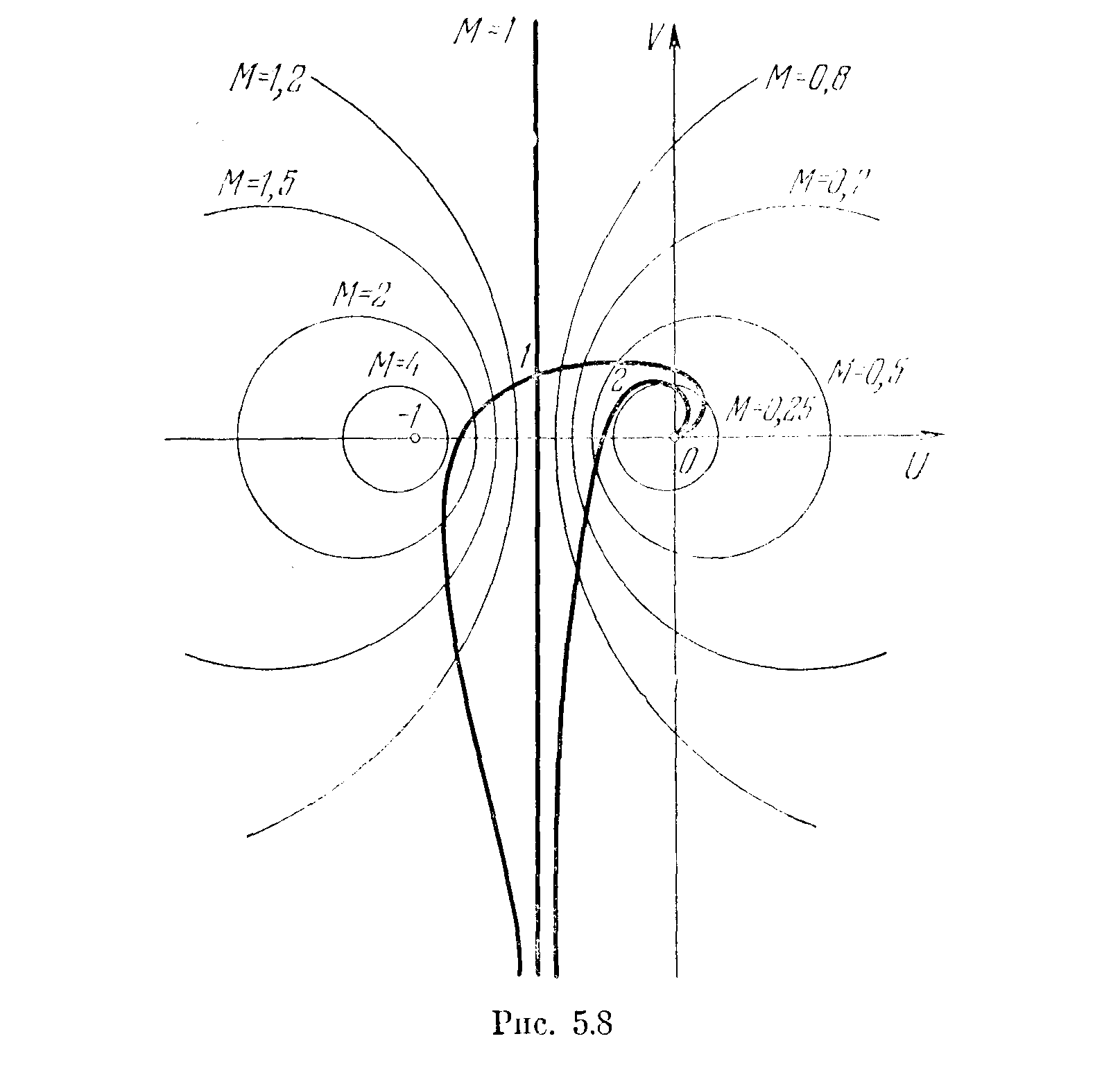
Имея такую диаграмму линий М = const, можно по заданной амплитудно-фазовой характеристике разомкну­той цепи W(jω) легко определить показатель колеба­тельности замкнутой системы M_max и построить нею амп­литудную частотную характеристику M=|Ф( jω)| замк­нутой системы (рис. 5.7).

Изображенные на рис. 5.8 характеристики W(jω) (1 и 2) соответствуют характеристикам 1 и 2 замкнутой системы |Ф( jω)| (рис. 5.7).

Если, например, желательно иметь M_max < 1,5 , то ха­рактеристику 1 (рис. 5.8) нужно скорректировать так, чтобы она не заходила внутрь круга М = 1,5 (рис. 5.9).

Такую запретную область можно перенести на пло­скость логарифмической частотной характеристики сле­дующим образом. На кривой М = 1,5 (рис. 5.9) в каждой

точке имеем определенное значение амплитуды А и фа­зы φ. Следовательно, зная Lm(ω) (рис. 5.10), можем для каждого значения Lm = 20 lgА отметить там соот­ветствующую точку φ. Таким образом, образуется кривая М = 1,5 на поле логарифмических характеристик, очер­чивающая запретную зону, в которую не должна захо­дить фазовая частотная характеристика φ(ω).