§ 3.5. Чувствительность автоматических систем

Параметры системы автоматического управления, т. е. коэффициенты усиления и постоянные времени, зависят от физических параметров элементов, входящих в систе­му (сопротивления, емкости, индуктивности и т. п.). Ве­личины этих физических параметров, во-первых, могут иметь разброс вследствие допусков на изготовление {тех­нологический разброс}. Во-вторых, в зависимости от ус­ловий эксплуатации в процессе работы системы они по разным причинам могут изменяться со временем (эксплуатационное изменение).

Поэтому возникает задача определения влияния раз­броса и изменения параметров системы на статические и динамические свойства процесса управления, т. е. на точность системы, на временные характеристики (пока­затели качества переходных процессов) и на частотные характеристики.

Степень влияния разброса и изменения параметров системы на ее статические и динамические свойства на­зывается чувствительностью системы. Чувствительность определяется количественно. Существуют методы ее ана­лиза и методы достижения малой чувствительности про­ектируемой системы к разбросу и изменению некоторых ее параметров, когда это требуется.

Пусть система описывается уравнениями в нормаль­ной форме (2.21), т. е.

где x_i — координаты состояния системы. Изменяющиеся со временем параметры системы в процессе ее эксплуата­ции и от разброса при изготовлении обозначим через

Они входят в коэффициенты уравнения (3.36).

Поэтому уравнения системы (3.36) можно представить в следующей общей форме:

Рассматривая малые изменения параметров, получим новые уравнения

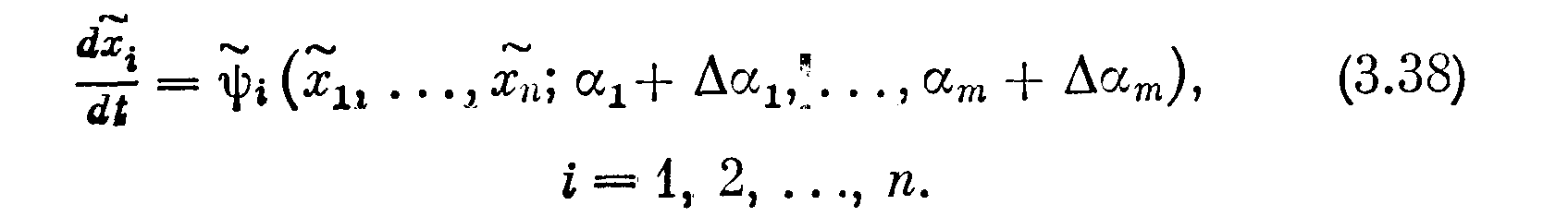
Процесс в системе (3.37) при неизменных параметрах, определяемый ее решением

называется исходным движением.

Процесс в той же системе, но с измененными пара­метрами, определяемый решением уравнений (3.38), т. е.

называется варьированным движением.

Возникает различие в протекании этих процессов за счет изменения параметров системы

которое называется дополнительным движением системы. При малых изменениях параметров α_j можно записать

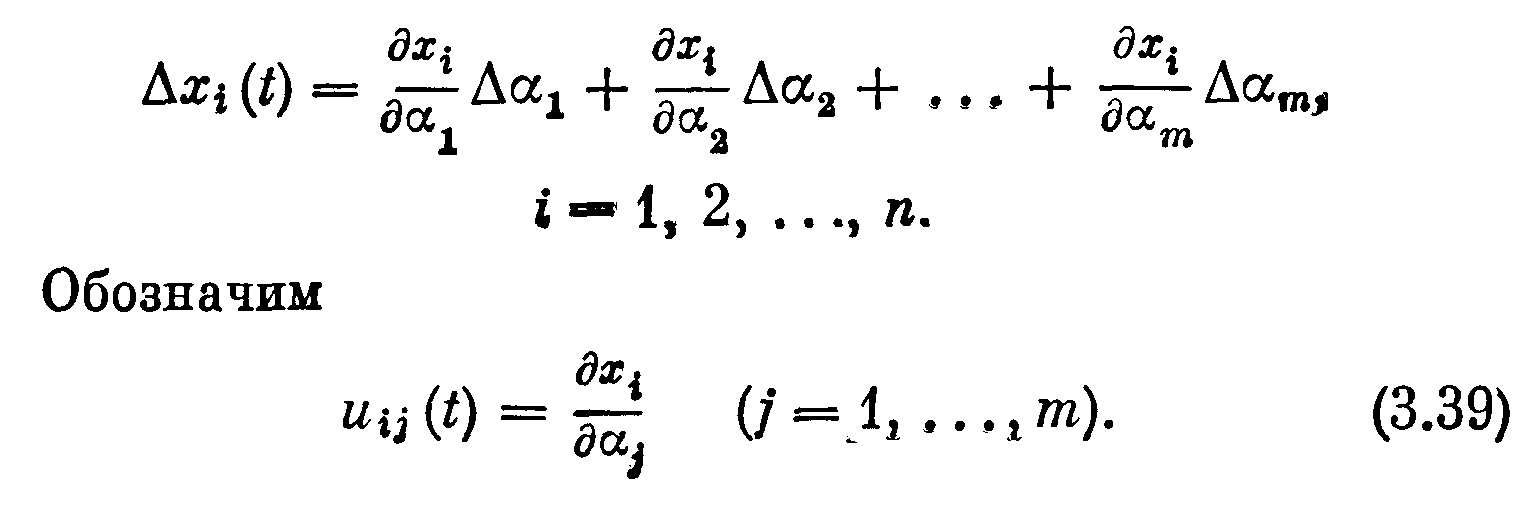
Тогда дополнительное движение будет

Величины u_{i j} ( t ), определяемые формулой (3.39), на­зываются функциями чувствительности.

В данном случае x_i являются координатами состояния системы. Вообще же аналогичные характеристики чув­ствительности вводятся так же и для различных показа­телей качества системы. Тогда в формуле (3.39) вместо x_i будет стоять соответствующий показатель качества, а в формуле (3.40) — вместо Δx_i —изменение этого показа­теля качества. Функции чувствительности для частотных характеристик будут функциями не времени, а частоты ω. Когда же показатель качества выражается не функцией, а числом, то u_ij называются уже не функциями, а коэф­фициентами чувствительности. Последние определяются как при эксплуатационном изменении параметров, так и при их технологическом разбросе.

Определение функций чувствительности производится следующим образом.

Продифференцируем исходное уравнение (3.37) по параметрам α _j. Получим

Меняя в левой части порядок дифференцирования и учитывая формулу (3.39), получим выражения

которые называются уравнениями чувствительности. Не­посредственное определение функций чувствительности u_ij по этим уравнениям затруднительно. Поэтому приме­няют косвенные методы, например, с помощью моделей [31] или графов [5].

Приведем простейший пример определения уравнений чувствительности для системы

Введем две функции чувствительности

Уравнение данной системы в нормальной форме имеет вид

Отсюда по формуле (3.41) получим

Это и будут уравнения чувствительности такой про­стейшей системы. Вычислив отсюда и_K и и_T, найдем из­менение хода процесса управления за счет эксплуатаци­онного изменения параметров К и Т по формуле

Что же касается функций и коэффициентов чувстви­тельности для показателей качества, то их определение проще, поскольку там не будет дифференциальных урав­нений.

Рассмотрим функции чувствительности частотных ха­рактеристик.

Запишем передаточную функцию разомкнутой цепи системы

где α₁, α₂, ..., α_m — параметры системы, имеющие тех­нологический разброс или эксплуатационные изменения. После подстановки s = jω запишем выражения амплитуд­ной и фазовой частотных характеристик

Функции чувствительности здесь будут

В результате вместо формул (3.40) здесь получим как функции частоты о формулы для отклонения частотных характеристик за счет разброса и изменения параметров системы:

В частности, для приведенного выше простейшего примера имеем

Найдем функции чувствительности частотных харак­теристик по параметру α₁ = Т. Поскольку здесь

то функции чувствительности (3.42) будут

Отклонения частотных характеристик согласно (3.43) получат значения

Определение функций чувствительности применяется для проектирования системы с наименьшим изменением качественных показателей при отклонении значений па­раметров системы от расчетных.

Аналогично можно находить также функции или ко­эффициенты чувствительности для нулей и полюсов пе­редаточной функции при корневых методах исследования, а также для других показателей качества.