§ 3.4. Установившаяся ошибка при произвольном воздействии (коэффициенты ошибок)

В общем случае изображение ошибки ε(t) воспроиз­ведения задающего воздействия g(t) выражается фор­мулой

Передаточную функцию можно (см. § 1.1) определить как преобразование Лапласа весовой функции

где k_ε(t)— весовая функция для ошибки, т. е. реакция замкнутой системы в точке измерения ошибки (рассогла­сования) на мгновенный единичный импульс внешнего задающего воздействия g(t) = δ(t).

Величину установившейся ошибки при произвольной форме задающего воздействия (см. § 3.1) можно записать в виде

Последнее выражение следует из того, что при τ > t аргумент функции g(t - τ) будет отрицательным, а при отрицательном значении t - τ принимается g(t - τ)=0. Поэтому замена конечного предела t бесконечным не ме­няет результата.

Разложим g(t - τ) в ряд:

Подставив это в соотношение (3.26), получим выра­жение вида

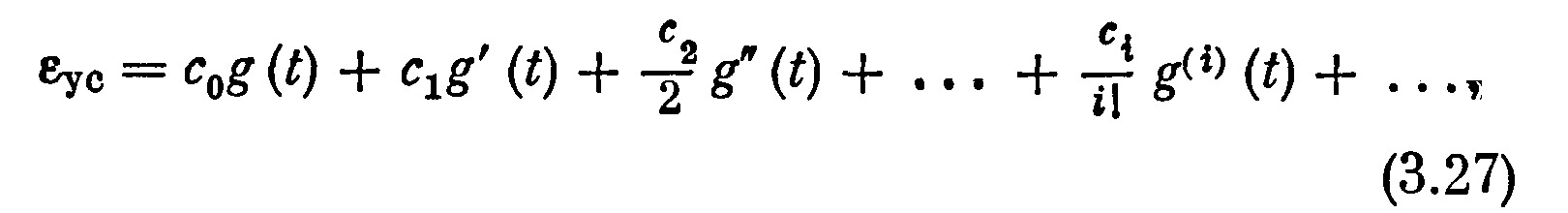
где коэффициенты c₀, c₁ , ... определяются из (3.26) сле­дующим образом. Очевидно,

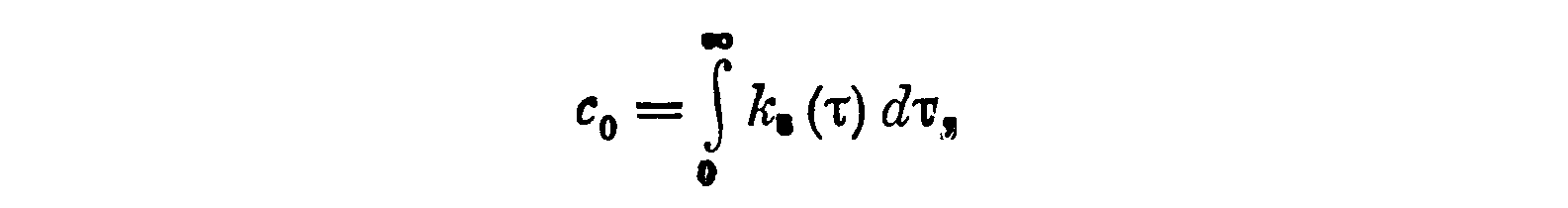
поэтому согласно формуле (3.25) имеем

Аналогично из (3.26) получаем

и согласно (3.25) находим

и т. д.

Общий член разложения (3.27) согласно (3.26) будет иметь коэффициент

или на основании (3.25)

Итак, установившаяся ошибка при произвольном за­дающем воздействии g(t) определяется формулой (3.27) с коэффициентами (3.28)—(3.30). Последние называются коэффициентами ошибок.

На практике ограничиваются небольшим конечным числом членов i.

Вычисление коэффициентов ошибок непосредственно по формулам (3.28)—(3.30) неудобно. Поэтому практически применяется другой способ, который вытекает из сле­дующего рассуждения.

Разложим передаточную функцию Ф_ε(s) в ряд

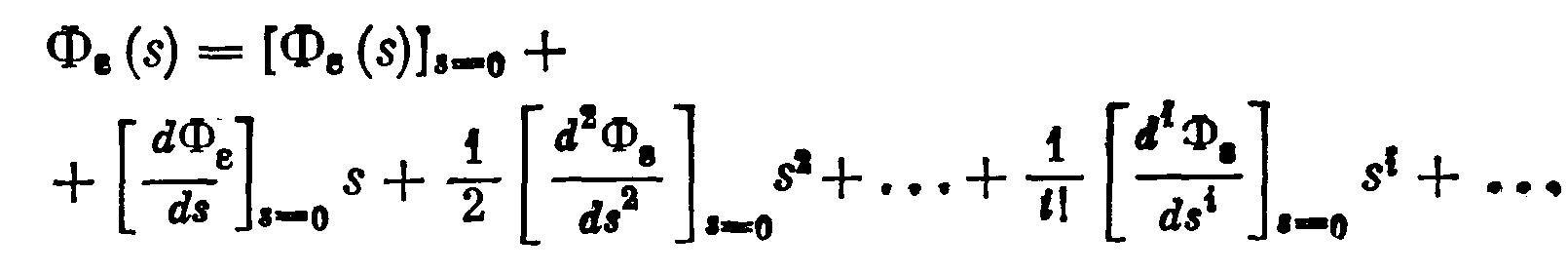
Как видно, в этом разложении фигурируют выраже­ния для коэффициентов ошибок (3.28)—(3.39). Следо­вательно,

Но Ф_ε(s) является отношением многочленов, т. е.

Очевидно, что произведя простое деление многочлена числителя (3.32) на многочлен знаменателя по известно­му алгебраическому правилу, мы и получим выражение

типа (3.31), а значит, и значения всех коэффициентов ошибок.

После этого, подставив (3.31) в формулу

и переходя к оригиналам, получим

что совпадает с ранее полученным (3.27).

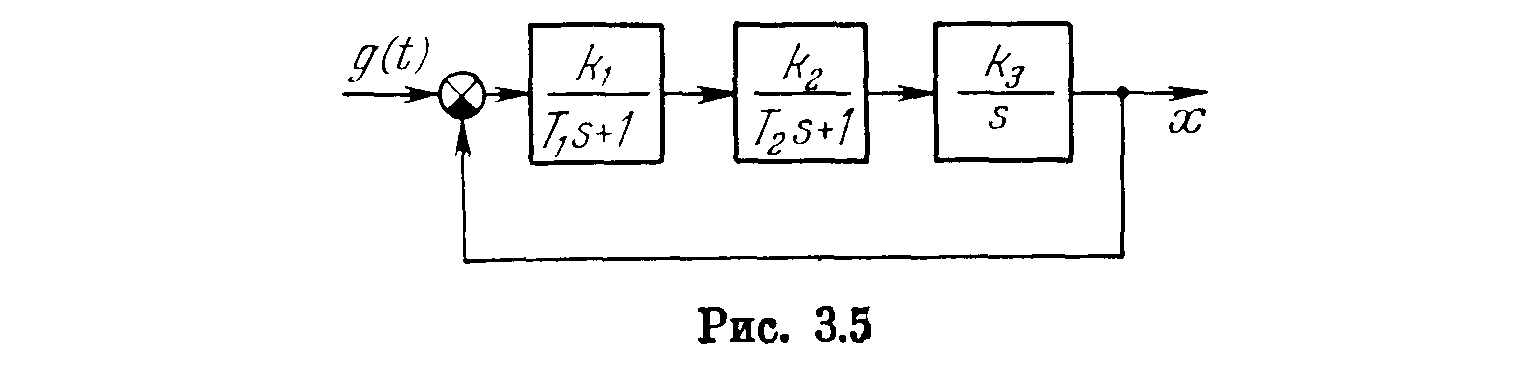
Пример. Для системы с астатизмом первого порядка, схема которой дана на рис. 3.5, имеем

Следовательно,

Разделив числитель на знаменатель, получаем

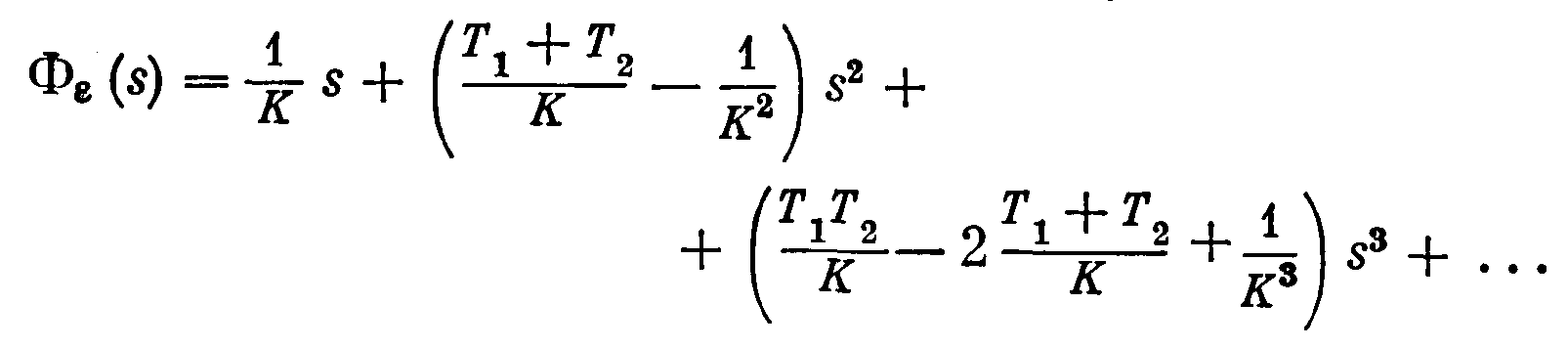
Отсюда, сравнивая с (3.31), находим коэффициенты ошибок

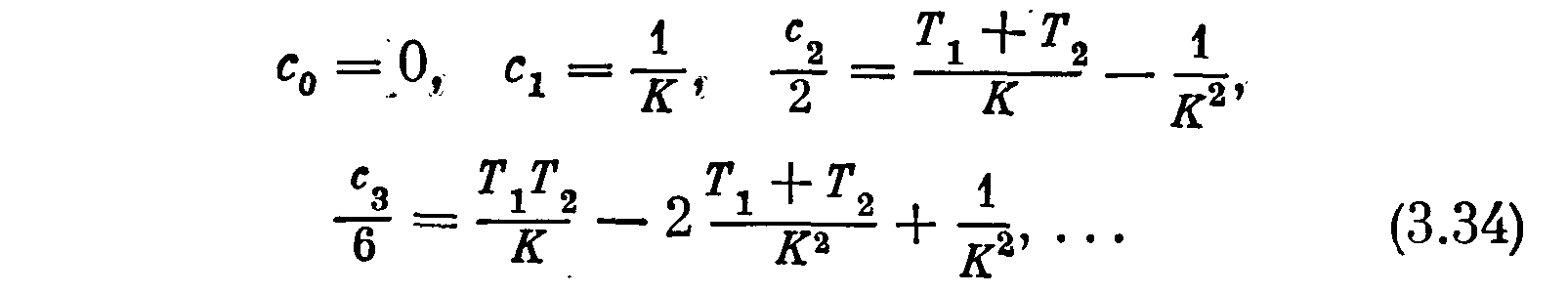
Поскольку коэффициент усиления К находится в зна­менателе, а постоянные времени Т в числителе, можно сделать вывод о том, что все ошибки уменьшаются с уве­личением К и с уменьшением постоянных времени, ха­рактеризующих инерционность системы.

Из приведенного примера видно, что коэффициент c₀ соответствует статической, a c₁ — скоростной ошибкам, которые рассматривались ранее в § 3.2.

Допустим, задающее воздействие имеет вид

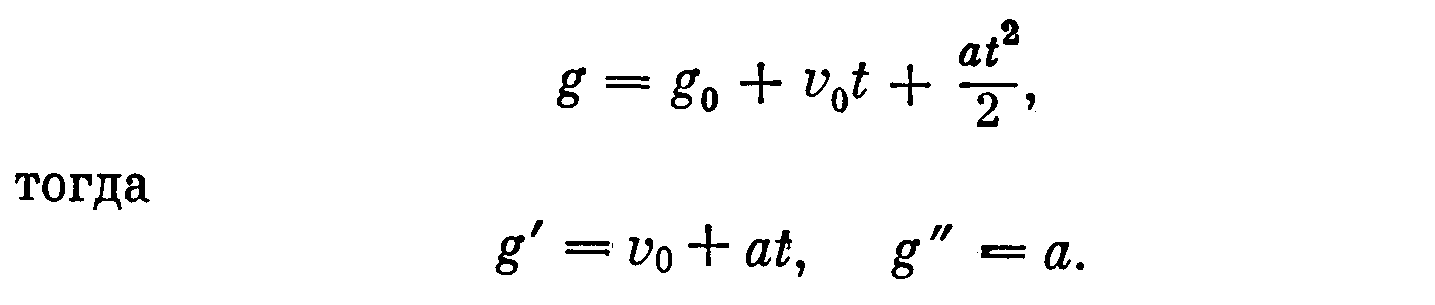
По формуле (3.27) с найденными коэффициентами получаем

Важно отметить, что при произвольном внешнем воз­действии в формулах для ошибок общий коэффициент усиления разомкнутой цепи К (добротность) влечет за собой уменьшение всех видов установившихся ошибок замкнутой системы. Это главный фактор повышения точности замкнутой системы автоматического управ­ления.

Необходимо заметить, что вычисление установившихся ошибок по указанным формулам имеет практический смысл при достаточно медленном изменении внешнего воздействия. Иначе эта ошибка не будет реальной из-за наличия значительной переходной составляющей про­цесса.

Отметим также, что выше определялись коэффициен­ты ошибок по задающему воздействию. Аналогично это можно сделать и по возмущающим воздействиям, при­влекая соответствующие передаточные функции.