Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Петрозаводский государственный университет»

Расчет траектории электрона, влетающего в магнитную линзу

Курсовой проект по математическому моделированию

Выполнил: студент 2 курса

физико-технического факультета, гр.21212

Воробьев Кирилл Игоревич

Проверил:

Старший преподаватель КИИСиФЭ,

Екимов Дмитрий Анатольевич

Петрозаводск 2012

Содержание отчета

Формулировка задачи -------------------------------------------------------------- 3

Теоретические основы решения задачи ---------------------------------------- 3

Словесно-формульный алгоритм ------------------------------------------------ 6

Листинг программы ----------------------------------------------------------------- 9

Результат выполнения программы ---------------------------------------------- 13

Литература --------------------------------------------------------------------------- 14

Формулировка задачи Вариант 14

Рассчитать траекторию электрона, влетающего в магнитную линзу параллельно оси на расстоянии от оси 0.2 см с начальной скоростью 10⁹ см/с.

Iω = 100 А*виток

d1 = 1.8 см

d2 = 3.2 см

h = 0.5 см

Теоретические основы решения задачи Вычисление индукции магнитного поля

Если катушку нельзя считать короткой, то индукция магнитного поля в точке на оси Z находится суммированием от каждого витка в отдельности (рис. 2):

, где (1)

ток, текущий в одном витке;

радиус витков i-го слоя вдоль оси r;

соответственно внешний и внутренний радиусы катушки;

расстояние от точки z, в которой рассчитывается поле, до плоскости, в которой расположен j-й слой витков вдоль оси Z;

h  толщина катушки.

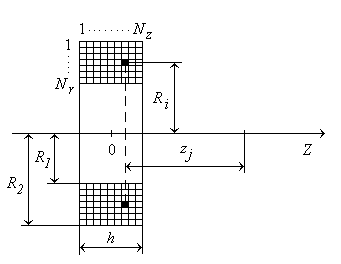
Рис. 2.

В приосевой области для нахождения проекций вектора магнитной индукции можно воспользоваться разложением в ряд Щерцера (цилиндрическая система координат):

(2)

, где

и  проекции магнитной индукции на оси r и z.

Значение первой производной по z можно оценить следующим образом:

(3)

Интегрирование уравнений движения

В случае нерелятивистской задачи с магнитным полем уравнения движения в цилиндрической системе координат при имеют вид:

(4)

Численное интегрирование можно провести следующим образом (схема типа предиктор-корректор). Предварительно находится приближенное значение угловой скорости на шаге (n+1):

(5)

Значения относятся к промежуточной точке с координатами:

(6)

Поскольку при не определена, то для достаточно малых r полагаем .

Далее вычисляем значения скоростей на и шаге:

(7)

(8)

После этого корректируем значение угловой скорости:

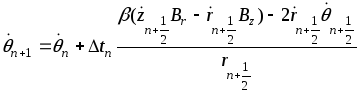(9)

и находим координаты частицы на шаге:

(10)