Федеральное агентство по образованию

Государственное Образовательное Учреждение Высшего Профессионального Образования

“Тверской государственный технический университет”

(ГОУ ВПО ”ТГТУ”)

Кафедра Информационных систем

Курсовая работа по дисциплине

«Теория вероятность и математическая статистика»

Выполнил студент 2 курса

Петров А.А.

Проверил профессор кафедры ИС

Ветров А. Н.

Оценка:__________

Подпись:__________

Тверь 2012 г

Оглавление

1.Введение 2

2.Предельные теоремы 3

2.1.Теорема Бернулли 4

2.2.Закон больших чисел Чебышева. 5

3.Простая линейная регрессия 6

4.ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ. 9

4.1.Двухвыборочный z-тест для средних 9

5. Заключение 12

1. Введение

Темой данной курсовой работы являлось определение и проверка вероятности предельных теорем, а именно Теоремы Бернулли и Закона больших чисел Чебышева, определения коэффициентов простой линейной регрессии, полученных в ходе проведённых испытаний и проверки статистических гипотез.

В проверки предельных теорем мы проведём тесты для определения вероятности выпадения «герба» с большим числом опытов (для Теоремы Бернулли это число составит 170 и 1850 опытов соответственно), а также проведём анализ Закона больших чисел с целью определения случайных величин при большом nопытов.

Для уравнения линейной регрессии найдём коэффициенты a₀и a₁ а также найдём определим коэффициент корреляции r_yx при помощи генерации числа  случайным образом в интервале [0,1].В следствии чего проверим качество подгонки(степень тесноты) регрессионной модели к наблюдаемым данным по шкале Чеддока.

Для проверки статистических гипотез проведём несколько тестов для проверки двух собственных гипотез: «H₀: m_x=m_y и H₁: m_x≠m_y».

И сделаем заключение по полученным данным.

2. Предельные теоремы

1. Теорема Бернулли

Если проводится n независимых испытаний случайного события A, вероятность которого P(A) = p, то относительная частота m/n появления события A (mчисло появлений A) при большом n приближенно равна вероятности p:

.

уточнение: будем писать

при ,

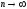если для любого >0 и для достаточно больших n соотношение

(1)

выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:

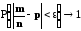при .

f_n– 0.5<0.1 при n = 170 и f_n– 0.5<0.03 при n=1850.

N= 170 опытов
Случай	1	2	3	4	5
кол-во выпадений “герба”	82	84	94	87	88
вероятность выпадения	0,01765	-0,00588	0,052941	-0,50003	0,017647

N= 1850 опытов
Случай	1	2	3	4	5
кол-во выпадений “герба”	896	943	918	902	915
вероятность выпадения	-0,01568	0,00973	-0,00378	-0,01243	0,00541

Вывод. При n=170 теорема Бернулли выполняется в 5 опытах из 5, а при n=1850 в 5 опытах.

2. Закон больших чисел Чебышева.

Одно из основных утверждений закона больших чисел состоит в том, что значение среднеарифметического случайных величин с равными математическими ожиданиями, при большом n оказывается приближенно равным a:

Будем писать

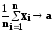при ,

если для любого >0 и достаточно больших n соотношение

(2)

выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:

при .

Проверяем (2) на достоверность:

N= 45 опытов
Случай	1	2	3	4	5
кол-во выпадений “герба”	16	16	26	28	22
вероятность выпадения	0.959932	0.919688	0.079384	1.04187	0.100883

N= 1125 опытов
Случай	1	2	3	4	5
кол-во выпадений “герба”	582	556	555	536	546
вероятность выпадения	0.013778	0.00311	0.011111	0.0173333	0.02089

Вывод. Для N=45 закон больших чисел выполняется при P=-0.4943, для N=1125 при P=0.49973.