
- •Внимание!!! контрольная работа должна быть выполнена в рукописном виде. Иначе она принята не будет. Варианты с 6 по 10.
- •1. Типы уравнений второго порядка в частных производных. Приведение к каноническому виду
- •Задания для самостоятельной работы
- •Составим уравнение движения струны. На элемент струны (х,) действуют силы натяженияи внешняя сила, действующая на струну в точкехв момент времениtи направленная перпендикулярно осиОх.
- •2.2. Формула Даламбера
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •2.5. Решение краевой задачи методом Фурье
- •Задания для самостоятельной работы
- •3.2. Решение краевых задач методом Фурье
- •3.3. Неоднородное уравнение теплопроводности Рассмотрим задачу для неоднородного уравнения теплопроводности
- •Задания для самостоятельной работы
- •3.5. Решение уравнения теплопроводности методом Тейлора
- •Задания для самостоятельной работы
- •Или. (158)
- •Задания для самостоятельной работы
3.2. Решение краевых задач методом Фурье
Рассмотрим
задачу отыскания нестационарного
температурного поля u(x,t)
в плоском слое конечной толщины l,
имеющим в начальный момент времени
температуру
![]() ,
если на поверхностяхx=0
и l=0
этого слоя происходит теплообмен с
окружающей средой, имеющей нулевую
температуру. Требуется найти решение
однородного линейного параболического
уравнения
,
если на поверхностяхx=0
и l=0
этого слоя происходит теплообмен с
окружающей средой, имеющей нулевую
температуру. Требуется найти решение
однородного линейного параболического
уравнения
![]() , (84)
, (84)
удовлетворяющее при t=0 начальному условию
![]() , (85)
, (85)
и однородным граничным условиям третьего рода
 (86)
(86)
Нетривиальные решения уравнения (84), удовлетворяющие граничным условиям (86), будем искать в виде
![]() . (87)
. (87)
Подставив эту форму решения в уравнение (84) и разделив переменные, получим
![]() .
.
Поэтому функции T(t) и X(x) можно найти как решения обыкновенных однородных дифференциальных уравнений вида
![]() ; (88)
; (88)
![]() . (89)
. (89)
Рассмотрим уравнение (89) с граничными условиями вида
 (90)
(90)
Задача
(89)-(90) является задачей Штурма-Лиувилля.
Для того, чтобы найти собственные
значения, необходимо найти нетривиальные
решения уравнения (89). Поскольку корни
характеристического уравнения,
соответствующего уравнению (89)
исключительно мнимые
![]() ,
то общее решение уравнения (89) имеет вид
,
то общее решение уравнения (89) имеет вид
![]() . (91)
. (91)
Вычислим производную от (91) и, удовлетворив краевым условиям (90), получим
![]() Из
первого равенства выразим С1
и подставим во второе уравнение
Из
первого равенства выразим С1
и подставим во второе уравнение

Из второго уравнения системы следует, что, если С2 =0, то и С1 тоже будет равна нулю. Следовательно, X(x) ≡ 0., поэтому нетривиальные решения уравнения (89) будут при условии, что
![]() . (92)
. (92)
Таким образом, задача Штурма-Лиувилля (89), (90) имеет нетривиальные решения только при определенных, собственных значениях
![]() (93)
(93)
которые
можно выразить через неотрицательные
корни
![]() ,
полученного из условия (92), трансцендентного
уравнения вида
,
полученного из условия (92), трансцендентного
уравнения вида
 .
.
Соответствующие
собственным значениям
![]() собственные функцииXn(x)
имеют вид
собственные функцииXn(x)
имеют вид
![]() . (94)
. (94)
Квадраты норм этих функций определяются выражением
 .
.
При
![]() =
=![]() уравнение (88) принимает вид
уравнение (88) принимает вид
![]() .
.
Общее решение этого однородного линейного уравнения имеет вид
![]() . (95)
. (95)
Таким образом, подставляя (94) и (95) в (87) получим частные решения уравнения (84), удовлетворяющие краевым условиям (86):
![]() . (96)
. (96)
На
основании принципа суперпозиции частных
решений
![]() следует, что общее решение уравнения
(84) может быть представлено в области
следует, что общее решение уравнения
(84) может быть представлено в области![]() в виде ряда
в виде ряда
![]() . (97)
. (97)
Рассмотрим частные случаи задачи (84)-(86).
1.
При значении параметров
![]() краевые условия принимают вид
краевые условия принимают вид
![]() (98)
(98)
и
краевая задача (84),(85), (98) описывает
процесс остывания плоского слоя конечной
толщины l
(или стержня конечной длины l
с идеально теплоизолированной боковой
поверхностью), с температурным профилем
![]() в начальный момент времени, если граничные
плоскостих=0
и x=l
(торцы стержня) поддерживаются при
постоянной нулевой температуре.
в начальный момент времени, если граничные
плоскостих=0
и x=l
(торцы стержня) поддерживаются при
постоянной нулевой температуре.
В этом случае собственные значения определяются выражением
![]() (99)
(99)
а собственные функции имеют вид
![]() . (100)
. (100)
Следовательно, решение данной краевой задачи определяется формулой
![]() , (101)
, (101)
где
![]() . (102)
. (102)
2.
При значении
параметров
![]() краевые условия принимают вид
краевые условия принимают вид
![]() . (103)
. (103)
В
этом случае краевая задача (84),(85), (103)
описывает процесс выравнивания
температуры в плоском слое (стержне), в
котором в начальный момент времени
задан температурный профиль
![]() ,
а граничные плоскостих=0
и x=l
(торцы стержня) идеально теплоизолированы.
,
а граничные плоскостих=0
и x=l
(торцы стержня) идеально теплоизолированы.
Для этого случая
![]() (104)
(104)
а собственные функции имеют вид
 (105)
(105)
Следовательно, решение данной краевой задачи определяется формулой
![]() , (106)
, (106)
где
![]() . (107)
. (107)
Необходимо отметить, что при t→∞ температура всех слоев выравнивается и стремиться к стационарному распределению
![]() .
.
3.
При значении параметров
![]() краевые условия принимают вид
краевые условия принимают вид
![]() . (108)
. (108)
В
этом случае смешанная краевая задача
(84),(85), (108) описывает эволюцию температурного
поля в плоском слое
![]() тела, начальное распределение температуры
в котором задано функцией
тела, начальное распределение температуры
в котором задано функцией![]() ,
если на поверхностих=0
поддерживается постоянная нулевая
температура, а на другой поверхности
x=l
происходит конвективный теплообмен с
окружающей средой, имеющей нулевую
температуру.
,
если на поверхностих=0
поддерживается постоянная нулевая
температура, а на другой поверхности
x=l
происходит конвективный теплообмен с
окружающей средой, имеющей нулевую
температуру.
Для этого случая
![]() (109)
(109)
а собственные функции имеют вид
![]() . (110)
. (110)
Значения
![]() являются действительными положительными
корнями трансцендентного уравнения:
являются действительными положительными
корнями трансцендентного уравнения:![]() .
.
Таким образом, решение смешанной краевой задачи определяется формулой
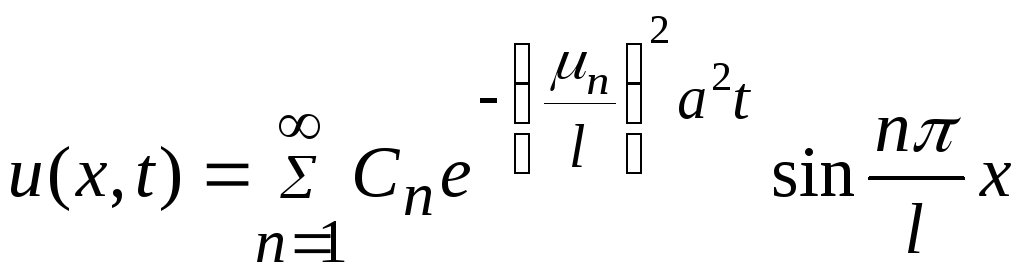 , (111)
, (111)
где
 . (112)
. (112)
