
- •Внимание!!! контрольная работа должна быть выполнена в рукописном виде. Иначе она принята не будет. Варианты с 6 по 10.
- •1. Типы уравнений второго порядка в частных производных. Приведение к каноническому виду
- •Задания для самостоятельной работы
- •Составим уравнение движения струны. На элемент струны (х,) действуют силы натяженияи внешняя сила, действующая на струну в точкехв момент времениtи направленная перпендикулярно осиОх.
- •2.2. Формула Даламбера
- •Задания для самостоятельной работы
- •Задания для самостоятельной работы
- •2.5. Решение краевой задачи методом Фурье
- •Задания для самостоятельной работы
- •3.2. Решение краевых задач методом Фурье
- •3.3. Неоднородное уравнение теплопроводности Рассмотрим задачу для неоднородного уравнения теплопроводности
- •Задания для самостоятельной работы
- •3.5. Решение уравнения теплопроводности методом Тейлора
- •Задания для самостоятельной работы
- •Или. (158)
- •Задания для самостоятельной работы
Задания для самостоятельной работы
Решить
краевую задачу для уравнения Лапласа
внутри круга
![]() со следующими граничными условиями:
со следующими граничными условиями:
42.
![]() .
.
43.
![]() .
.
44.
![]() .
.
45.
![]()
46.
![]()
Решить
краевую задачу для уравнения Лапласа
вне круга
![]() со следующими граничными условиями:
со следующими граничными условиями:
47.
![]() .
.
48.
![]() .
.
49.
![]() .
.
50.
![]() .
.
51.
![]() .
.
Ответы на задания для самостоятельной работы
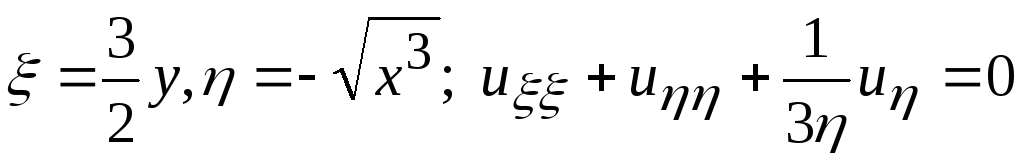 .
. .
3.
.
3. .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]() .
9.
.
9.![]() .
.
10.
![]() .
11.
.
11.![]() .
.
12.
![]() .
13.
.
13.![]() .
.
14.
![]() .
.
15.
![]() .
.
16.
![]() .
.
17.
![]() .
.
18.
![]() .
.
19.
![]() .
.
20.
![]() .
.
21.
![]() .
.
22.
 .
.
23.
![]() .
.
24.![]() .
.
25.
![]() .
.
26.
![]() .
.
27.
![]() .
.
28.
![]() .
.
29.
![]() .
.
30.
![]() .
31.
.
31.![]() .
.
32.![]() .
33.
.
33.![]()
34.
![]() .
35.
.
35.![]() .
.
36.
![]() .
.
37.
![]() .
.
38.
![]() .
.
39.
![]() .
.
40.
![]() .
.
41.
![]() .
.
42.
![]() .
.
43.
![]() .
.
44.
![]() .
45.
.
45.![]() .
.
46.
![]() .
.
47.
![]() .
.
48.
![]() .
49.
.
49.![]() .
.
50.
![]() .
51.
.
51.![]() .
.
ВНИМАНИЕ, КОНТРОЛЬНЫЕ РАБОТЫ ДОЛЖНЫ БЫТЬ НАПИСАНЫ ОТ РУКИ. В НАПЕЧАТАННОМ ВИДЕ РАБОТЫ ПРИНИМАТЬСЯ НЕ БУДУТ!
КОНТРОЛЬНЫЕ РАБОТЫ
I. ПРИВЕДЕНИЕ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ
Вариант №1
Привести уравнения к каноническому виду
 .
. .
. .
.
Вариант №2
Привести уравнения к каноническому виду:
 .
. .
.
3.
![]() .
.
Вариант №3
Привести уравнения к каноническому виду:
 .
. .
. .
.
Вариант №4
Привести уравнения к каноническому виду:
 .
. .
. .
.
Вариант №5
Привести уравнения к каноническому виду:
 .
. .
. .
.
Вариант №6
Привести уравнения к каноническому виду:
1.
![]() .
.
2.
![]() .
.
Вариант №7
Привести уравнения к каноническому виду:
1.
![]() .
.
2.
![]() .
.
Вариант №8
Привести уравнения к каноническому виду:
1.
![]() .
.
2.
![]() .
.
Вариант №9
Привести уравнения к каноническому виду:
1.
![]() .
.
2.![]() .
.
Вариант №10
Привести уравнения к каноническому виду:
1.
![]() .
.
2.
![]() .
.
II. МЕТОД ХАРАКТЕРИСТИК
Вариант №1
Найти общее решение уравнений:
 .
.
 .
.
Вариант №2
Найти общее решение уравнения:
 .
. .
. .
.
Вариант №3
Найти общее решение уравнений:
 .
. .
.
Вариант №4
Найти общее решение уравнений:

 .
. .
.
Вариант №5
Найти общее решение уравнений:
 .
.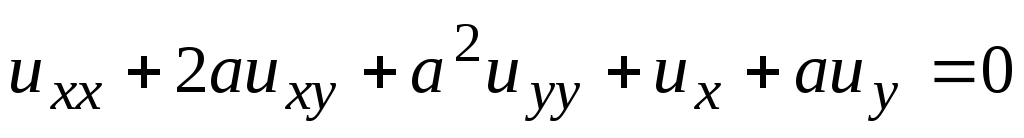 .
.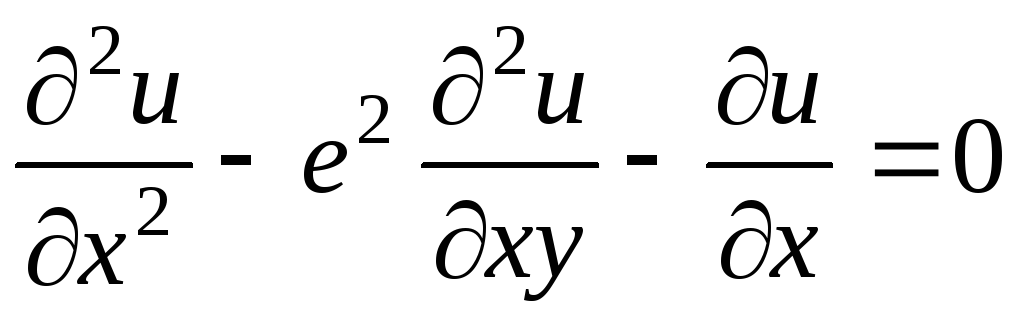 .
.
Вариант №6
Найти общее решение уравнений:
 .
.
2.
![]() .
.
3.
![]() .
.
Вариант №7
Найти общее решение уравнений:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Вариант №8
Найти общее решение уравнений:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Вариант №9
Найти общее решение уравнений:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
Вариант №10
Найти общее решение уравнений:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
III. УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Вариант №1
Решить задачу Коши:
 .
. ;
;
 ,
, .
. .
.
Решить граничную задачу:
 .
.
6.
![]()
Вариант №2
Решить задачу Коши:
 .
. ;
;
 ,
, .
. .
. ;
;
 ,
, .
.
Решить граничную задачу:
 .
.
6.
![]() .
.
Вариант №3
Решить задачу Коши:
 ;
;
 ,
, .
. ;
;
 ,
, .
. .
.
Решить граничную задачу:
5.
![]() .
.
6.
![]()
Вариант №4
Решить задачу Коши:
 .
. ;
;
 ,
, .
. .
.
Решить граничную задачу:
5.
![]() .
.
6.
![]() .
.
Вариант №5
Решить задачу Коши:
 .
. ;
;
 ,
, .
.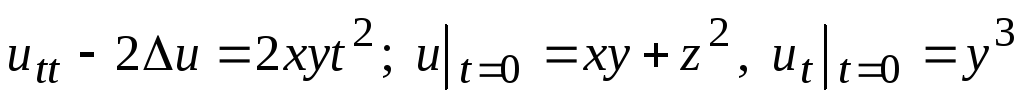 .
. ;
;
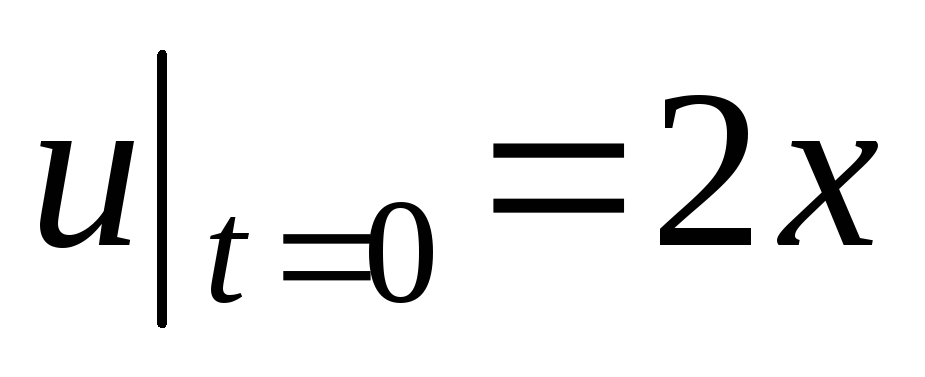 ,
, .
.
Решить граничную задачу:
5.
![]() .
.
6.
![]() .
.
Вариант №6
Решить задачу Коши:
 .
.
2.
![]() ;
;![]() ,
,![]() .
.
3.
![]() .
.
4.
![]() ;
;![]() ,
,![]() .
.
Решить граничную задачу:
5.
![]() .
.
6.![]()
Вариант №7
Решить задачу Коши:
1.
![]() .
.
2.
![]() ;
;![]() ,
,![]() .
.
3.
![]() .
.
4.
![]() .
.
Решить граничную задачу:
5.
![]() .
.
6.
![]()
Вариант №8
Решить задачу Коши:
1.
![]() ;
;![]() ,
,![]() .
.
2.
![]() ;
;![]() ,
,![]() .
.
3.
![]() .
.
4.
![]() .
.
Решить граничную задачу:
5.
![]() .
.
6.
![]()
Вариант №9
Решить задачу Коши:
1.
![]() .
.
2.
![]() ;
;![]() ,
,![]() .
.
3.
![]() .
.
4.
![]() ;
;![]() ,
,![]() .
.
Решить граничную задачу
5.![]()
6.
![]()
Вариант №10
Решить задачу Коши:
1.
![]() .
.
2.
![]() ;
;![]() ,
,![]() .
.
3.
![]() .
.
4.
![]()
Решить граничную задачу:
5.
![]()
6.
![]()
IV. УРАВНЕНИЯ ПАРАБОЛИЧЕСКОГО ТИПА
Вариант №1
Решить задачу Коши:
 ;
;
 .
. ;
; ;
;
 ;
;
Решить граничную задачу:
 ;
; .
.
Вариант №2
Решить задачу Коши:
 ;
;
 .
. .
. ;
;
Решить граничную задачу:
 .
.
5.
![]() .
.
Вариант №3
Решить задачу Коши:
 ;
;
 .
. .
.
 ;
;
Решить граничную задачу:
 .
.
Вариант №4
Решить задачу Коши:
 ;
;
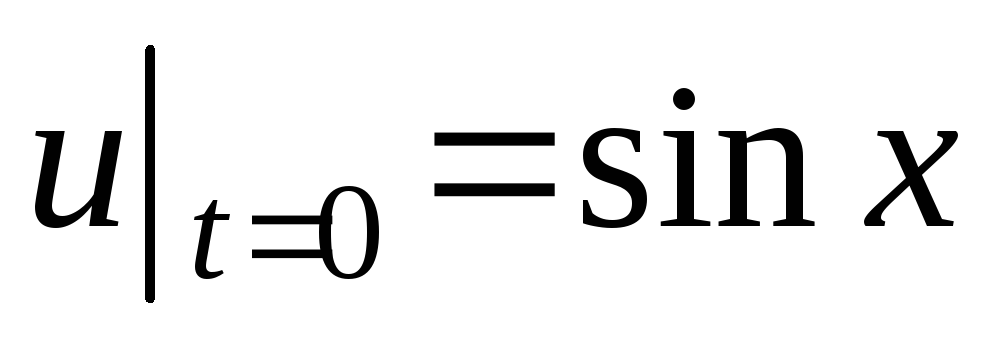 .
. .
. .
.
Решить граничную задачу:
 ;
;
Вариант №5
Решить задачу Коши:
 ;
;
 .
. .
. .
.
Решить граничную задачу:
 .
. .
.
Вариант №6
Решить задачу Коши:
1.
![]() ;
;![]() .
.
2.
![]() .
.
3.
![]() ;
;
Решить граничную задачу:
4.
![]() .
.
5.
![]() .
.
Вариант №7
Решить задачу Коши:
1.
![]() ;
;![]() .
.
2.
![]() .
.
3.
![]() .
.
Решить граничную задачу:
4.
![]() .
.
5.
![]() .
.
Вариант №8
Решить задачу Коши:
1.
![]() ;
;![]() .
.
2.
![]() .
.
3.
![]() ;
;
Решить граничную задачу:
4.
![]() .
.
5.
![]()
Вариант №9
Решить задачу Коши:
1.
![]() ;
;![]() .
.
2.
![]() .
.
3.
![]() ;
;
Решить граничную задачу:
4.
![]() .
.
5.
![]() .
.
Вариант №10
Решить задачу Коши:
1.
![]() ;
;![]() .
.
2.
![]() .
.
3.
![]() .
.
Решить граничную задачу:
4.
![]() .
.
5.
![]() .
.
V. УРАВНЕНИЯ ЭЛЛИПТИЧЕСКОГО ТИПА
Вариант №1
Найти функцию, гармоническую внутри единичного круга и такую, что
 ,
где:
,
где: .
.Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
 .
.Решить уравнение Лапласа в круге:
 .
.Решить уравнение Лапласа вне круга:
 .
.
Вариант №2
Найти функцию, гармоническую внутри единичного круга и такую, что
 ,
где:
,
где: .
.Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
 .
.Решить уравнение Лапласа вне круга:
 .
.Решить уравнение Лапласа в круге:
 .
.
Вариант №3
Найти функцию, гармоническую внутри единичного круга и такую, что
 ,
где:
,
где: .
.Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что

Решить уравнение Лапласа вне круга:
 .
.Решить уравнение Лапласа в круге:
 .
.
Вариант №4
Найти функцию, гармоническую внутри единичного круга и такую, что
 ,
где:
,
где: .
.Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что
 .
.Решить уравнение Лапласа в круге:
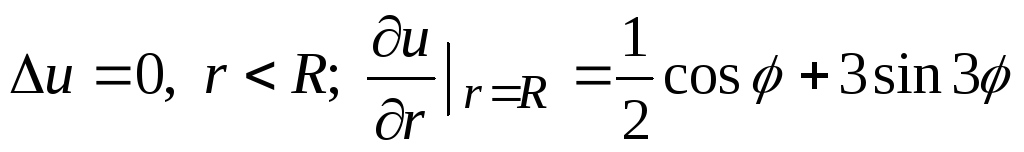 .
.Решить уравнение Лапласа вне круга:

Вариант №5
Найти функцию, гармоническую внутри единичного круга и такую, что
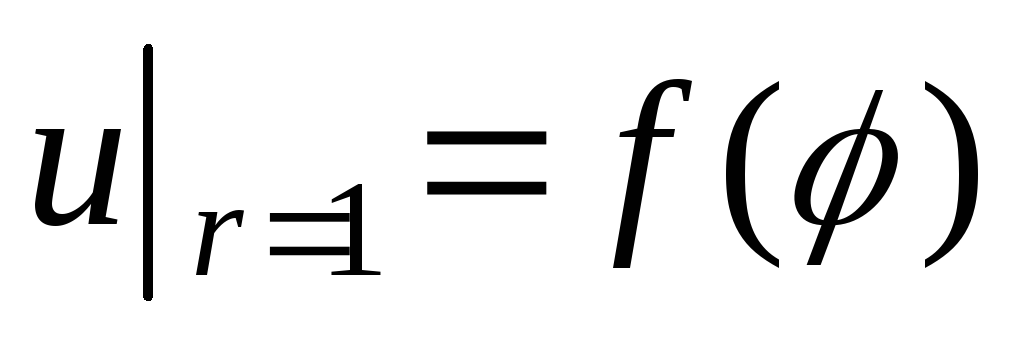 ,
где:
,
где: .
.Найти функцию, гармоническую внутри круга радиуса R c центром в начале координат и такую, что

Решить уравнение Лапласа в круге:
 .
.Решить уравнение Лапласа вне круга:
 .
.
Вариант №6
Решить краевую задачу для уравнения Лапласа в круге
1.
![]() .
.
2.
![]() .
.
Вариант №7
Решить краевую задачу для уравнения Лапласа в круге
1.
![]() .
.
2.
![]() .
.
Вариант №8
Решить краевую задачу для уравнения Лапласа в круге
1.![]() .
.
2.
![]() .
.
Вариант №9
Решить краевую задачу для уравнения Лапласа в круге
1.![]()
2.![]()
Вариант №10
Решить краевую задачу для уравнения Лапласа в круге
1.![]() .
.
2.
![]()
Список использованных источников
Тихонов, А.Н. и др Уравнения математической физики: Учебное пособие для университетов. / А.Н.Тихонов, А.А.Самарский - М.: Наука, 1977. – 735с.
Кошляков, Н.С. и др. Уравнения в частных производных математической физики: Учебное пособие для университетов. –М.: Высшая школа, 1970. –710с.
Мартинсон, Л.К. и др. Дифференциальные уравнения математической физики: Учебник для студентов вузов/ Л.К. Мартинсон, Малов Ю.И. Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1996.- (Сер. Математика в техническом университете; Вып. XII).
Сборник задач по уравнениям математической физики: Учебное пособие/ Под ред. В.С. Владимирова. –М.: Наука. 1974. –272с.
Курант Р. Уравнения с частными производными/ Под ред. О.А. Олейник. – М.: Мир, 1964. –832с.
Стеклов В.А. Основные задачи математической физики/ Под ред. В.С. Владимирова. –2-е изд. –М.: Наука. Главная редакция физико-математической литературы, 1983. –432с.
Михлин С.Г. Курс математической физики. –М.: Наука. Главная редакция физико-математической литературы, 1968. –576с.
Смирнов М.М. Задачи по уравнениям математической физики: Учебное пособие. –М.: Наука. Главная редакция физико-математической литературы, 1968. –112с.
