Архив2 / курсовая docx525 / Kursovaya (5)

Если вы еще и другое оформление используете, то я вообще буду премного благодарна

Я использую теорему Кронекера — Капелли (ТКК):

Если вы еще и другое оформление используете, то я вообще буду премного благодарна

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Вот оно решение:

Упростим расширенную матрицу АВ путем элементарных преобразований:

АВ=

Умножим 4-ую строку на (-1) и прибавим к ней 1-ую, одновременно с этим прибавим к 3-ей строке

1-ую, умноженную на (3), получим:

Умножим 4-ую строчку на () и прибавим получившуюся строку, умноженную на (-4), ко 2-ой строке и, умноженную на (-10), к 3-ей строке, получим:

Проведя те же элементарные преобразования с матрицей А, получим:

Рассмотрим минор 4-го порядка расширенной матрицы АВ:

= = (-1)*(β-4)* = -5(β-4)*(2-α)

• При β≠4 и α≠2 система будет несовместна, так как rang(AB)=4, а rang(A) ≤3 (по ТКК).

Рассмотрим 2 случая:

1. Случай. При 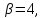то есть rang(AB)≤3

Так как при β=4 матрицу А путем элементарных преобразований, примененных к матрице АВ, можно привести к виду , рассмотрим минор 3-го порядка матриц АВ и А:

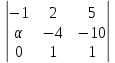
Прибавим ко 2-му столбцу 3-ий, умноженный на (-1), получим:

= = -6+3α = 3(α-2)

Рассмотрим 2 случая:

1. При β=4, α≠2 rang(AB) = rang(A)=3. Так как ранги матриц равны между собой и равны количеству неизвестных, то, по ТКК, система будет совместна и иметь единственное решение. Найдем это решение.

АВ:

Прибавим ко 2-ой строке 1-ую, умноженную на (2), получим:

Прибавим к 1-ой строке 3-ю, умноженную на (-5), а 2-ую строку умножим на (), получим:

Прибавим к 1-ой строке 2-ую, получим:

Умножим 1-ую строку на (--) и к 3-ей строке прибавим получившуюся 1-ую строку, умноженную на (-1), получим:

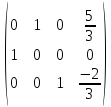
Следовательно,

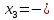
Проверка:

• Таким образом, при β=4, α≠2 система совместна и (0; ; 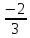) - ее решение

2. При β=4, α=2 rang(AB) = rang(A)≤2

Прибавим ко 2-ой строке 1-ую, умноженную на (2), получим:

Так как при β=4, α=2 матрицу А путем элементарных преобразований , примененных к матрице АВ, можно привести к виду , то рассмотрим минор 2-го порядка матриц А и АВ:

= -1 ≠0, значит, rang(AB)=rang(A)=2, но ранг больше числа неизвестных, следовательно, система будет иметь бесконечное число решений (по ТКК). Найдем эти решения.

АВ:

Прибавим к 1-ой строке 2-ую, умноженную на (-2), получим:

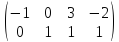
Следовательно, , , , где

Проверка:

• Таким образом, при β=4, α=2 система совместна и - ее решения

2. Случай. При то есть rang(AB)≤3

Прибавим ко 2-ой строчке 1-ую, умноженную на (-2), получим:

Так как при α=2 путем тех же самых элементарных преобразований можно привести матрицу А к виду , то рассмотрим минор 3-го порядка матриц А и АВ:

= (β-4)* = 4-β

1. При β=4 случай будет аналогичен случаю 1.2

2. При β≠4 rang(AB)=rang(A)=3 и ранг равен количеству неизвестных, то есть, по ТКК, система совместна и имеет единственное решение. Найдем это решение.

АВ:

Прибавим к 1-ой строке 3-ю, умноженную на (-2), а 2-ую строку умножим на(), получим:

Прибавим к 3-ей строке 2-ую, умноженную на(-1), получим:

Прибавим к 1-ой строке 3-ю, умноженную на (-3), и умножим получившуюся строку на (-1), получим:

Следовательно, , ,

Проверка:

• Таким образом, при α=2, β≠4 система совместна и (5; 0; 1) – ее решение

• При β≠4 и α≠2 система несовместна.

• При β=4, α≠2 система совместна и Х = (0; ; )

• При β=4, α=2 система совместна и Х =

• При α=2, β≠4 система совместна и Х = (5; 0; 1)