Интервальные оценки

При выборке малого объема точечная оценка неизвестного параметра может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом числе наблюдений следует пользоваться интервальными оценками.

Интервальной называют оценку, определяемую двумя числами – концами интервала, которые находят по известной величине выборочной характеристики. Интервальные характеристики позволяют установить точность и надежность оценок.

Пусть Θ^*оценка Θ неизвестного параметра генеральной совокупности. Вероятности, признанные достаточными для того, чтобы уверенно судить о параметрах генеральной совокупности на основании выборочных характеристик называются доверительными.

Надежностью (доверительной вероятностью) оценки Θ по Θ^*называется вероятность, с которой осуществляется неравенство:Θ-Θ^*или

Θ^*-ΘΘ^*+, т.е.Р(ΘΘ^*.

Интервал (Θ^*Θ^*), в котором с заданной доверительной вероятностью находится оцениваемый параметр генеральной совокупности называется доверительным интервалом,- точность оценки.

Обычно в качестве доверительных вероятностей выбирают значения 0.95, 0.99, 0.999.

Интервал является доверительным интервалом, в котором с вероятностьюнаходится математическое ожидание нормально распределенного признака Х генеральной совокупности, если среднее квадратическое отклонение признака Х неизвестно.

Интервал (_В^*(1-q);_B^*(1+q)) является доверительным интервалом для среднего квадратического отклонения генеральной совокупности.

Коэффициенты t_,qнаходятся по таблицам.

Используемая литература: [1-5,9,13,15,16,18-21].

Тема 4. Статистическая проверка статистических гипотез. Исследование статистических зависимостей

Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.

Проверяемую гипотезу обычно называют нулевой и обозначают .

На ряду с нулевой рассматривают альтернативную (конкурирующую) гипотезу .

Эти две гипотезы представляют собой две возможности выбора. Иных возможностей быть не может.

Алгоритм проверки статистической гипотезы :

1. по имеющейся выборке объема рассчитываем специально составленную характеристику;

2. по выборочному распределению определим критическое значение составленной характеристики такое, что, если гипотезаверна, то вероятность неравенстваочень мала;

3. Принцип практической уверенности: если вероятность события в данном испытании очень мала, то при однократном выполнении испытания можно быть уверенным в том, что событиене произойдет в практической деятельности и вести себя так, как будто событиеневозможно;

4. При гипотезаотвергается, пригипотезапринимается.

Правило, по которому гипотеза отвергается или принимается называетсястатистическим критерием. В названии критерия, как правило, содержится буква, которой обозначается специально составленная характеристика, рассчитываемая в критерии. В условия предыдущего алгоритма критерий назывался бы «-критерий».

Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона

Критерием согласия называют статистический критерий проверки нулевой гипотезы о предполагаемом законе неизвестного распределения.

В основе критерия согласия Пирсона лежит сравнение эмпирических (наблюдаемых) и теоретических частот наблюдений, вычисленных в предположении определенного закона распределения. Гипотеза здесь формулируется так: по исследуемому признаку генеральная совокупность распределена нормально.

Алгоритм проверки статистической гипотезы для критерияПирсона:

1. вычисляем выборочную среднюю и выборочное среднее квадратическое отклонение(смотри таблицу «Характеристики генеральной и выборочной совокупности» в разделе «Выборочный метод»);

2. по имеющейся выборке объема рассчитываем специально составленную характеристику, где– эмпирические частоты,– теоретические частоты,– объем выборки,– шаг (разность между двумя соседними вариантами),– нормализованные значения наблюдаемого признака,– табличная функция;

3. по выборочному распределению определим критическое значение составленной характеристики ;

4. При гипотеза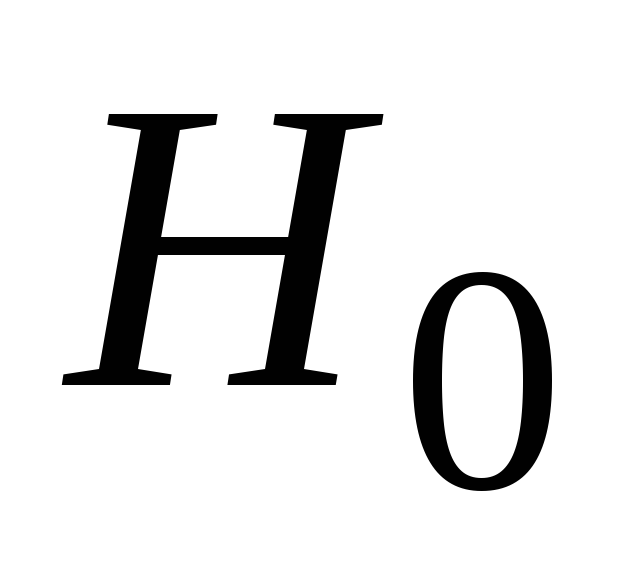отвергается, пригипотезапринимается.

Используемая литература: [1-5,9,13,15,16,18-21].