32Беседа 2. Конечные и бесконечные множества

Всамом деле, назовем весом дроби pq натуральное число |p| + |q|, т. е. сумму модулей ее числителя и знаменателя. Например, обе дроби

−32 и 14 имеют вес 5. Каждое рациональное число может быть пред- ставлено (и притом однозначно) в виде несократимой дроби с нату-

ральным знаменателем. Например, все дроби −23, −32, −46, −96 представ-

−2

ляют одно и то же рациональное число, но только дробь 3 дает

запись этого числа в виде несократимой дроби с натуральным знаме- нателем. Теперь будем последовательно нумеровать все несократимые дроби с натуральными знаменателями (т. е. рациональные числа), беря сначала дроби веса 1, затем дроби веса 2, веса 3 и т. д. Поскольку дробей каждого веса имеется лишь конечное число, мы постепенно перенумеруем все рациональные числа. Вот в какой последователь- ности они будут встречаться:

Этим и устанавливается, что множество всех рациональных чисел счетно.

Задачи и упражнения

11. Докажите, что множество всех рациональных точек на координатной плоскости (т. е. точек, у которых обе координаты рациональны) счетно.

12. Докажите, что множество окружностей, имеющих центры в рацио- нальных точках координатной плоскости и рациональные радиусы, счетно.

13. Докажите, что множество всех многочленов anxn + an−1xn−1 + ... + a1x + a0

данной степени n с рациональными коэффициентами счетно.

14. Фигуру на плоскости назовем «буквой Т», если она состоит из двух перпендикулярных отрезков, причем второй имеет один из концов в середине первого отрезка. Докажите, что любое бесконечное множество непересекаю- щихся «букв Т» на плоскости счетно.

ических чисел счетно.

10. Понятие мощности множества

Выше мы имели ряд примеров счетных множеств. Естественно возникает вопрос: все ли бесконечные множества счетны или же существуют несчетные множества? Ответ был дан Георгом Кантором. Он доказал, что множество R всех действительных чисел несчетно.

цифры). Таким образом, z не содержится среди чисел (5). Однако это противоречит тому, что среди чисел (5) имеются все действительные числа, заключенные между 0 и 1.

Мы видим, что предположение о счетности множества D при- водит к противоречию. Значит, это предположение ложно, т. е. мно- жество D несчетно. Поэтому и множество R всех действительных чисел несчетно.

Доказанная теорема послужила поводом для введения понятия мощности множества. Вспомним, что, рассматривая класс эквива- лентных между собой конечных множеств, мы с помощью абстракции отождествления приходим к понятию числа. Например, рассматривая множество всех ножек обычного стола и рассматривая всевозможные эквивалентные (т. е. содержащие столько же элементов) множества, мы приходим, абстрагируясь от всех конкретных свойств множеств и элементов, к понятию числа 4. Подобно этому для эквивалентных бесконечных множеств мы говорим, что у них одинаковая мощность (аналог «числа элементов»). Все счетные множества эквивалентны между собой, т. е. имеют одну и ту же мощность. Она обозначается,

согласно Кантору, символом 0; буква («алеф») — первая в древ-

нееврейском алфавите.

Мощность множества R всех действительных чисел обозначается готической буквой («цэ»); ее называют мощностью континуума (от латинского слова continuum — непрерывный). Согласно доказанной выше теореме Кантора, действительных чисел больше, чем элементов

любого счетного множества, т. е. > 0. В свою очередь, мощность0 больше мощности любого конечного множества: 0 > n для лю-

бого натурального n.

Заметим, что 0 — наименьшая бесконечная мощность. Это озна-

чает, что из любого бесконечного множества можно выбрать счетную часть, или, как говорят, счетное подмножество. В этом нетрудно убедиться. В самом деле, пусть M — бесконечное множество. Возьмем произвольный его элемент и обозначим его через a1. Так как множе-

ство M бесконечно, то кроме a1 в нем имеются еще элементы. Пусть a2 — один из них. Кроме a1 и a2 в множестве M имеются еще элементы (поскольку M бесконечно); обозначим через a3 какой-либо из них.

его подмножеством). Значит, множество M содержит не меньше эле- ментов, чем счетное множество M1, т. е. мощность множества М не

меньше 0.

Что же касается мощности континуума , то она не является «наибольшей» мощностью. Канторовский диагональный процесс (в несколько усложненной форме) позволяет доказать, что каково бы ни было бесконечное множество M, можно построить множество, ко- торое имеет еще большую мощность, чем М. Математики называют мощности также кардинальными числами. Это как бы «бесконечно большие» числа. Сказанное выше означает, что существует бесконечно много различных кардинальных чисел.

Весьма интересна связь мощностей с геометрическими понятиями. Для начала рассмотрим один софизм. Софизмом называют рассужде- ние, которое на первый взгляд выглядит вполне логичным и не вызывающим сомнения, тогда как вывод, к которому приводит это рассуждение, является явно абсурдным. Раскрыть софизм — значит указать ошибочное место в этом внешне логичном рассуждении и тем самым показать, почему это рассуждение приводит к абсурдному выводу.

Софизм, о котором идет речь, утверждает, что «все отрезки имеют одинаковую длину». В самом деле, возьмем два отрезка AB и CD, не равные между собой, и расположим их параллельно друг другу (рис. 29). Прямые AC и BD пересекаются в некоторой точке O. Теперь для любой точки X отрезка AB мы проведем прямую OX, которая пере- сечет второй отрезок в некоторой точке Y. Эту точку Y мы и поста-

вим в соответствие точке X AB. Этим устанавливается взаимно одно- значное соответствие между отрезками AB и CD, т. е. эти отрезки содержат одинаковое количество точек. Значит, они имеют одинаковую длину.

Раскрытие этого софизма несложно. Действительно, оба отрезка «содержат одинаковое количество точек», т. е. имеют одинаковую мощность. Однако мощность и длина — понятия разные, и из совпа- дения мощностей не вытекает равенство длин.

Заметим, что вся бесконечная прямая содержит «столько же» точек, сколько и любой отрезок. В самом деле, если отрезок изогнуть в виде дуги полуокружности с центром O (рис. 30), то центральное проектирование этой полуокружности из центра O на прямую, парал- лельную диаметру PQ полуокружности (рис. 31), устанавливает вза- имно однозначное соответствие между точками первоначального от- резка и всеми точками прямой. Правда, концы отрезка (или концы P, Q полуокружности) не поставлены в соответствие никаким точкам прямой, как видно из рис. 31, т. е. отрезок содержит «на две точки

больше», чем прямая. Однако это несуще- ственно, так как добавление к бесконеч- ному множеству конечного числа точек не изменяет его мощности. (Не может ли читатель доказать это?) Таким образом, любой отрезок имеет ту же мощность, что и прямая, т. е. мощность любого отрезка равна . Вообще, любая ломаная, любая окружность, любая ее дуга имеют мощ- ность .

Обратимся теперь к плоским фигурам. Кажется наглядно «оче- видным», что квадрат (или круг) содержит «больше» точек, чем от- резок. Однако это не так; здесь интуиция обманывает нас. Подобно тому, как рациональных точек на плоскости столько же, сколько рациональных точек на прямой (оба множества являются счетными), так и всех точек на плоскости «столько же», сколько и точек на прямой. Иными словами, мощность множества всех точек плоскости (или даже пространства) равна , т. е. совпадает с мощностью всех точек прямой.

Чтобы примирить читателя с его интуицией (которая, возможно, протестует против такой «несправедливости»), мы приведем канто- ровское доказательство того факта, что в квадрате «столько же» точек, сколько и в его стороне.

Рассмотрим на координатной плоскости квадрат с вершинами (0; 0), (1; 0), (0; 1), (1; 1) (рис. 32). Каждая точка M этого квадрата имеет две координаты x, y, причем каждая из этих координат пред- ставляет собой действительное число, принадлежащее отрезку [0; 1],

т. е. 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Это означает, что числа x, y могут быть записаны в виде бесконечных десятичных дробей:

(заметим, что мы всегда можем считать целую часть равной нулю, т. е. если x = 1, то мы можем написать x = 0,9999...). Теперь мы «пе- ремешаем» десятичные цифры чисел x и y, выписывая их поочередно, т. е. рассмотрим число

z = 0,a1b1a2b2a3b3 ...

Это число z мы и поставим в соответствие точке M квадрата (с ко-

ординатами x, y). Получается взаимно однозначное соответствие ме-

жду всеми точками квадрата и точками отрезка [0; 1]. Это показывает, что квадрат содержит «столько же» точек, сколько и отрезок, т. е. мощность квадрата равна . (Может ли читатель доказать, что в кубе «столько же» точек, сколько и в отрезке?)

Рассмотрим теперь вопрос о связи мощностей с неравенствами. Прежде всего уточним понятие подмножества. Мы говорим, что некоторое множество A является подмножеством множества M, если

каждый элемент множества A является также и элементом множества М. Это выражают записью A M. Заметим, что, согласно этому определению, само множество M является своим подмножеством: M M. Всякое же другое подмножество A множества M (т. е. такое, что в M найдется хотя бы один элемент, не принадлежащий A), называется собственным подмножеством множества M. В аристоте- левском постулате «часть меньше целого» под частью понимается именно собственное подмножество. На языке теории множеств арис- тотелевский постулат означает, что если A есть собственное подмно- жество множества M, то мощность множества A (т. е. число его элементов) меньше мощности множества M. Обозначая мощности

этих множеств готическими буквами («а») и («эм»), мы можем записать аристотелевский постулат неравенства:

Однако мы теперь знаем, что этот постулат верен лишь для конечных множеств.

В случае же бесконечных множеств из того, что A есть собственное

подмножество множества M, для их мощностей и вытекает лишь нестрогое неравенство

Примеры мы уже имели выше. Достаточно напомнить, что хотя мно- жество {2, 4, 6, ...} всех четных чисел является собственным подмно- жеством натурального ряда {1, 2, 3, ...}, но их мощности равны (оба

множества имеют мощность 0). Точно так же если отрезок PQ яв-

ляется собственным подмножеством отрезка AB, то из этого не сле- дует, что отрезок PQ имеет меньшую мощность: в самом деле, как мы знаем, оба отрезка имеют одну и ту же мощность 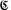. Таким обра- зом, в применении к бесконечным множествам аристотелевский прин- цип должен быть уточнен: часть (т. е. собственное подмножество)

множества M имеет либо меньшую, либо ту же самую мощность, что и целое (т. е. все множество M). Иными словами, при переходе от конечных множеств к бесконечным мы должны заменить аристоте- левское строгое неравенство (8) нестрогим неравенством (9).

Заметим, впрочем, что аристотелевский принцип «часть меньше целого» относится не только к числу элементов множества и его собственного подмножества («части»), но также к длинам отрезков, площадям фигур, объемам. О смысле аристотелевского постулата применительно к этим случаям мы еще будем иметь случай погово- рить в дальнейших беседах.

Задачи и упражнения

16. Докажите, что счастливых автобусных билетов (см. упр. 7) столько же, сколько билетов, у которых сумма цифр равна 27.

17. В языке племени Ододо всего два звука: «Д» и «О». Два слова обозначают одно и то же, если одно получается из другого при помощи