ной головы тут же вырастало пять новых. Еще голову срубит — опять на ее месте вырастает пять новых. Могло ли случиться, что в неко- торый момент битвы у Змея оказалась 2001 голова?

И здесь есть необходимый критерий: всегда число голов дает при делении на 4 остаток 3. А так как число 2001 не обладает этим свойством, то ни в какой момент битвы число голов у Змея не равнялось 2001.

78. Несколько слов о математической интуиции

Формирование навыков прогнозирования означает развитие ма- тематической интуиции и общей математической культуры. Человек с развитой математической интуицией быстрее и легче решает задачи, даже трудные, причем предлагаемые им решения чаще, чем у других, бывают необычными, красивыми. Математическая культура и интуи- ция предполагают наличие большого кругозора, умение по малей- шим, незаметным признакам находить аналогии с другими (иногда очень далекими) областями математики, умение легко усматривать новые формулировки задач на другом языке, находить различные модели задачи, видеть среди этих моделей более простые, более на- глядные. Интуиция — высшая ступень прогнозирования. Несколько примеров мы имели выше при разговоре о наглядности и аналогии. Ряд интересных дальнейших примеров можно найти в книгах «Как решить задачу», «Математика и правдоподобные рассуждения», «Ма- тематическое открытие», написанных американским математиком, выходцем из Венгрии, Д. Пойа.

Отметим еще один аспект, также тесно связанный с математичес- кой культурой и интуицией. Речь идет о том, чтобы выяснить, что значит свободно владеть некоторым математическим понятием. По мысли известного российского математика Д. К. Фаддеева, для хоро- шего владения математическим понятием недостаточно хорошо знать его определение и конгломерат основных теорем, в которых это понятие применяется. Существенным является также владение неко- торым достаточно богатым набором примеров, с разных сторон ил- люстрирующих смысл этого понятия. По существу, конечное число таких разнообразных примеров чаще всего заменяет нам формальное определение, влияет на глубину интуиции. Условимся в этом смысле говорить о фаддеевском наборе примеров, иллюстрирующих понятие.

Возьмем в качестве примера понятие коммутативной группы. Це- лые числа, группа из двух элементов (чет—нечет), вообще, группа вычетов по модулю p, затем рациональные числа, действительные числа, векторы ... Конечно, этот набор примеров является достаточно полным; он по-разному оттеняет понятие коммутативной группы (с точки зрения ее конечности или бесконечности, дискретности или непрерывности и т. п.). Но вот студент-математик познакомился с так называемыми p-адическими числами, совершенно не похожими по своим свойствам на перечисленные ранее примеры. Добавляя этот новый пример к своему фаддеевскому набору примеров коммутатив- ных групп, студент обогащает свое владение понятием коммутатив-

ная группа. Вообще, с каждой новой теоремой фаддеевский набор может увеличиться (оставаясь конечным). И если человеку с богатым набором примеров предложат вопрос «Верно или неверно такое-то утверждение о коммутативных группах?», он прежде всего сопоставит это утверждение с имеющимся в его распоряжении фаддеевским на- бором. И это также — важный элемент математической культуры и интуиции.

Интересным примером может служить построенный К. Вейер- штрассом пример непрерывной функции, которая ни в одной точке не имеет производной. Этот появившийся в XIX столетии пример существенно обогатил фаддеевский набор, относящийся к понятию «непрерывная функция». И другие теоремы Вейерштрасса (ограни- ченность непрерывной функции, заданной на отрезке; достижение наибольшего и наименьшего значений, свойство равномерной непре- рывности, возможность приближения непрерывных функций много- членами и др.) существенно обогащают относящийся к этому поня- тию фаддеевский набор. И несмотря на конечность таких наборов, связанных в сознании математика с каждым понятием, именно эти наборы составляют богатство нашего математического миросозерца- ния, именно они позволяют охватить мысленным взором дискретное и непрерывное в математике, определяют глубину интуиции как в самой математике, так и в ее приложениях.

К «фаддеевским наборам» относятся не только различные приме- ры объектов, принадлежащих к понятию, но также необходимые и достаточные признаки понятия вместе с относящимися сюда контр- примерами. Поясним это, взяв понятие «параллелограмм». Известен целый ряд свойств параллелограммов (т. е. необходимых признаков этого понятия): противоположные стороны параллелограмма конгру- энтны, противоположные углы конгруэнтны, диагонали делят друг друга пополам, биссектрисы противоположных углов параллелограм- ма параллельны и т. п. Можно отдельные необходимые признаки комбинировать и ставить вопрос о справедливости обратной теоре- мы, т. е. вопрос о том, является ли взятая комбинация достаточным признаком. Вот несколько примеров таких вопросов.

а) Является ли четырехугольник параллелограммом, если две его противоположные стороны параллельны, а две другие конгруэнтны?

б) Является ли четырехугольник параллелограммом, если у него стороны (не обязательно противоположные) попарно конгруэнтны?

в) Является ли четырехугольник параллелограммом, если у него одна из диагоналей делится другой диагональю пополам и, кроме того, две противоположные стороны конгруэнтны?

г) Является ли четырехугольник параллелограммом, если у него две биссектрисы углов параллельны и, кроме того, два противопо- ложных угла конгруэнтны?

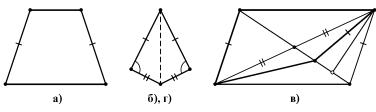
Все эти примеры нарочито подобраны так, что они имеют отри- цательный ответ, т. е. взятая комбинация необходимых признаков не является достаточным признаком. Контрпримеры приведены на

Рис. 458

рис. 458 (в контрпримере к вопросу г) биссектрисы даже совпадают). Эти контрпримеры обогащают смысл понятия «параллелограмм».

Вообще, не только типичные (или экзотические) примеры объек- тов, принадлежащих понятию, но и различные контрпримеры, отте- няющие смысл этого понятия (или, во всяком случае, навык постро- ения таких контрпримеров), составляют «фаддеевский набор», и чем он богаче, тем глубже наше владение рассматриваемым понятием. Большое количество контрпримеров собрано в книге Б. Гелбаума и Дж. Олмстеда «Контрпримеры в анализе».

Кроме указанных контрпримеров, показывающих, что некоторая комбинация необходимых признаков не составляет достаточного при- знака, важны и интересны также контрпримеры другого рода, от- теняющие условия теорем (в частности, необходимых признаков). Возьмем следующую хорошо известную теорему: если две противо- положные стороны четырехугольника параллельны и конгруэнтны, то этот четырехугольник — параллелограмм. Условие этой теоремы представляет собой конъюнкцию двух отдельных требований:

1) две противоположные стороны четырехугольника параллель-

ны;

2) эти же стороны конгруэнтны.

Попробуем выяснить, существенно ли для справедливости теоре- мы, что рассматриваются эти же противоположные стороны. Иными словами, не будет ли справедлива следующая теорема: если две про- тивоположные стороны четырехугольника параллельны, а две другие его противоположные стороны конгруэнтны, то этот четырехуголь- ник — параллелограмм? Равнобедренная трапеция является контр- примером, показывающим ложность этой гипотезы.

Вообще, если в условии некоторой теоремы имеется конъюнкция нескольких отдельных требований, то целесообразно выяснить, на- сколько существенным является каждое из этих требований, т. е. можно ли построить контрпример, отбросив одно требование. Более детально: если теорема имеет вид (> x) (A(x) B(x) C(x)) D(x), то

возникает вопрос, существует ли контрпример, показывающий суще- ственность требования A(x), т. e. контрпример, показывающий лож- ность теоремы (> x) (B(x) C(x)) D(x)? Иными словами, существу- ет ли x0, для которого B(x0) и C(x0) истинны, a D(x0) ложно?

Тот же вопрос о существенности ставится и в отношении требо- ваний B(x) и C(x). Такая работа (с каждой теоремой!) значительно повышает математическую культуру, кругозор и интуицию.