
- •Оглавление
- •Предисловие
- •1. Мнения о пользе математики
- •2. Понятия математики и их возникновение
- •3. Некоторые виды абстракции
- •4. Многоступенчатые абстракции
- •6. Количественные отношения реального мира
- •7. Множество и его элементы
- •8. Взаимно однозначное соответствие
- •10. Понятие мощности множества
- •Беседа 3. Операции над множествами
- •11. Пересечение множеств
- •12. Объединение множеств
- •13. Дополнение множеств
- •14. Произведение множеств
- •Беседа 4. Отображения
- •15. Общее понятие отображения и школьная математика
- •16. Некоторые виды отображений
- •17. Обратное отображение
- •18. Композиция отображений
- •19. Классификация
- •Беседа 5. Упорядоченные множества
- •20. Понятие упорядоченного множества
- •21. Минимальные элементы и математическая индукция
- •22. Трансфинитные числа и аксиома выбора
- •Глава 2. Комбинаторика
- •Беседа 6. Размещения, сочетания и родственные задачи
- •23. Размещения с повторениями
- •24. Системы счисления
- •25. Размещения без повторений
- •26. Сочетания без повторений
- •27. Сочетания с повторениями
- •28. Бином Ньютона
- •29. Производящие функции
- •30. Принцип Дирихле
- •Беседа 7. События и вероятности
- •31. События
- •32. Классическое понятие вероятности
- •33. Свойства вероятности
- •34. Условная вероятность
- •35. Независимые события и серии испытаний
- •Беседа 8. Случайные величины
- •37. Нормальное распределение
- •38. Закон больших чисел
- •Беседа 9. Информация
- •40. Количество двоичных цифр
- •41. Задачи на взвешивание
- •42. Понятие об энтропии
- •Беседа 10. Комбинаторные задачи о графах
- •43. Графы и их элементы
- •45. Плоские графы
- •46. Формула Декарта—Эйлера
- •47. Правильные многогранники и паркеты
- •49. Ориентированные графы
- •50. Конечные позиционные игры
- •51. Понятие о сетевом планировании
- •52. Существование и общность
- •53. Структура теоремы
- •54. Отрицание
- •55. Необходимое и достаточное условие
- •56. Конъюнкция и дизъюнкция
- •Беседа 12. Понятие об аксиоматическом методе
- •57. Возникновение аксиоматического метода в математике
- •58. Метрические пространства
- •59. Коммутативные группы
- •Беседа 13. Непротиворечивость, независимость, полнота
- •60. Непротиворечивость и понятие модели
- •61. Математические примеры моделей
- •62. Построение аксиоматики геометрии
- •63. Геометрия Лобачевского
- •64. Модель геометрии Лобачевского
- •65. Изоморфизм моделей
- •66. Полнота аксиоматики
- •67. Цикл озарения
- •68. Сфера достижимости
- •69. Анализ и синтез
- •70. Обратимый анализ
- •72. Поиск решения нестандартных задач
- •Беседа 15. Наглядность. Аналогия. Интуиция
- •74. Формула наглядности — изоморфизм плюс простота
- •75. Наглядность и математическая эстетика
- •76. Аналогия — общность аксиоматики
- •78. Несколько слов о математической интуиции
- •Решения задач и упражнений
- •Предметный указатель

306 |
Беседа 15. Наглядность. Аналогия. Интуиция |
|
|
Рис. 417 |
Рис. 418 |
Рис. 419 |
как ABK = KBC, то для доказательства равенства (*) достаточно |
||
установить, что |
|
|
|
1 = 4. |
(2) |
Возвращаемся к данным. Способа доказать равенство (2) пока не |
||
видно, но мы замечаем, что 1 равен другому углу: |
|
|
|
1 = A. |
(3) |
Возвращаемся к искомому. Из (3) видно теперь, что для подтверж-
дения соотношения (2) достаточно установить равенство |
|
A = 4. |
(4) |
Однако пока не видно, из чего можно было бы получить это равенство. Снова возвращаемся к данным. Замечаем, что A и 4 — острые углы прямоугольных треугольников ABC и DBC с общим острым углом C, т. е. A и 4 дополняют C до 90°:
A = 90° − C, 4 = 90° − C. |
(5) |
Значит, (4) верно (эврика!), чем и завершается решение.
Поиск решения проходил по схеме соединения анализа с синте- зом: движение шло попеременно в «прямом» и «попятном» направ- лениях, а инсайт осуществился в середине (рис. 419).
Заметим, что рассказ этого решения учащийся будет излагать не в том порядке шажков мысли, который реализован при решении, а в
виде синтетической цепочки (1) (5) (4) (3) (2) (*).
Беседа 15. Наглядность. Аналогия. Интуиция
74. Формула наглядности — изоморфизм плюс простота
Остановимся теперь на категории наглядности, которая имеет важнейшее значение для поиска решения задачи.
Понимание наглядности и ее роли в учебном процессе за послед- нее время значительно изменилось и расширилось. Мы сейчас счита- ем, что иной раз запись, сделанная мелом на доске, или даже устный рассказ учителя могут быть более наглядными, чем демонстрация явления в его натуральном виде. Например, формула серной кислоты,

74. Формула наглядности — изоморфизм плюс простота |
307 |
написанная на доске, является в некотором смысле существенно более наглядной, чем созерцание прозрачной жидкости (серной кислоты), налитой в сосуд, стоящий на столе учителя. Формула соединения говорит подготовленному учащемуся неизмеримо больше о химичес- ких свойствах соединения, чем натуральный объект: она вскрывает химический состав молекулы, валентные связи между отдельными атомами, позволяют легко найти молекулярную массу и т. п.
Разберем на этом примере, в чем заключается преимущество формальной записи соединения. Нас интересует лишь одна сторона явления: количество и характер атомов в молекуле вещества. От всех остальных сторон мы отвлекаемся, абстрагируемся. В этой модели отсутствуют все несущественные для нас стороны реального объекта. Модель отражает только одно — количество и характер атомов в химическом соединении. Это единственная сторона, связывающая нашу модель с реальным объектом. Но зато она представлена в рассматриваемой модели адекватно, изоморфно изучаемому явлению. В данном случае это означает, что реальная молекула и наша модель являются изоморфными по своему составу, а только состав нас в данном случае и интересует.
Итак, только одна сторона изучаемого явления отражена в моде- ли, причем отражена изоморфно, так что модель чрезвычайно упро- щает рассматриваемый процесс, огрубляет его. Взамен утраченных сторон явления модель приобретает простоту восприятия. Эти две характерные черты модели (изоморфное отражение существенных черт явления и простота восприятия модели) и выражают наглядность модели.
В этом смысле применяемые в школе модели геометрических тел являются наглядными. Например, понятие прямоугольного паралле- лепипеда, изучаемого в начальных классах, является довольно слож- ным. Оно предполагает умение абстрагироваться от цвета, поверх- ности тела, температуры, шероховатости и т. п., что дается учащимся далеко не сразу. Реальный предмет (например, деревянный брусок) не является, конечно, прямоугольным параллелепипедом в математи- ческом понимании, он служит лишь моделью. Эта модель изоморфно отражает основные свойства прямоугольного параллелепипеда как геометрического тела: у бруска столько же граней, ребер, вершин, сколько и у абстрактного параллелепипеда, такая же схема соедине- ния (например, в каждой вершине сходятся по три ребра). Таким образом, изоморфизм здесь налицо. В то же время деревянный бру- сок, несомненно, отличается простотой восприятия — предметы та- кого вида учащиеся неоднократно наблюдали, они для них просты и привычны. Мы видим, что модель прямоугольного параллелепипеда (так же как и модели других геометрических тел) обладает свойством наглядности.
Еще один пример. При изучении прямоугольного параллелепипе- да известную трудность для учащихся составляет понятие каркаса, т. е. фигуры, составленной из всех ребер и вершин параллелепипеда. «Увидеть» устройство этой фигуры, изучая деревянный брусок, не так

308 |
Беседа 15. Наглядность. Аналогия. Интуиция |
|
|
Рис. 420 |
Рис. 421 |
легко. Поэтому на уроках применяется каркасная модель прямоуголь- ного параллелепипеда (рис. 420). Изоморфизм здесь налицо (т. е. чи- сло вершин и ребер, а также схема соединения и параллельность на модели точно соответствует аналогичным элементам абстрактного каркаса). Неоспорима также и простота восприятия: невидимые ребра и вершины, которые ученику нелегко себе представить, рассматривая сплошной деревянный брусок, на этой модели хорошо видны; ясно видны четверки параллельных ребер, равенство противоположных ребер и т. п. Таким образом, каркасная модель оказывается (при изучении свойств параллелепипеда) проще для восприятия, чем сплошной деревянный брусок, а следовательно, и нагляднее.
Значение понятия изоморфизма как одной из двух существенных черт наглядности трудно переоценить. Требование правильного, аде- кватного отображения изучаемого явления с помощью прибора, таб- лицы и т. п. заключается в том, что это средство обучения должно представлять собой изоморфную модель. Благодаря этому выводы, полученные при рассмотрении модели, правильно, адекватно, изо- морфно отображают свойства самого изучаемого явления (в отноше- нии тех свойств реального явления, которые отображены в модели).
Простота модели, простота оперирования с ней означают, что с помощью модели проще придти к выводам (и притом к правильным выводам — в силу изоморфизма), чем при рассмотрении реального явления.
Переход к наглядной модели является важным средством решения математических задач, важным средством нахождения пути решения.
Можно пояснить применение наглядной модели следующим об- разом. Перед нами широкая река, один берег которой называется «первоначальной задачей», а второй — «наглядной моделью». Усло- вие задачи и поставленная цель нам понятны. Однако решение, т. е. переход от условия к поставленной цели по прямой представляет трудности. Можно представить себе, что дремучий, труднопроходи- мый лес встал на пути от условия к поставленной цели (рис. 421). Однако на другом берегу проложен существенно более простой путь, идущий как раз в нужном направлении. Это обеспечивается тем, что берега параллельны (т. е. наглядная модель изоморфна изучаемому явлению). Теперь для того, чтобы решить задачу, мы прежде всего переправляемся на другой берег, т. е. осуществляем действие модели- рования, как бы производим перевод тех данных, которые имеются в

74. Формула наглядности — изоморфизм плюс простота |
309 |
|
|
Рис. 422 |
Рис. 423 |
условии задачи, на язык терминов, имеющихся в наглядной модели. Благодаря простоте оперирования с наглядной моделью, мы значи- тельно легче, чем на берегу первоначальной задачи, продвигаемся шаг за шагом к достижению цели (т. е. выполняем учебные действия преобразования). Наконец, наступает инсайт: мы видим, что на Берегу наглядной модели мы подошли к решению, и требуется лишь пере- плыть реку, возвратиться на исходный берег, т. е. осуществить обрат- ный перевод (с языка наглядной модели к исходным терминам). Таким образом, при применении наглядности для решения задачи мы имеем три стадии решения:
1) моделирование, т. е. подбор подходящей наглядной модели и перевод первоначальной задачи на язык терминов этой модели;
2)оперирование с условием задачи на языке наглядной модели;
3)инсайт (Эврика! В этих терминах мы получаем требуемое ре- шение).
Рассмотрим некоторые примеры применения наглядных моделей при решении математических задач.
Пример 1. В выпуклом четырехугольнике точки M и N — сере- дины противоположных сторон AD и BC (рис. 422). Доказать, что
если MN = 12 (AB + CD), то ABCD — трапеция.
Заметим, что согласно хорошо известной школьной теореме, если ABCD — трапеция, то длина средней линии MN равна полусумме длин оснований. Задача состоит в том, чтобы доказать обратную теорему.
Для решения вместо точек будем рассматривать векторы. Это и есть та наглядная модель, которую мы здесь хотим применить. Вряд ли векторы проще для восприятия, чем точки (хотя векторная модель геометрии изоморфна обычной). Однако векторная модель все же обладает определенной простотой: оперировать с векторами легче, чем с точками, углами треугольника, поскольку с векторами можно производить действия (сложение, умножение на число), алгебраичес- кие свойства которых просты и привычны.
|
Итак, надо осуществить перевод условия задачи на язык→нагляд- |
ной модели, язык векторов. Для этого обозначим вектор MN через |
|
→ |
→ |
x |
и выберем такие направления отрезков чертежа, чтобы x был |
равен сумме получающихся векторов (рис. 423):

310 |
Беседа 15. Наглядность. Аналогия. Интуиция |
|
|||||
|
|
|
|||||
|
→ → → → |
(1) |
|||||
|
p |
+ |
s |
+ q = |
x , |
||
|
→ |
|
|
→ |
→ |
→ |
(2) |
|
(−p) + |
t |
+ (−q) |
= x . |
|||
Кроме того, по условию задачи |
|
|
|
||||
|
1 |
|
→ |
→ |
→ |
(3) |
|
|
2 |
(| s | + |
| t |) = |
| x |. |
|||
|
|
|
|
|
|
|
|
Этим осуществлен перевод задачи на векторный язык.
Перейдем теперь к преобразованиям в рамках нашей наглядной модели. Вид равенств (1) и (2) подсказывает, что их целесообразно сложить:
|
→ → |
→ |
|
|
|
(4) |
|
|
s + |
t = 2 x . |
|
|
|
||
Из равенств (3) и (4) получаем |
|
|
|
|
|
|
|
|
→ → |
→ |
→ |
+ |
|
→ |
(5) |
|
| s + t | = 2 | x | = | s | |
| t |. |
|||||
|
|
|
|
|
|
→ |
→ |
Отложим теперь от произвольной точки O вектор OE = s и от |
|||||||
→ |
→ |
→ |
→ → |
(рис. 424). Равенство (5) |
|||
точки E вектор EF = t . Тогда OF |
= s + |
t |
|
||||
показывает, что |
|
|
|
|
|
|
|
|
OF = OE + EF. |
|
|
|
(6) |
||
Теперь (эврика!) полученное равенство (6) означает, что E OF,
→ →
и потому s || t . Но это означает (если перевести это на геометри- ческий язык), что AB || CD, т. е. ABCD — трапеция.
Схема проведенного рассуждения показана на рис. 425, где двой- ная горизонтальная пунктирная прямая изображает «реку», разделяю- щую «Берег первоначальной задачи» и «Берег наглядной модели».
Использованная здесь наглядная модель (векторная интерпрета- ция геометрии) весьма полезна и очень часто применяется при реше- нии геометрических задач. Основная трудность при использовании этой наглядной модели состоит в том, чтобы удачно ввести обозна- чения нужных векторов, обеспечив тем самым перевод условия гео- метрической задачи на векторный язык.
Пример 2. Доказать теорему Архимеда: медианы произвольного треугольника пересекаются в одной точке (называемой центром тя-
Рис. 424 |
Рис. 425 |

74. Формула наглядности — изоморфизм плюс простота |
311 |
|
|
Рис. 426 Рис. 427 Рис. 428
жести треугольника), расстояние от которой до каждой вершины треугольника равно 23 длины соответствующей медианы.
Для решения обозначим через D середину стороны BC треуголь- ника ABC и введем векторы, как на рис. 426, где Q — произвольная
точка. Через M1 здесь обозначена такая точка, что AM1 = 23 AD. Это
— перевод задачи на векторный язык. Тогда
→ |
|
|
→ |
|
→ |
|
|
→ |
|
|
|
2 |
→ |
|
|
|
→ |
|
|
2 |
|
→ |
|
|
→ |
||||||
QM |
= QA |
+ AM |
= QA + |
3 |
AD |
= QA + |
|
3 |
(AQ + QD) = |
||||||||||||||||||||||
|
1 |
|
|
→ |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
+ |
|
2 |
|
|
→ |
|
|
|
|
→ |
|
1 |
→ |
|
2 |
→ |
= |
|
|||||||||
|
|
|
= QA |
|
3 |
|
(−QA |
+ QD) = |
3 |
QA + |
3 |
QD |
|
||||||||||||||||||
|
1 |
→ |
|
|
|
|
|
→ |
|
|
|
|
→ |
|
|
→ |
|
→ |
|
|
→ |
||||||||||
= |
|
2 |
|
1 |
|
+ |
1 |
|
|
1 |
|
1 |
|
|
1 |
||||||||||||||||
3 |
QA + |
3 |
|
|
QB |
2 |
QC = |
3 |
QA + |
3 |
QB + |
3 |
QC. |
||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Аналогично точка M |
BE, |
для которой BM = 2 BE (рис. 427) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
удовлетворяет |
|
|
|
|
|
|
|
|
|
→ |
|
|
= |
1 |
→ |
|
|
|
1 |
→ |
|
|
|
1 |
→ |
|
|||||
|
условию QM |
|
3 |
QA + |
3 |
QB + |
3 |
QC. Точно так же |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
точка M CF, для которой |
CM = |
CF (рис. 428), |
удовлетворяет |
||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
||
→ |
|
= |
1 |
→ |
|
|
1 |
|
→ |
|
|
1 |
|
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
условию QM |
3 |
QA + |
3 |
QB + |
3 |
QC. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Но (эврика!) это означает, что M1 = M2 = M3 — это одна и та же |
|||||||||||||||||||||||||||||||
точка. Этим и доказано, что все три медианы пересекаются в одной |
||||||||||||
точке M. Из доказательства видно также, что центр тяжести опреде- |
||||||||||||
|
→ |
1 |
→ → |
→ |
|
|
|
|
|
|
|
|
ляется равенством QM = |
3 |
(QA + QB + QC), какова бы ни была то- |
||||||||||
чка Q. |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
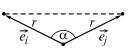
Пример 3. Вычислить радиус сферы, описанной вокруг правиль- |
|||||||||||
ного тетраэдра с ребром p. |
|
→ |
→ |
→ |
→ |
→ |
→ |
|||||
|
Для решения введем |
векторы |
||||||||||
→ |
e |
1 |
= OA, |
e |
2 |
= OB, |
e |
3 |
= OC, |
|||
→ |
|
|
|
|
|
|
|
|
||||
e4 |
= OD, где A, B, C, D — вершины правильного тетраэдра, а O — |
|||||||||||
центр его описанной сферы. Тогда
312 |
|
|
Беседа 15. Наглядность. Аналогия. Интуиция |
|
|
|
||||||||||||
|
||||||||||||||||||
OA = OB = OC = OD = r, AB = AC = AD = BC = BD = CD = p. |
||||||||||||||||||
Заметим теперь, что |
→ |
+ |
→ |
→ |
|
→ → |
|
|
|
|
||||||||
e1 |
e2 + |
e3 + |
e4 = |
0. Это вытекает из того, |
||||||||||||||
→ |
→ |
+ |
→ |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
||
что вектор e1 + |
e2 |
e3 + |
e4 |
|
не меняется ни при какой перестановке |
|||||||||||||
→ → → → |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
векторов e1, |
e2, e3, |
e4 |
(что возможно только в случае, если этот |
|||||||||||||||
|
|
|
|
|
вектор |
равен |
нулю). Возведя равенство |
|||||||||||
|
|
|
|
|
→ |
→ |
→ |
→ → |
|
|
|
|
|
|||||
|
|
|
|
|
e1 |
+ e2 |
+ e3 |
+ |
e4 |
= |
0 в квадрат, получим |
(учи- |
||||||
|
|
|
|
|
тывая, |
→ |
= r2, |
→ → |
= r2 cos α при i ≠ j, где |
|||||||||
|
|
|
|
|
что e 2 |
e |
e |
|||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
i |
j |
|
|
→ |
→ |
Рис. 429 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
α — величина угла между векторами ei |
и ej, |
||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
рис. 429) равенство 4r2 + 12r2 cos α = 0. Отсюда |
|||||||||||||
получаем cos α = − |
1. Следовательно, |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
→ → |
|
|
→ → |
|
|
|
|
|
|
2 r2 = |
8 r2, |
|
||||||
p2 = ( e |
− e )2 |
= 2r2 − 2 e |
i |
e = 2r2 − 2r2 cos α = 2 + |
|
|||||||||||||
i |
|
j |
|
|
|
|
j |
|
|
|
|
|
|
3 |
3 |
|
||
и потому r = |
√3 |
|
p. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2√2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Векторная модель является важным и широко применяемым сред- ством решения геометрических задач. Примеры использования этой модели были рассмотрены выше. Укажем еще одну наглядную мо- дель, которая также широко применяется при решении задач — на этот раз алгебраических. Этой моделью является графическое изобра- жение функций. Напомним построение этой модели подробнее.
Каждой числовой функции f соответствует ее график Γ(f ), т. е.
множество таких точек M(x; y) координатной плоскости, что x при- надлежит области определения функции f и выполнено равенство y = f(x). Сопоставляя каждой числовой функции f ее график Γ(f ), мы
получаем взаимно однозначное отображение Γ множества всех чис- ловых функций на совокупность всех подмножеств координатной плоскости, однозначно проектирующихся (параллельно оси ординат)
на ось абсцисс. Это отображение Γ является изоморфизмом в отно- шении ряда свойств.
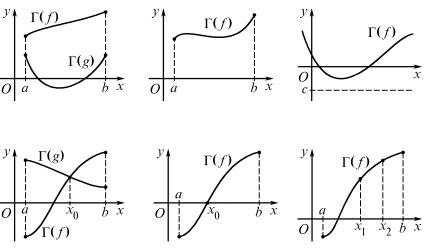
Перечислим несколько наиболее типичных свойств, которые лег- ко увидеть при помощи рассмотрения графиков.
1) На некотором промежутке выполняется неравенство f(x) > g(x); графически это выражается в том, что на рассматриваемом
промежутке график Γ(f ) расположен выше графика Γ(g) (рис. 430). Частным случаем является положительность функции f на некотором промежутке (ее график расположен на этом промежутке выше оси абсцисс, рис. 431). В качестве еще одного частного случая отметим, что если функция f ограничена снизу (т. е. существует константа c,
74. Формула наглядности — изоморфизм плюс простота |
313 |
|
|
Рис. 430 |
Рис. 431 |
Рис. 432 |
Рис. 433 |
Рис. 434 |
Рис. 435 |
удовлетворяющая условию f(x) > c для всех x из области определения функции f, то график Γ(f ) расположен выше некоторой горизонталь- ной прямой y = c, где c = const (рис. 432).
2) Число x0 является корнем уравнения f(x) = g(x), графически это
выражается в том, что графики Γ(f ) и Γ(g) имеют общую точку, абсцисса которой равна x0 (рис. 433). Частным случаем этого равен-
ства является утверждение о том, что x0 — нуль функции f, т. е. корень уравнения f(x) = 0; это означает, что точка A(x0; 0) принадле-
жит графику функции Γ(f ) (рис. 434).
3) Функция f является на некотором промежутке возрастающей, т. е. f(x2) > f(x1) при x2 > x1, где x1, x2 принадлежат рассматриваемому
промежутку; графически это выражается в том, что на данном промежутке при движении вправо график Γ(f ) поднимается вверх (рис. 435). Аналогично рассматриваются убывающие функции. Част- ным случаем этих свойств является достижение функцией f локально- го максимума (или минимума) в точке x0: если на некотором отрезке,
примыкающем к точке x0 слева, функция f является возрастающей, а на некотором отрезке, примыкающем к точке x0 справа, она является убывающей (рис. 436), то функция f достигает в точке x0 локального
максимума.
Имеются и другие свойства функций, наглядно выражаемые гео- метрическими свойствами их графиков, но указанные выше свойства являются наиболее часто применяемыми.

314 |
Беседа 15. Наглядность. Аналогия. Интуиция |
|
|
Рис. 436 Рис. 437
Хорошо сформированное «графическое мышление» заключается в умении использовать графики в качестве наглядной модели при решении задач (в частности, алгебраических).
Весьма важным является искусство обратного перевода. Напри- мер, парабола, являющаяся графиком функции y = ax2 + bx + c (где a ≠ 0), неограниченно уходит ветвями вверх при a > 0 и вниз при
a < 0. Надо уметь по эскизу графика (рис. 437) делать выводы о знаках коэффициентов a, b, c.
Приведем примеры решения задач при помощи описываемой на- глядной модели, т. е. посредством графиков функций.
Пример 4. Доказать, что если найдется число x = x0, при кото-
ром трехчлен x2 + px + q принимает отрицательное значение, то корни этого трехчлена действительны и различны.
Для решения заметим, что график трехчлена (парабола) имеет
ветви, направленные вверх (так как коэффициент при x2 положите- лен). График проходит через некоторую точку нижней полуплоскости (поскольку функция при некотором x принимает отрицательное зна- чение). Этим мы перевели задачу на язык наглядной модели. Теперь ясно, что этот график пересекает ось абсцисс в двух различных точках (рис. 438). Но это и означает (здесь мы осуществляем обратный пере- вод), что трехчлен имеет два различных действительных корня.
Можно предложить различные варианты рассмотренной задачи. Например, доказать, что при действительных a, b и отрицательном
c корни уравнения (x − a)(x − b) + c = 0 действительны и различны (это следует из того, что при x = a левая часть отрицательна). Или другой вариант: доказать, что если корни трехчлена x2 + px + q действитель-
ны и различны, |
то это же имеет место при q′ < q и для трехчлена |
x2 + px + q′. |
|
Пример 5. |
Доказать следующее утверждение: если квадратный |
трехчлен x2 + px + q принимает при x = a и при x = b отрицательные значения, то корни этого трехчлена действительны и удовлетворяют
условию |x2 − x1| ≥ |b − a|.
Для доказательства заметим, что график трехчлена имеет ветви, уходящие вверх, и заходит в нижнюю полуплоскость (поскольку трех- член принимает в некоторых точках отрицательные значения). Сле-
