8. Взаимно однозначное соответствие |
25 |
делится ни на одно из чисел p1, p2, ..., pk, что видно из его выражения
(4) (поскольку p1p2...pk делится на любое из чисел p1, p2, ..., pk, а после
прибавления единицы получается число, не делящееся ни на одно из них). Таким образом, остается единственная возможность: число n само является простым, т. е. совпадает с одним из чисел p1, p2, ...,
pk. Но это невозможно, поскольку, согласно (4), число n больше pk, т. е. больше каждого из чисел p1, p2, ..., pk. Итак, предположение о
том, что имеется лишь конечное число простых чисел, приводит к противоречию, т. е. это предположение должно быть отброшено как ложное. Значит, множество простых чисел является бесконечным.
Задачи и упражнения
1. Мадемуазель Рембо любит домашних животных. Известно, что у нее не менее трех животных. Все ее животные, кроме двух — собаки; все кроме двух — кошки; все кроме двух — попугаи; все, кроме собак, кошек и попугаев
— тараканы. Опишите множество животных у мадемуазель Рембо.
2. В люстре 5 лампочек. Переключатель имеет 6 положений, при которых горит разное количество лампочек: от 0 до 5. Однажды несколько лампочек перегорело. Может ли человек, не знающий схемы работы переключателя, определить множество перегоревших лампочек?
3. В комнате находятся 12 человек. Некоторые из них всегда говорят правду, а остальные всегда лгут. Каждый сказал по фразе. Первый сказал: «Здесь нет ни одного правдивого человека», второй: «Здесь не более одного правдивого человека», третий: «Здесь не более двух правдивых людей», и т. д., двенадцатый: «Здесь не более одиннадцати правдивых людей».
Определите, кто из них принадлежит множеству правдивых людей.
4. По полю проходит прямолинейная дорога. Человек, находящийся на дороге в точке A, может идти по полю со скоростью не больше 3 км/ч, а по дороге со скоростью не больше 6 км/ч. Определите множество точек, в которых он может оказаться через час.
5. На плоскости дан равносторонний треугольник ABC. Укажите множе- ство точек M, для которых оба треугольника ABM и ACM — равнобедрен- ные.
8. Взаимно однозначное соответствие
Студенты приехали на машинах копать картошку. Привезли и лопаты. Как узнать, хватит ли лопат? Конечно, можно пересчитать студентов и отдельно пересчитать лопаты. Но организаторы меро- приятия решили вопрос иначе. Они предложили студентам подходить по одному и брать лопаты. Очень быстро все лопаты были разобраны и их, по счастливой случайности, как раз хватило. Этим было уста- новлено, что студентов и лопат одинаковое количество. Как это было выяснено? Было установлено взаимно однозначное соответствие ме-
жду множеством студентов и множеством лопат. Это означает, что каждому элементу первого множества (студенту) был поставлен в соответствие один определенный элемент второго множества (лопата, которую взял этот студент), причем каждый элемент второго множе- ства (лопата) был поставлен в соответствие одному и только одному элементу первого множества.
26 |
Беседа 2. Конечные и бесконечные множества |
|
|
Рис. 17 |
Рис. 18 |
Рис. 19 |
Рис. 20 |
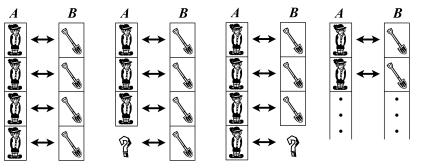
На рис. 17 схематически показано это взаимно однозначное соот- ветствие. Если бы был некоторый избыток лопат (рис. 18) или если бы некоторым студентам не хватило лопат (рис. 19), то взаимно однозначного соответствия не было бы. Возможность установления взаимно однозначного соответствия между элементами двух мно- жеств означает, что в этих множествах «одинаково много» элементов. Такие множества называются эквивалентными.
Вот другой пример. На танцплощадке собрались юноши и девуш- ки. Оркестр заиграл вальс, и юноши стали приглашать девушек на танец. Если окажется, что все пришедшие на танцплощадку распре- делились по парам, то этим будет установлено взаимно однозначное соответствие между множеством всех юношей и множеством всех девушек: каждому элементу первого множества (юноше) поставлен в соответствие в точности один элемент второго множества (девушка, которую он пригласил танцевать), причем каждый элемент второго множества поставлен в соответствие одному и только одному элемен- ту первого множества. Это соответствие показывает, что оба множе- ства эквивалентны, т. е. юношей присутствует столько же, сколько девушек.
Заметим, что каждый из нас многие тысячи раз устанавливает взаимно однозначное соответствие между множествами. Ребенок, трогая пальчиком один за другим разложенные перед ним предметы, производит пересчет, т. е. произносит «один», «два», «три», «четыре». Этим он устанавливает взаимно однозначное соответствие между множеством расположенных перед ним предметов и множеством {1, 2, 3, 4}, т. е. между заданным множеством предметов и отрезком натурального ряда, состоящим из нескольких первых натуральных чисел. Именно наличие универсального счетного множества, т. е. натурального ряда, позволяет сегодня ребенку легче постичь абстрак- цию числа. Число, названное последним (в данном случае «четыре»), отвечает на вопрос, сколько предметов (элементов) имеется в задан- ном множестве.
Натуральные числа позволяют сформировать первоначальное по- нятие «меньше» (или «больше»). Предположим, что мы пытаемся
8. Взаимно однозначное соответствие |
27 |
установить взаимно однозначное соответствие между двумя множе- ствами предметов, постепенно группируя их парами: «элемент из
A» ↔ «соответствующий элемент из B», «элемент из A» ↔ «элемент из B» и т. д. (рис. 20). Если при этом окажется, что мы исчерпали все элементы множества A, но в множестве B остались «лишние» элемен- ты (не поставленные в соответствие элементам из A, как на рис. 18), то мы говорим, что в множестве A меньше элементов, чем в B (а в множестве B больше элементов, чем в A). В этом случае установлено взаимно однозначное соответствие между множеством А и частью множества B. «Часть меньше целого», гласит один из принципов, выдвинутых великим древнегреческим мыслителем Аристотелем, со- здателем логики. А универсальное счетное множество (натуральный ряд) позволяет с помощью пересчета установить, в каком множестве меньше элементов, не группируя предметы парами (что было бы неудобно, если предметы громоздкие или тяжелые). Если при пере- счете оказалось, что в множестве A восемь элементов, а в множестве B — десять, то мы заключаем, что в А меньше элементов, чем в B, поскольку число 8 стоит в натуральном ряду раньше числа 10. И мы убеждены, что в этом случае можно установить взаимно однозначное соответствие между всем множеством A и частью множества B.
Все вышесказанное относится к конечным множествам. В древно- сти рассматривали почти исключительно конечные множества. По- строение бесконечного натурального ряда чисел и замечательное доказательство Евклида бесконечности множества простых чисел яв- ляются первыми прорывами в математику бесконечного.
Особенно характерно разграничение конечного и бесконечного в древнегреческой геометрии. Понятие «геометрического места точек», восходящее к Платону, является отголоском этого разграничения. Поскольку геометрическая точка имеет «нулевые» размеры, какое бы (конечное!) число точек мы ни «прикладывали» друг к другу, ничего, кроме точки, получиться не может. Поэтому, по мнению древнегре- ческих мыслителей, прямая (или окружность, или иная линия) не может «состоять» из точек, не может быть представлена как мно- жество точек, а есть лишь «место», где могут располагаться точки.
Евклиду (или его предшественникам — скорее всего, Евдоксу) принадлежит хорошо известная теорема, которую можно сформули- ровать следующим образом: множество всех
точек, равноудаленных от двух заданных точек |
|
А и B, есть прямая, перпендикулярная отрезку |
|
АB и проходящая через его середину (рис. 21). |
|
Иными словами, точка M в том и только в |
|
том случае одинаково удалена от точек A и B, |
|
если она расположена на указанном перпенди- |
|
куляре, и в этом смысле этот перпендикуляр |
|
есть «место» таких точек. Сегодня мы говорим, |
|
что прямая есть бесконечное множество точек |
Рис. 21 |
(и вообще любая геометрическая фигура есть
28 |
Беседа 2. Конечные и бесконечные множества |
некоторое множество точек), но древнегреческим ученым такая идео- логия была чужда.
Впервые перешагнуть пропасть между конечным и бесконечным попытался в XIX столетии чешский ученый Бернард Больцано. Имен- но он пришел к понятию взаимно однозначного соответствия. Но трудности, к которым вело это понятие применительно к бесконеч- ным множествам, остановили его. Несмотря на много интересных идей и результатов, содержавшихся в труде Б. Больцано (опублико- ванном лишь через много лет после его смерти), задача построения общей теории множеств им не была решена. Ее решение дал выдаю- щийся немецкий математик Георг Кантор. О трудностях, связанных с рассмотрением бесконечных множеств, которые обнаружил Больца- но и которые были преодолены Кантором, мы и поговорим в следу- ющем пункте.
Задачи и упражнения
6. На балу каждый кавалер станцевал ровно с тремя дамами, а каждая дама — ровно с тремя кавалерами. Докажите, что дам и кавалеров было поровну.
7. У кондуктора автобуса две катушки билетов: в одной билеты с номерами от 573000 до 573999, в другой — с номерами от 426000 до 426999. В какой из катушек больше «счастливых» билетов, т. е. таких, что сумма первых трех цифр номера билета равняется сумме следующих трех цифр?
8. На окружности отмечены 2001 белая точка и одна красная. Рассмотрим всевозможные многоугольники с вершинами в этих точках. Каких много- угольников будет больше — с красной точкой или без нее?
9. Число 222122111121 получается, если в некотором слове заменить буквы на их номера в русском алфавите. Какое это слово?
10. Имеется 3 синих и 5 красных палочек разной длины. Сумма длин синих палочек равна сумме длин красных. Можно ли распилить эти палочки так, чтобы их потом можно было расположить парами палочек равной длины и разного цвета?
9. Счетные множества
В одном театре было бесконечно много мест, и они были зануме- рованы натуральными числами: первое место, второе, ..., n-е место, ...
Соответственно и в гардеробе было бесконечно много крючков: № 1,
№2, № 3, ... Однажды на интересную премьеру все билеты были раскуплены, и в театр пришло бесконечно много зрителей: первый (т. е. обладатель билета на место № 1), второй, ... День был дождли- вый, все зрители пришли с зонтиками, которые они повесили в гар- деробе (в порядке самообслуживания) на соответствующие крючки: первый — на крючок № 1, второй зритель — на крючок № 2 и т. д. После спектакля, впопыхах, первый зритель взял зонтик с крючка
№2, второй зритель взял зонтик с крючка № 3, n-й зритель взял
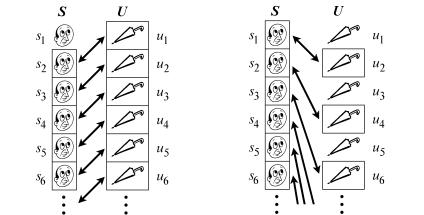
зонтик с крючка с номером (n + 1), ... (рис. 22). В результате все зрители ушли с зонтиками, но (к удивлению администрации этого бесконечного театра) на крючке № 1 остался «лишний» зонтик. Таким образом, если мы обозначим зрителей символами s1, s2, ..., а
9. Счетные множества |
29 |
|
|
Рис. 22 |
Рис. 23 |
зонтики — символами u1, u2, ..., то ситуацию можно описать следу-
ющим образом. Каждый зритель пришел со своим зонтиком, т. е. имелось взаимно однозначное соответствие между множеством
S = {s1, s2, ...} всех зрителей и множеством U = {u1, u2, ...} всех зонти-
ков (рис. 23). Однако после спектакля было установлено другое со- ответствие (рис. 22), при котором взаимно однозначно соответство-
вали друг другу множество S = {s1, s2, ...} и часть {u2, u3, ...} множества U всех зонтиков. Выходит, что часть {u2, u3, ...} множества
U всех зонтиков содержит «столько же» элементов, сколько и все множество U (поскольку каждое из этих множеств может быть при- ведено во взаимно однозначное соответствие с множеством S всех зрителей).
Это означает, что аристотелевский принцип «часть меньше цело- го», подмеченный при рассмотрении конечных множеств, рушится при переходе к бесконечным множествам. Вообще, в любом беско- нечном множестве M можно выбрать такую его часть Mi, (содержа-
щую не все элементы множества M), что существует взаимно одно- значное соответствие между M и Mi, т. е. между множеством и его
частью. Это — характерное отличие бесконечных множеств от конеч- ных. (Не захочет ли читатель попытаться доказать это утверждение?)
Прежде чем переходить к осмыслению этого факта, опишем со- бытия, которые происходили в этом «бесконечном» театре во время других спектаклей, чтобы лучше представить себе специфику беско- нечных множеств.
Во время одного из спектаклей также была дождливая погода, и все зрители пришли с зонтиками. Пока первый зритель беседовал с режиссером после спектакля, остальные забрали зонтики и ушли. При этом второй зритель взял зонтик № 1, третий зритель взял второй зонтик и т. д. (рис. 24). В результате первый зритель остался без зонтика! В один из дней (также дождливый) после спектакля первый
30 |
Беседа 2. Конечные и бесконечные множества |
|
|
Рис. 24 |
Рис. 25 |
зритель взял второй зонтик, второй взял четвертый зонтик, ..., n-й зритель взял зонтик с крючка с номером 2n, ... (рис. 25). В результате все ушли с зонтиками, но в гардеробе осталось бесконечно много зонтиков (а именно, зонтики с нечетными номерами).
На следующий день все пришли без зонтиков по случаю солнеч- ной погоды. Но за время спектакля погода испортилась, хлынул дождь. Однако администрация успокоила зрителей, сказав, что в гардеробе как раз имеется бесконечно много не востребованных вчера зонтиков. Значит, натуральный ряд как бы содержит «вдвое больше» элементов, чем всего в нем имеется...
Теперь читатель подготовлен к восприятию некоторых основных определений, связанных с бесконечными множествами. Как мы гово- рили, два множества называются эквивалентными, если между ними возможно установить взаимно однозначное соответствие. Если мно- жества P и Q эквивалентны, это вовсе не означает, что при любой попытке сгруппировать их элементы парами (один элемент из P и один элемент из Q, еще один элемент из P и еще один из Q и т. д.) мы непременно получим взаимно однозначное соответствие. Так, хотя в рассмотренном выше примере множества S и U эквивалентны (как показывает рис. 23), но изображенная на рис. 22 попытка сгруп- пировать элементы парами не приводит к установлению взаимно однозначного соответствия.
Однако наличие неудачных попыток ничего не означает. Если существует хотя бы один «удачный» способ, при котором устанавли- вается взаимно однозначное соответствие между рассматриваемыми множествами, то эти множества эквивалентны.
Каждое множество, эквивалентное натуральному ряду N = {1, 2, 3, ...}, называется счетным. Иными словами, множество M является счетным, если оно бесконечно, и при этом все его элементы можно
9. Счетные множества |
31 |
|
|
Рис. 26 |
Рис. 27 |
перенумеровать натуральными числами, т. е. записать это множество
в виде M = {m1, m2, m3, ...}.
Например, множество всех целых чисел (содержащее натуральные числа, нуль и отрицательные целые числа) является счетным. В самом деле, все целые числа встречаются в следующей последовательности:
0, 1, –1, 2, –2, 3, –3, ...
и теперь не представляет труда их все перенумеровать.
Несколько неожиданным является утверждение о том, что все целочисленные точки координатной плоскости (т. е. точки, у которых обе координаты являются целыми числами, рис. 26) также составляют счетное множество. Однако это становится понятным при рассмот- рении того способа нумерации, который показан на рис. 27: идя вдоль спиралевидной ломаной, мы последовательно встретим (и перенуме- руем) все целочисленные точки координатной плоскости.
Наконец, еще один пример. Целочисленные точки расположены на координатной прямой равномерно и изолированно (рис. 28). Ра-
p
циональные же числа, т. е. числа, представимые в виде дробей q с
целыми p, q (q ≠ 0), изображаются на координатной прямой всюду плотно, т. е. на любом отрезке, как бы мал он ни был, имеются рациональные точки.
Интуитивно кажется, что рациональных точек «существенно больше», чем целых. Во всяком случае целые числа составляют лишь часть множества всех рациональных чисел и, на первый взгляд, часть лишь «незначительную». Тем не менее, множество всех рациональных чисел счетно, т. е. их все можно перенумеровать натуральными чис- лами, и в этом смысле рациональных чисел столько же, сколько и целых (или натуральных).
Рис. 28